递推的贝叶斯估计方法

宁永成，侯代文

(91439 部队460 所，辽宁 大连 116041)

概率推理，研究如何利用带有噪声的观测信息，给出系统隐含的状态或者参数的最优一致估计的问题，是人工智能、自动控制、信号处理等领域的核心内容之一，在目标跟踪、语音识别、无线通信、惯性导航、神经网络训练以及经济预测等方面有着广泛的应用［1］。

递推的贝叶斯估计方法给出了解决这一问题的最佳方案，该方法每接收到一个新的观测量，就会递归地更新系统状态的后验概率密度函数(posteriori density function，pdf)，这一函数包含了概率推理问题的完整解决方案，能够给出系统状态的最优估计。然而，贝叶斯估计方法仅仅提供了状态估计的理论框架，在实际应用中，具体算法的选择依赖于系统状态、系统模型以及描述后验概率密度函数方法的具体形式。本文在简要介绍贝叶斯估计理论的基础上，在统一的框架之下，对各种状态估计算法进行归纳和总结，并对各自的使用方法、使用范围以及相互间的联系与区别，作了较为详细地阐述。

1 动态系统中的贝叶斯估计

本文将主要讨论离散时间的动态随机系统。用k=1，2，…，表示时间序列，k 时刻的系统状态用xk表示，假定系统状态是隐含的，无法直接得到，而只能在每个时刻得到含有噪声的观测值zk，目标是从观测序列中推导出系统状态中所需要的信息。以下部分，将用xn:m表示变量序列xn，xn+1，…，xn+m。

在贝叶斯框架下，系统状态及观测量之间的关系被融入概率密度函数p(x1:k，z1:k)中，由于p(x1:k，z1:k)= p(x1:k)p(z1:k|x1:k)，p(x1:k，z1:k)被进一步简化为2 部分，其中p(x1:k)表示系统的内部动态特性，p(z1:k|x1:k)表示测量噪声模型。这样，在给定观测序列z1:k后，利用系统的动态特性及测量噪声特性，就能够计算出系统状态的pdf p(x1:l|z1:k)，从而得到关于系统状态的有用信息。习惯上，当l ＞k 时，对应的问题称为预测问题;l=k 时，对应于滤波问题;l ＜k 时，对应于平滑问题。本文主要研究用于实时处理的滤波问题，对于平滑问题，可参阅文献［2-4］。

1.1 系统动态特性

对系统动态特性的描述，最简单的情况是作马尔科夫(Markov)假定，即系统状态xk仅与状态xk-1有关，而与k-1时刻之前的状态无关。此时

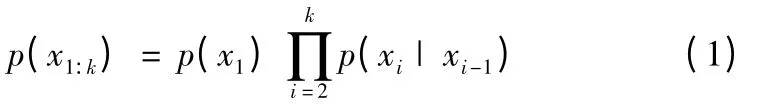
其中，p(x1)表示状态的先验概率密度函数。通常情况下，p(xi|xi-1)用系统状态方程来表示:

其中，vk-1表示k-1 时刻的过程噪声。隐马尔科夫模型(hidden markov model，HMM)［5-7］和卡尔曼滤波模型(kalman filter model，KFM)［8］是这一类模型的典型代表。

然而，有些系统并不遵循Markov 假定，即k 时刻的状态xk不仅与xk-1有关，还跟k-1 时刻前的状态有关。Neal［9］对这种比较复杂的系统进行了研究，这里不作详细讨论。

1.2 观测模型

一般情况下，观测量zk只跟当前状态xk有关，即

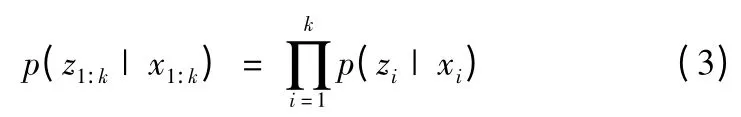
对于zk依赖于过去的观测序列z1:k-1的情况，从应用的角度讲，由于p(zk|xk)与p(zk|z1:k-1，xk)中都只有xk是自变量，二者没有实质性的差异［10］，不失一般性，仅讨论p(zk|xk)一种情况。

类似地，关系式p(zk|xk)用观测方程来表示:

其中，wk表示测量噪声。

1.3 递推的贝叶斯估计

贝叶斯估计是各种计算系统状态pdf p(x1:k|z1:k)方法的总称。p(x1:k|z1:k)描述了由观测序列z1:k推导的系统状态在状态空间上的分布情况，通过它可以精确求解系统状态在各种意义下的最优估计。利用贝叶斯法则，易知

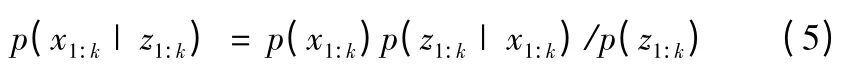
由于p(x1:k|z1:k)不能分解成更简单的形式，只能用非常复杂的模型来描述［11］;另一方面，对于实时处理问题，往往希望基于当前观测序列，得到当前状态的估计值，因此，一般情况下，更多地关注概率密度函数p(xk|z1:k)，而不是p(x1:k|z1:k)。

对满足式(1)的Markov 动态系统，求解p(xk|z1:k)可以利用上一时刻的估计结果，分2 步递归进行。首先，在获得观测量zk之前，利用k-1 时刻的观测序列z1:k-1以及状态估计值xk-1，预测状态xk的分布函数:

获得观测量以后，利用贝叶斯法则:

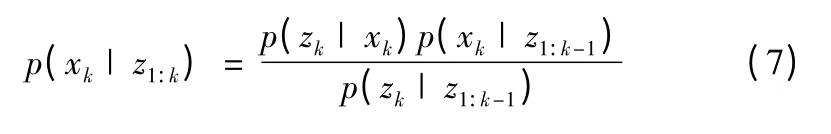
其中常数因子p(zk| z1:k-1)=∫p(zk| xk)p(xk| z1:k-1)dxk。当k=1 时，指定状态的预测分布等于先验概率分布p(x1)。利用式(6)、式(7)可以实现递推的贝叶斯估计。

然而，对大多数概率分布，式(6)、式(7)中的多维积分值都不能解析地求出，必须寻求pdf 的简单描述方式，才能使贝叶斯估计理论具有实际的应用价值。以下将根据对pdf 描述方式的不同，把贝叶斯估计方法分为参数化估计方法和非参数化估计方法两种类型，并分别介绍。

2 参数化估计方法

在理想条件下，pdf 可以用一组固定的参数集合λ 表示，即p(xk|z1:k)=p(xk，λk)，这时，滤波过程简化为由参数λk-1及观测量zk估计参数λk，KFM、HMM 就是2 种典型的参数化估计方法。

2.1 卡尔曼滤波(Kalman Filter，KF)［12］

由于均值和方差2 个参数概括了高斯分布的全部特性，如果滤波过程中，每一时刻的pdf 都是高斯型的，可以用参数集合λ={m，P}完整地表示该函数。这样，对pdf 的描述大大简化，使贝叶斯估计成为可能，KF 就是这一类估计方法。可以证明，若p(xk-1|z1:k-1)服从高斯分布，如果系统方程(2)、(4)满足以下条件，则p(xk|z1:k)也服从高斯分布:vk-1、wk也服从高斯分布，分别对应于方差Qk-1、Rk-1;函数fk(xk-1，vk-1)是xk-1、vk-1的线性函数;函数hk(xk，wk)是xk、wk的线性函数。

此时，动态方程(2)和观测方程(4)简化为

KF 算法的递推过程可描述为:

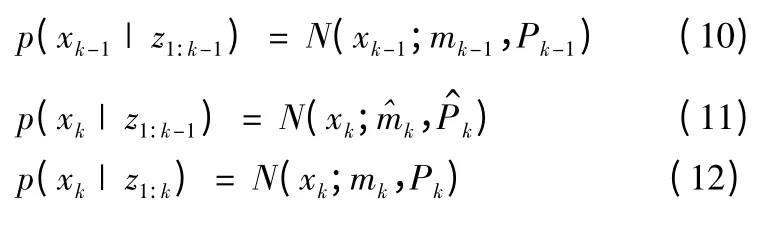
其中:

N(x;m，P)表示变量x 服从均值为m，方差为P 的高斯分布。

上述KF 方法对于满足条件的系统，能在最小均方误差意义下得到系统状态的最优估计。但是，在实际情况下，状态方程和观测方程往往是非线性的。对于f 和h 为非线性函数的情况，式(2)、式(4)不能再由式(8)、式(9)简单表示，只能用一些近似的线性化方法，把非线性函数转换为线型函数，然后利用线型滤波理论来处理。根据线性化方法的不同，这一类方法大致可分为扩展的卡尔曼滤波方法(extended KF，EKF)和sigma 点卡尔曼滤波(sigma-point KF，SPKF)方法2 种。

2.1.1 扩展的卡尔曼滤波

EKF 方法利用多维泰勒级数展开的一阶截短，对非线性函数围绕状态的当前估计值进行线性化，即对于非线性函数y=g(x)，作如下处理:

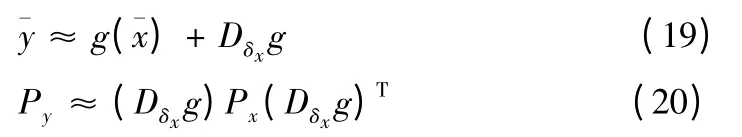
对于式(2)、(4)中f 和h 为非线性函数的情况，应用截短的泰勒级数展开，用代替KF 算法中的Fk，Hk，则非线性滤波问题转化为线性滤波问题，对应的算法就称为EKF 算法。

显然，式(18)中对高阶项的忽略，只有在零阶项、一阶项之和远大于其他高阶项时才能成立;而且，EKF 方法在线性化过程中，仅仅在状态的当前估计值这一点上作泰勒展开，而完全或略了随机变量x 的概率分布特性，这会对估计结果的一致性与准确性带来很大的影响，甚至导致滤波发散［13］。

2.1.2 sigma 点卡尔曼滤波

针对EKF 存在的缺陷，最近出现了一系列新的非线性滤波算法［14-17］，这些算法无论是理论基础还是实现形式，都显示出很大的优越性。Merwe［1］在统一的加权统计线性回归(weighted statistical linear regression，WSLR)［18］理论基础上，把它们归结为SPKF 方法。

WSLR 提供了一种对随机变量的非线性函数作线性化处理的有效方法，它通过在随机变量的先验分布上抽取r 个采样点，对每一个采样点作非线性转换，再对r 个转换值作线性回归，从而求得所需的均值和方差。由于WSLR 考虑了随机变量的概率分布特性，因而比泰勒展开方法误差更小。

对非线性函数y=g(x)，WSLR 需要在变量x 的分布上抽取r 个采样点χi，i=1，…，r，并作变换γi=g(χi)，定义:其中{wi}是r 个回归权值，满足

对应一个非线性函数，如何在随机变量的先验分布上选取采样点，也称sigma 点，以及如何确定各点对应的权值，成为一个关键问题。正是对这一问题的不同回答，导致产生无轨迹卡尔曼滤波(unscented kalman filter，UKF)［14］和中心差分卡尔曼滤波(central difference kalman filter，CDKF)［15，16］两种不同的滤波方法。

UKF 方法对sigma 点及对应权值的选取遵循以下原则:选取的sigma 点能够捕获随机变量x 最重要的统计特性，并把sigma 点的选取问题转化为以下的优化问题:

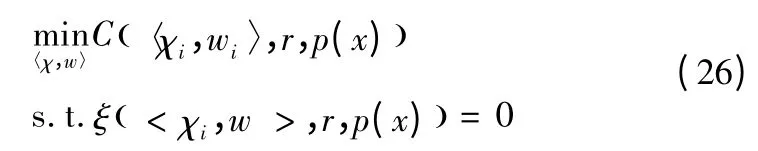
其中〈χi，wi〉是全部的sigma 点及其权值集合。函数ξ(·)表示约束条件，C(·)是代价函数，代价函数包含期望的统计特性，ξ(·)是必须满足的条件。在UKF 中，由于一阶、二阶矩是必须捕获得统计特性，约束条件可表示为

代价函数C(·)的确定视需要而定。如果要降低高阶矩的估计误差，则C(·)可选为ξ3(·)或ξ4(·);如果要尽可能减少sigma 点的数目，则C(·)=r。

基本的UKF 滤波方法常选取以下的sigma 点及其对应权值:

其中λ=α2( L+K)-L 是标度因子。α 决定sigma 点在周围的散布情况，β 为表明状态x 概率分布先验知识的参数。详细说明可参阅文献［19］。

由Ito 等提出的CDKF 方法，基于斯特灵(stirling)内插公式，利用中心插分代替式(18)中泰勒展开中的一阶、二阶级数。即令

当状态x 是多维向量时，通过线性变换作随机解耦，使各状态分量之间互不相关，从而把式(30)，式(31)扩展到多维的情况。

利用中心差分方法进行线性化时，sigma 点集及对应权值为

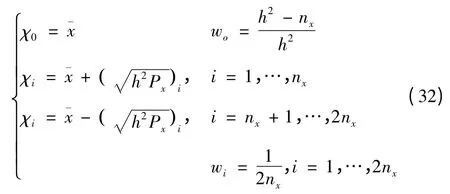
其中h 为区间长度参数，选择合适的h 能减少非线性变换后均值与方差的估计误差。可以证明［16］，当状态x 服从高斯分布时，

确 定 了 sigma 点 集 及 其 对 应 权 值 S ={( χi，wi)，i=1，…，r }以后，就得到SPKF 算法，由式(10)～式(12)及以下各式构成:

2.2 分布拟合滤波(Assumed-density Filter)［20］

除非特殊情况，如高斯分布、泊松分布，一般的概率密度函数难以用一组简单的参数准确表达。这时，常把真正的pdf p(xk|z1:k)投影到易于处理的概率分布q(x)上，即令p(xk|z1:k)=q(xk，λk)，其中λk为函数q(x)的参数，λk的选取应该使两函数p(x)、q(x)之间的Kullback-Leibler 距离最小，即

函数q(x)一般选作指数分布函数或者高斯分布函数，当q(x)选作一簇高斯分布函数的和，即选取λk= {(ai，mxk，i，Pxk，i)|i=1，…，M}时，对应的分布拟合算法就是高斯求和算法。此时

参数ai、mxk，i和Pxk，i确定以后，就可以通过M 个基本的卡尔曼滤波器并行滤波，对各自的状态估计加权求和，得到所需的状态估计值。在高斯求和滤波方法中，一个重要的问题是滤波过程中高斯混合项的个数随时间呈指数增长，如何有效地减少混合项的个数，使之保持在合理的数目内，成为该滤波方法的核心内容。基本方法包括舍弃混合项中权值较小的项;合并相似项等［3，23］。

2.3 隐马尔可夫模型［3，25，26］

当系统状态变量是离散值时，观测量与状态并不总是一一对应，而是通过一组概率分布相联系，这时需要用HMM 来描述该系统。HMM 是一个双重随机过程，包括描述状态转移的基本的Markov 链随机过程以及描述状态和观测量之间统计关系的随机过程。它可以由以下参数描述:N 为Markov链中状态的数目;M 为每个状态所对应的可能的观测量的数目;π 为初始状态概率向量，其中πi=P(x1=i)，1≤i≤N;A为状态转移概率矩阵，A = (aij)N×N，其中a ij = P(xi+1=j|xi=i)，1≤i，j≤N;B 为观测值概率矩阵，B=(bjk)N×M，其中bjl=P(zk=l|xk=j)，1≤j≤N，1≤k≤M。这样，可以记一个HMM 为η={N，M，π，A，B}。

同样，HMM 对pdf 的求解也可以进行参数化处理，即令p(x1:k|z1:k)=p(x1:k，λk)，其中λk=P(x1:k|z1:k，η)为随机向量，表示状态的离散分布。对HMM，在使用中需要解决以下3 个问题:

1)给定一个观测序列z1:k和模型η，在最佳意义上确定一个状态序列x1:k的问题，一般由递推的Viterbi 算法［27］解决。

2)给定一个观测序列z1:k和模型η，计算由模型η 产生出z1:k的概率，一般由前向—后向算法［28］求得。

3)给定一个观测序列z1:k时，确定模型参数η，使得P(z1:k|η)最大的问题。Baum-Welch 算法［26］利用递归的思想，使P(z1:k|η)局部最大，最后得到模型参数η。另外，用梯度方法也能达到类似目的。

3 非参数化估计方法—序贯蒙特卡罗(sequential monte carlo，SMC)

实际应用中，不是所有的pdf 都能用一组参数近似表示［24］;在某些情况下，特别是当状态x 维数较高时，难以得到积分式(5)的闭式解，这时需要寻求pdf 的其他表示方法。以SMC 为代表的新方法，不再寻求参数集合λ，而是用状态空间中的一组随机采样点，又称粒子，逼近pdf，这一类方法被称为非参数化方法。

SMC 基于随机模拟技术近似Markov 过程中难以处理的概率分布，尤其适用于状态连续且维数较高的系统。其核心思想是在任一时刻k，用N 个粒子及其相应重要性权值表示连续的pdf p(xk|z1:k)，并通过粒子及其权值计算状态估计值。当粒子个数趋于无穷大时，Monte Carlo 模拟的概率密度函数等价于pdf，相应的状态估计值接近于最优的贝叶斯估计。

设在k-1 时刻，pdf 近似为

其中δ(·)为冲激响应函数。利用上面的表达式，积分式(5)可以表示为

这样，贝叶斯估计中所有的连续函数的积分运算都由容易处理的离散求和形式代替，从而得到pdf 的估计为

SMC 方法在滤波过程中，粒子重要性权值的方差随时间持续增加，这使得滤波性能降低。经过几次递推后，将导致粒子集合中只有一个状态粒子的重要性权值较大，其余粒子权值为零，这种现象称为粒子多样性的丧失［1］。当有效粒子数目太小时，对pdf 的描述就不准确，甚至导致滤波发散。选取合适的重要性概率密度函数(importance density)或重采样方法，都能够降低由于粒子多样性丧失产生的粒子匮乏现象所造成的影响。

3.1 重要性概率密度函数的选取

实际应用中，先验性概率密度函数p(xk|xk-1)是使用最多的重要性概率密度函数，但它没有融入最新的观测量所包含的信息，导致重要性权值方差太大，从而不能准确描述pdf。Doucet 等［29］证明了最优的重要性概率密度函数能使重要性权值的方差最小，并指出其形式为

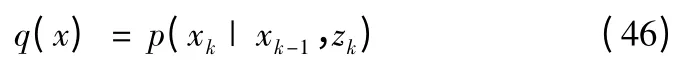
但是，在实际应用中，p(xk|xk-1，zk)的获取与直接从pdf 中抽取样本具有同样的难度，因而只能寻求次优的重要性概率密度函数。

扩展的卡尔曼粒子滤波器［30］(extended kalman particle filter，EKPF)，在k 时刻的观测量到达后，利用EKF 计算k-1时刻每一个粒子的在k 时刻对应的均值和方差，然后，以此均值和方差为基础，构造高斯分布函数作为新的重要性概率密度函数，并从这一函数中抽取相应的粒子。大量的应用［31］显示，该方法能改善粒子滤波器的性能。由于前面所述EKF 的缺陷，用SPKF 代替EKF 形成的新算法sigma 点粒子滤波器［17，32］(sigma-point particle filter，SPPF)具有更好的性能。

3.2 重采样

重采样方法提供了解决SMC 中，状态估计性能急剧下降问题的另外一种途径。它通过对粒子及其相应权值表示的概率密度函数选择性地重新采样，消除权值较低的粒子，增加权值较高的粒子个数。经常使用的重采样方法包括残差重采样(residual resampling)、系统重采样(systematic resampling)等［33，2］。

虽然重采样过程能在一定程度上降低滤波性能退化的问题，它同时也带来粒子来源路径的多样性降低，高权值粒子过分聚集的问题。平滑采样方法［34］(sampling smoothing method)通过给重采样后的粒子附加独立的偏差，以及增加采样前粒子的个数来缓解这一问题。其他的采样方法，也能改善滤波性能降低的问题，这些技术包括局部线性化方法、拒绝采样方法、辅助粒子滤波、内核平滑以及采用MCMC 等［30，33-37］。

3.3 计算量降低

SMC 的另外一个缺陷是当系统状态维数较高时，所需采样的粒子个数迅速增加，加大了滤波代价，同时降低了粒子的采样效率［38］。在有些情况下，状态变量可以分割为两部分，即xk=)，其中可以被解析地边缘化。这时，可以使用普通的滤波方法，如KF、HMM，对滤波，同时利用PF 对滤波，这一技术称为Rao-Blackwellisation［39］，它能够降低采样空间的维数，同时减少所需采样粒子的个数。

自适应粒子滤波器(adaptive particle filter，APF)［40］通过适时调整滤波中的粒子个数，也达到降低计算量的目的。APF 在滤波中，适时地计算粒子集合所表示的pdf 与真实的pdf 之间的Kullback-Leibler 距离，自适应地调整用于逼近pdf的粒子个数，在同样的滤波效果下，能够降低计算代价。

无论是Rao-Blackwellisation 方法还是APF 方法，在减少计算量的同时，都能够改善PF 中粒子枯竭的现象。

4 结束语

本文介绍了一系列概率推理方法的理论基础、应用条件及特点，并把它们统一于贝叶斯估计的框架之下。概括地讲，对于Markov 条件下的滤波问题，HMM 是离散状态估计的有效方法，KF 对线性、高斯条件下的连续状态估计提供了最优的解决方案，SMC 对非线性、非高斯问题的处理，显示出良好的应用前景。由于SMC 对问题的描述更接近问题的本源，它代表了贝叶斯估计未来的发展方向。

由于在认识、改造自然的过程中，经常会遇到隐含的、不确定性的问题，而概率推理方法，尤其是贝叶斯估计，提供了一部分问题的解决方案，贝叶斯估计方法正受到越来越广泛地关注，一系列重要的研究成果也在最近几年涌现出来。关于贝叶斯估计方法近期内可能的发展，主要有以下几个方向:

1)KF 框架在非线性较弱的条件下，仍不失为处理非线性问题的一种简洁、有效的方法。在线性化方法的选择上，除了传统的泰勒展开，最近发展的斯特灵插值，也可以考虑巴德(Padé)逼近方法，形成基于巴德逼近的新的SPKF 方法，因为对于相同阶数的多项式，巴德逼近具有更高的精度。

2)粒子滤波方法是当前研究的热点，结合其他滤波方法，提供更优的重要性概率密度函数;设计更优的重采样方法，减少重要性权值的方差，将继续成为今后的研究重点。

3)基于随机集合(Random set)理论的有限集合统计理论(finite set statistics，FISST)［41-44］，是贝叶斯估计理论的自然扩展，能够处理系统状态的维数随时间发生变化的贝叶斯估计问题，适用于处理多目标跟踪、定位与识别问题。特别是FISST 与SMC 方法的结合，是一个值得注意的研究方向。

［1］Merwe R V.Sigma-Point Kalman filters for probabilistic inference in dynamic state-space models［D］.USA:School of Science ＆ Engineering at Oregon Health ＆ Science University，2004.

［2］Kitagawa G.Monte Carlo filter and smoother for non-Gaussian nonlinear state space models［J］. Journal of Computational and Graphical Statistics，1996（5）:1-25.

［3］Kitagawa G.The two-filter formula for smoothing and an implementation of the Gaussian-sum smoother［J］.Annals Institute of Statistical Mathematics，1994，46（4）:605-623.

［4］Fong W，Doucet A，West M. Monte Carlo smoothing with application to audio signal enhancement［J］.IEEE Transactions on Signal Processing，2001.

［5］Martinerie F and Forster P.Data association and tracking using hidden Markov models and dynamic programming［C］//Proceedings of IEEE International Conference on Acoustic，Speech and Signal Processing.San Francisco，USA:IEEE，1992.

［6］Rabiner L R.A tutorial on hidden Markov models and selected applications in speech recognition［J］. Proc. IEEE，1989，77（2）:257-285.

［7］Rabiner L R，Juang B H.An introduction to hidden Markov models［J］.IEEE Acoustic，Speech，Signal Processing Magazine，1986:4-16.

［8］Kalman R E.A new approach to linear filtering and prediction problems［J］. Transactions of the ASME-Journal of Basic Engineering，1960:82（D）:35-45.

［9］Neal R. Markov chain sampling methods for Dirichlet process mixture models［J］. Journal of Computational and Graphical Statistics，2000:249-265.

［10］Saul L K，Jordan M I.Mixed memory Markov models: Decomposing complex stochastic processes as mixtures of simpler ones［J］.Machine Learning，1999，37（1）:75-87.

［11］Lerner U，Parr R.Inference in hybrid networks:Theoretical limits and practical algorithms［C］//Proc.of Uncertainty in Artificial Intelligence（UAI）.［S.l.］:［s.n.］，2001:310-318.

［12］Arulampalam M S，Maskell S.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking［J］.IEEE Transactions on Signal Processing，2002，50（2）:174-188.

［13］Wan E A，Merwe R.The unscented Kalman filter for nonlinear estimation［C］//In Proceedings of IEEE Symposium on Adaptive Systems for Signal Processing Communications and Control.Lake Louise Canada:IEEE，2000:153-158.

［14］Julier S J，Uhlmann J K.Unscented filtering and nonlinear estimation［J］. Proceeding of the IEEE，2004，92（3）:401-422.

［15］Ito K，Xiong K.Gaussian filters for nonlinear filtering problems［J］.IEEE Transactions on Automatic Control，2000，45（5）:910-927.

［16］Nørgaard M，Poulsen N，Ravn O.New developments in state estimation for nonlinear systems［J］. Automatica，2000（36）:1627-1638.

［17］Merwe R，Wan E A.Sigma-point Kalman filters for probabilistic inference in dynamic state-space models［C］//Proceedings of the Workshop on Advances in Machine Learning.Montreal，Canada，2003.

［18］Schei T S. A Finite-difference method for linearization in nonlinear estimation algorithms［J］. Automatica，1997，33（11）:2051-2058.

［19］西蒙·赫金.自适应滤波器原理［M］.郑宝玉，译.北京:电子工业出版社，2003:613-617.

［20］Minka T. A family of algorithms for approximate Bayesian inference［D］.USA:MIT Media Lab，MIT，2001.

［21］Alspach D L，Sorenson H W.Nonlinear Bayesian estimation using Gaussian sum approximations［J］.IEEE Transactions on Automatic Control，1972，17（4）:439-448.

［22］Sorenson H W，Alspach D L.Recursive Bayesian estimation using Gaussian sums［J］.Automatica，1971（7）:465-479.

［23］Cowell R G，Dawid A P，Sebastiani P.A comparison of sequential learning methods for incomplete data［J］.Bayesian Statistics，1996（5）:581-588.

［24］Murphy K.Dynamic Bayesian networks:Representation，inference and learning［D］. USA: University of California，Berkeley，CA，July 2002.

［25］Streit R L and Barrett R F. Frequency line tracking using hidden Markov models［J］.IEEE Transactions on Acoustic，Speech and Signal Processing，1990（38）:586-598.

［26］杨行峻 迟惠生.语音信号数字处理［M］.北京:电子工业出版社，1995:129-162.

［27］Forney G D. The Viterbi algorithm［J］. Proceeding IEEE，1973（61）:268-278.

［28］Baum L E，Egon J A.An inequality with applications to statistical estimation for probabilistic functions of a Markov process and to a model for ecology［J］.Bull.America Meteorol.Society，1967，73:360-363.

［29］Doucet A，Godsill S，Andrieu C.On sequential Monte Carlo sampling methods for Bayesian filtering［J］.Statistical Computation，2000，10（3）:197-208.

［30］de Freitas N，Niranjan M.Sequential Monte Carlo methods for optimization of neural network models［R］.CUED/F-INFENG/TR328，Department of Engineering，University of Cambridge，1998.

［31］Doucet A，Freitas N，Gordon N. Sequential Monte-Carlo methods in practice［M］.Springer-Verlag，2001.

［32］Liu J S，Chen R. Sequential Monte Carlo methods for dynamical systems［J］.Journal of American Statistics Association，1998（93）:1032-1044.

［33］Oudjane N，Musso C.Progressive correction for regularized particle filters information fusion［C］//Proceedings of the Third International Conference. FUSION 2000. Page（s）:THB2/10-THB2/17.

［34］Gordon N，Salmond D，Smith A F M. Novel approach to nonlinear and non-Gaussian Bayesian state estimation［C］//IEE Proceedings on Radar and Signal Processing.UK:IEE，1993，140:107-113.

［35］Doucet A，Gordon N. Efficient particle filters for tracking manoeuvering targets in clutter target tracking: Algorithms and applications［J］.IEE Colloquium，1999，11:4/1-4/5.

［36］Pitt M，Shephard Neil. Filtering via simulation: Auxiliary particle filters［J］.Journal of the American statistical Association，1999，94（446）:590-599.

［37］Andrieu Cand，Doucet A. Joint Bayesian model selection and estimation of noisy sinusoids via reversible jump MCMC Signal Processing［J］. IEEE Transactions on Acoustics，Speech，and Signal Processing，1999，47（10）:2667-2676.

［38］Arnaud Doucet_ Murphy N.Rao-Blackwellised particle filtering for dynamic Bayesian networks［C］//Proceedings of the 16th Conference on Uncertainty in Artificial Intelligence.［S.l.］:［s.n.］，176-183.

［39］Casella G. Rao-Blackwellisation of sampling schemes［J］.Biometrica，1996，83（1）:81-94.

［40］Fox D.KLD-sampling:Adaptive particle filters［J］.In Advances in Neural Information Processing Systems，2001（14）:713-720.

［41］Mahler R.Random sets:Unification and computation for information fusion—a retrospective assessment［C］//7th International Conference on Information Fusion. Stockholm，Sweden:FUSION，2004.

［42］Ba-Ngu Vo，Singh S，Doucet A. Sequential Monte Carlo methods for multi-target filtering with random finite sets［J］.IEEE Transactions on Aerospace and Electronic Systems，2005.

［43］Mahler R. Multitarget Bayes filtering via first-order multitarget moments［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39（4）:1152-1178.

［44］Vihola M.Random Set Particle Filter for Bearings-only multitarget tracking［C］//Proceedings of SPIE in Signal Processing，Sensor Fusion，and Target Recognition XIV.Orlando，Florida:Ivan Kadar，2005，301-312.