一种定周期控制下实现特定消谐调制的方法

宋鹏，王辉，金雪峰，姜一达，苏楠

（1.天津大学 电气与自动化工程学院，天津，300072； 2.天津电气传动设计研究所有限公司，天津 300180； 3.中石化管道储运分公司南京输油处，江苏 南京 210000；）

1 引言

采用PWM 调制的变流器装置，其开关损耗随 调制频率升高而增大，因此装置设计容量越大，调制频率也要相应降低，目前中压大功率应用中的开关频率一般在1 kHz 左右。降低开关频率可以提高 输出容量，但会导致输出电压谐波增加，严重时系 统无法正常工作。为了消除开关频率引起的谐波问题，研究人员提出了各种优化PWM 控制策略，特定谐波消除（specific harmonic elimination，SHE）是其中较为常用的一种[1]。

作为最早提出的PWM 方法之一[2]，特定消谐调制以消除某几个特定的低次谐波为目标，通过求解PWM 波形傅里叶级数展开式构成的超越方程组，得到一个周期内的开通、关断角度，实现调制脉冲输出[3-4]。和传统载波PWM 相比，在相同开关频率下，SHEPWM 得到的电压调制波形，其低次谐波较小，因此滤波器所需无功器件也较小，压缩了整个系统的成本和体积。

国内外学者关于SHEPWM 的研究，早期以求解非线性方程组为主[5-8]，近十年则以在各种功率变换器拓扑上的应用为主[9-12]。在已报导的文献中，关于如何实现在闭环控制中应用特定消谐调制的材料仍然较少。文献[13]介绍了SHEPWM 技术在“欧洲之星”高速列车上获得应用，但没有说明技术细节；文献[14]提出了一种补偿反馈信号中谐波电流的方法，使得闭环控制器不响应电流反馈信号中的谐波成分，生成正弦电压给定值给SHEPWM调制器。但该文献并未说明如何解决闭环控制运算周期较大、无法为SHEPWM 提供精确角度这一矛盾。文献[15]采用DSP 中断嵌套的方法实现了永磁同步电机矢量控制系统的SHEPWM 调制。主中断周期约为1.3 ms，用于实现矢量控制算法，其中嵌套一个50 μs 的高速中断，用于实现SHEPWM 的角度计算。但是该方法生成PWM 脉冲的查表操作是一个控制周期完成一次，这意味着电机低速运行时，SHEPWM 开关角度的误差可能较大，恶化控制性能。

本文介绍了一种在矢量闭环控制系统当中实现特定谐波消除调制（specific harmonic elimination PWM，SHEPWM）的方法，并将其应用于三电平中点钳位拓扑有源前端（three-lever NPC active front-end，下文简写为TLAFE）控制。采用矢量闭环控制算法算出电压给定矢量的幅值、角度和频率，以角度为初值对频率进行数值积分得到相对连续的角度，经单调处理后查表实现特定消谐脉冲输出。系统的控制器采用DSP + FPGA 构成主、从结构，矢量控制算法在DSP中实现，角度细化及SHEPWM输出等功能在FPGA 中实现，使得系统既可在较大的控制周期下完成矢量控制算法运算，也能以较高精度实现SHEPWM 脉冲生成。

2 特定消谐调制原理

图1以三电平AFE 输出的相电压波形为例说明SHEPWM 调制原理。

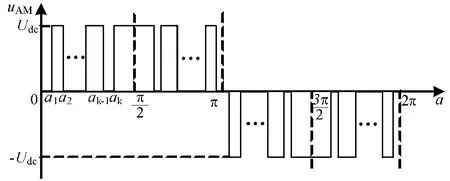
图1 TLAFE 相电压波形 Fig.1 Waveform of phase voltage of three-level AFE

图中，uAM为A相端子对直流侧中点M的电压，Udc为三电平的正组/负组直流电压。规定图1的波形为同步对称PWM，α是开关时刻对应的角度。k表示开关在1/4 周波内动作k次，图1所示为k是奇数的情况，也可以是偶数。求出1/4 周波内的开关角度αk即可实现调制，大于1/4 周波的情况可以根据对称性直接推出。

开关角度可以由期望的谐波含量求出。根据傅里叶变换原理，结合波形的对称性，图1波形的各阶谐波含量可写为

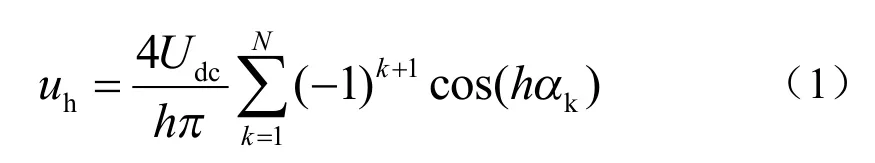
式中，uh为第h阶谐波电压，h为谐波阶数；N为1/4 周期内的开关次数；由于波形对原点中心对称，对α= π 轴线对称，不难推出傅里叶变换的直流分量和偶次谐波分量均为0，余下的奇次谐波分量中，3 的倍数次谐波在线电压中相互抵消，因此式（1）中h= 1，5，7，11，13，17，…。

式（1）实际上是关于cos（hαk）的线性方程组，若1/4 周期内开、关动作N次，则变量个数为N，可以消除N-1 个低次谐波。以N= 5，u1=uref，u5=u7=u11=u13= 0 为例，代入公式（1）可以得到方程组（2），其中uref为基波电压给定值。

由式（2）解出各开关角度即可实现SHE 调制，这一过程需反复迭代，在线计算难以保证控制实时性，通常采用查表调用实现。

3 有源前端矢量解耦控制

3.1 dq旋转坐标下TLAFE 数学模型

为简化分析，忽略电网内阻及线路阻抗，TLAFE 的主电路如图2所示。

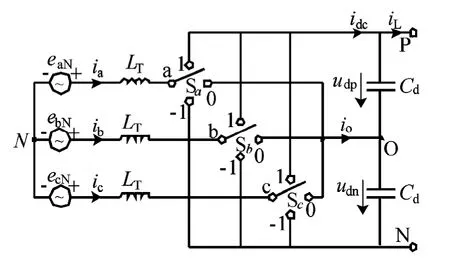
图2 TLAFE 主电路 Fig.2 Power circuit of TLAFE

图中，功率开关器件被等效为三通开关Sa、Sb、Sc，当三通开关分别处于1、0 和-1 3 个位置时，对应x相的相电压uxO分别为正组直流电压udp、0和负组直流电压的相反数-udn；N为网侧电压中性点，P、O 和N 分别为TLAFE 直流侧的正极、中点和负极；LT为滤波电抗，Cd为TLAFE 直流侧电容；exN、ix（x=a，b，c）分别为网侧相电压、相电流。

用开关函数σxi（x=a，b，c，i= 1，2，3）描述三通开关的3 种状态，即当Sx分别处在位置1、0 和-1 时，开关函数（σx1，σx2，σx3）的取值分别为（1，0，0）、（0，1，0）和（0，0，1）。考虑到在任意时刻

另外，考虑到网侧电压对称平衡且三相电流之和为0，可推导出基于开关函数描述的TLAFE 数学模型如下：

式中：下标x=a，b或c。

正、负组直流电容与三相电流的关系如下：

公式（3）～式（5）为采用开关函数描述的TLAFE 数学模型，该模型的推导过程物理意义明确，但由于网侧电压、电流为交流量，难以直接用于控制系统设计，因此通常对其应用dq旋转坐标变换，变换后的模型由三相变为两相、交流量变为直流量，形式有较大简化。

dq 旋转坐标变换公式如下：

式中，xdq，xabc分别为dq坐标系和abc坐标系下的向量，为坐标变换矩阵，且

式中：φ为dq坐标系超前abc坐标系的角度。

设网侧电压表达式为

对公式（3）～ 式（5）应用上述变换，得到

式中，ud=σd1udp-σd3udn，uq=σq1udp-σq3udn，分别为TLAFE 输出交流电压的d，q轴分量；ω= dθ/dt为dq坐标系旋转角频率，若选择坐标变换的角度φ与网侧a 相电压相角θ相等，则式（7）、式（8）中的ed=Em，eq= 0。式（7）、式（8）反映了TLAFE运行时的电压、电流关系，对式（9）、式（10）分别乘以udp，udn并相加，可以得到此时的有功功率传输关系。

式（7）～ 式（10）给出了TLAFE 系统的瞬时数学模型，实际控制系统设计时采用平均值模型，即在方程中用一个采样周期内的电压、电流平均值代替其瞬时值，这是后续传递函数推导及电压、电流控制器设计的基础。为方便推导，设定正、负组直流电压相等，简化的TLAFE 系统平均值数学模型如下：

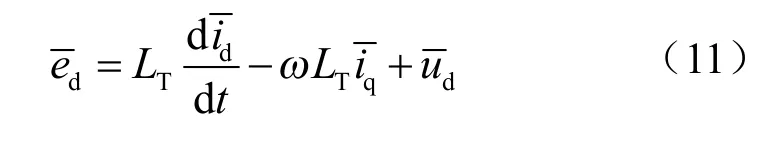
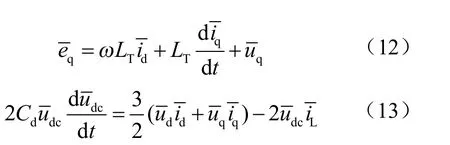
式中，上划线表示变量的平均值，在不致引起误解的情况下，后续公式中省略上划线；表示半组直流电压。可以看出，在正、负组直流电压平衡的前提下，三电平AFE 与两电平AFE 的数学模型完全一致。

3.2 电流闭环控制

式（7）～式（8）所示的电压电流方程中，d，q轴电流相互耦合，影响控制效果，采用前馈解耦控制可以实现解耦。当电流调节器为PI 调节器时，前馈解耦控制器设计如下：

式中：，为调节器输出的d，q轴电压参考值；，为d，q轴电流给定值；kpi，Ti为电流调节器比例系数和积分时间常数。

引入上述前馈控制，既去除了d，q轴电流之间的耦合，也使得PI 调节器只需承担对电流动态部分变化的调节，从而改善了调节器的动、静态响应。解耦之后的电流环框图如图3所示。

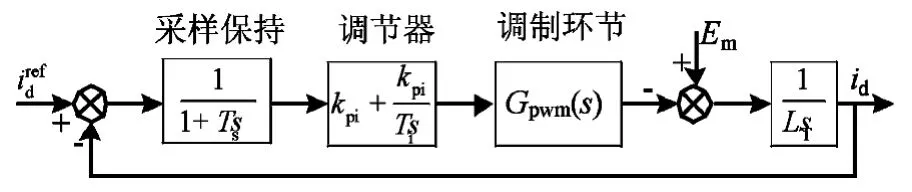
图3 电流环框图 Fig.3 Diagram of current control loop

图中，Ts为采样周期，Gpwm（s）为PWM 调制的传递函数，不同的PWM 调制方式对应的Gpwm（s）可能不同。对于异步调制，当前周期的PWM 电压平均值等于上一周期电压给定值（理想情况，即不考虑死时、功率器件压降等因素的影响），相当于一个延迟环节，由于延迟时间较小，可将其等效为一阶惯性环节。对于SHEPWM，PWM 电压的开关角度根据查表得到，当前周期的电压平均值不一定等于上一周期的电压给定，但是如果以较长的采样时间来平均，则实际电压平均值和电压给定较为接近。因此，本文将SHEPWM 等效为时间常数为2Ts的一阶惯性环节，大约是异步调制环节等效时间常数的2 倍，即

合并小时间常数的惯性环节，图3框图对应的开环传函为

为了兼顾电流环的抗扰性和快速响应能力，按照典型II 型系统整定PI 参数，取中频宽为hi=Ti/（3Ts）= 5，根据典型II 型系统参数设计关系得

按照上述方法整定出的调节器参数，其抗扰性能较好，但是电流超调较大，可以通过增设给定滤波器、微分反馈、微分调节器、复合控制等方法加以改进[17]。

3.3 电压闭环控制

由式（13）可以看出，AFE 的直流电压和其d，q轴电压、电流分量具有非线性关系（乘积），要实现对udc精确、快速的调节，需对模型做线性化处理[17]。但是，考虑到大多数应用中只需维持直流电压恒定，几乎不做调节或调节幅度很小，可以近似认为udc和id为线性关系，仍然采用线性PI 调节器作为电压控制器，传函框图如图4所示。

图4 电压环框图 Fig.4 Diagram of voltage control loop

图中，kpu，Tu为电压调节器比例系数和积分时间常数，Gc（s）为电流环闭环传函。由于和AFE数学模型存在差异，根据图4整定出的PI 参数在udc动态调节方面效果并不十分理想，但可有效维持直流电压恒定，因此其应用也较为广泛。

4 SHWPWM 实现方法

为了在矢量闭环控制系统当中实现SHEPWM 调制，本文采用DSP + FPGA 构成主、从结构的控制器，矢量控制算法在DSP 中实现，SHEPWM 生成在FPGA 中实现，使得系统既可在较大的控制周期下完成矢量控制算法运算，也能以较高精度实现SHEPWM 脉冲生成，系统的控制结构如图5所示。

图5 系统控制结构框图 Fig.5 Structure of the control system

基于图5所示的控制结构，实现SHEPWM 的步骤如下：

1）在DSP 中采用固定控制周期实现对PWM整流器的矢量解耦控制，得到给定电压的幅值Ur和角度θs，对θs求导可算出角度在上一周期内变化的平均频率Fr，然后将这些量传送至FPGA；

2）在FPGA 中，以接收到的给定电压角度作为初值，对频率做数值积分，得到相对连续的角度；

3）FPGA 根据单调处理后的角度及接收到的幅值，查表输出特定消谐PWM 脉冲；

上述步骤2）需要注意，稳态运行时，当前控制周期结束时刻积分得到的连续角度应和下一周期DSP 传至FPGA 的角度十分接近，每个控制周期初始时刻FPGA 的角度更新引起的角度变化不大。但在暂态时，给定电压的幅值、角度是根据闭环控制算法计算得出，相邻周期角度变化的频率可能不同，于是在控制周期开始时刻可能导致角度有较大的突增或突减，如图6所示。

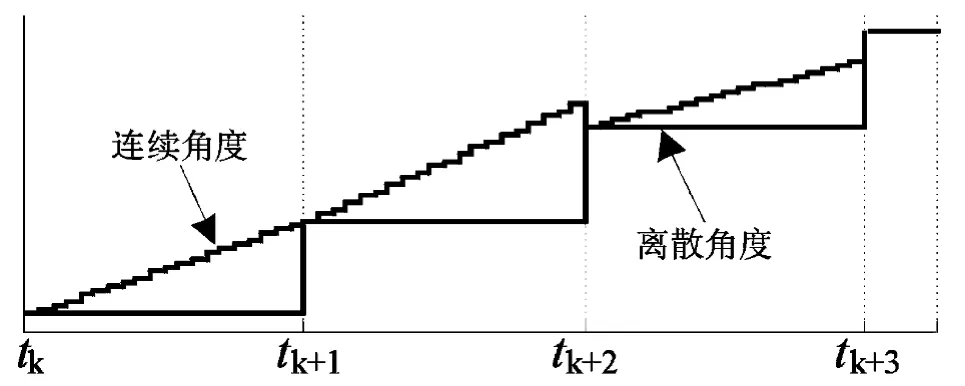
图6 角度突变示意 Fig.6 Schematic drawing for angle step changing

图6中tk～tk+1、tk+1～tk+2、tk+2～tk+3时间段分别为角度积分频率等于、大于、小于离散角度实际变化频率的情况，可以看到在tk+1、tk+2、tk+3时刻的连续角度分别等于、大于、小于离散角度，即用于生成SHEPWM 的角度在tk+2、tk+3时刻分别出现突减和突增。由于SHEPWM 脉冲是通过比较当前连续角度与存储在FPGA 中的开关角度实现，上述角度突减的现象可能使PWM 脉冲中出现窄脉冲，通过一些简单的逻辑将连续角度处理为单调递增变化即可抑制这一现象。考虑到电网电压频率变化很小，而相邻控制周期给定电压的角度突增幅度通常也不大，因此上述连续角度突增不太可能产生窄脉冲。

5 试验验证

所述方法在一台IGBT 三电平装置上做了试验验证。试验系统额定为：网侧线电压410 V，AFE 输出电流15 A，直流电压328 V。系统控制周期为700 μs，FPGA 中连续角度的积分运算频率为1 μs。特定消谐在1/4 调制波周期内的开关次数为7 次，可消除23 次以下的非3 倍数次特征谐波。

考虑到SHEPWM 输出波形中的低次谐波含量很小，但23、25 等高次谐波含量较大，可以将其滤波器设计为如图7所示的T 形结构，使得滤波器所需电感较小，且截止频率较高。

图7 T 形滤波器 Fig.7 T-type filter

图中，Lg= 1.9 mH 为网侧电感，La= 3.6 mH为AFE 侧电感，Cf= 14.4 μF 为滤波电容，Rf= 80.5 Ω 为滤波器阻尼电阻，Lf= 1.16 mH 为滤波电感，滤波支路谐振频率在1 200 Hz 左右，对24 阶及附近谐波抑制作用明显。实际上根据系统对稳定裕度、相移、谐波抑制效果及电感电容值的要求等约束条件的不同，上述参数取值并不唯一。关于SHEPWM 滤波器的设计可以作为一个专题研究，此处不再赘述。由于工频下Cf的容抗和Rf的阻值远大于Lg，La的感抗，建模时仍将其看做一个电感，即LT=La+Lg，因此第3 节的分析仍然适用。

图8给出了PWM 整流器突加100%负载时的暂态电流波形。

图8 突加负载暂态 Fig.8 Transient of impact load

图中，通道1 为网侧电流（10 A/格），通道2为AFE 电流（15 A/格），通道3、4 分别为正、负组直流电压（13 V/格，100%偏置显示）。可以看出，电流调节的上升时间大约30 ms，说明矢量解耦控制的动态响应较为迅速。

图9给出了稳态时的电流波形。

可以看出，网侧电流正弦度较好，但仍含有一些高频谐波，适当增大滤波器所用电感，尤其是AFE 侧电感能够有效抑制这些谐波。对图9波形的谐波分析结果表明，23 阶以下单次谐波含量不超过1%，23 次谐波含量较大，约为4%。和采用电感滤波的异步调制的试验结果相比，图9电流的高次谐波虽然较大，但低次谐波降低很多。

综合来看，以上试验结果说明所述方法具有较快的动态响应和较好的稳态谐波抑制能力。

6 结论

特定消谐调制能够消除PWM波形中的指定次数谐波，有助于抑制电力电子变换器的输出电流谐波，使其具有良好的稳态运行性能。特定消谐的消谐作用是针对于稳态情况，和传统的异步调制方式相比，其脉冲生成方式难以与闭环控制算法结合。另外，特定消谐PWM 环节的开关模式也难以用线性传函准确表达，给控制系统设计带来困难。本文尝试在闭环矢量控制系统中实现特定消谐调制，采用矢量闭环控制算法算出电压给定矢量的幅值、角度和频率，以角度为初值对频率进行数值积分得到相对连续的角度，经单调处理后查表实现特定消谐脉冲输出。所述方法在三电平AFE 试验样机系统上做了验证，结果表明系统兼具矢量控制的快速动态响应和特定消谐调制良好的稳态输出，在固定周期闭环控制系统中实现了特定消谐调制。

[1] 马小亮．高性能变频调速及其典型控制系统[M]．北京，机械工业出版社，2010．

[2] F.G.Turnbull.Selected Harmonic Reduction in Static DC-AC inverters[C]//.IEEE Trans.Communication and Electronics，83∶July 1964∶374-378.

[3] H.S.Patel and R.G.Hoft.Generalized Techniques of Harmonic Elimination and Voltage Control in Thyristor Inverters：PART I — Harmonic Elimination[J].IEEE Trans.Industry Applications，1973，IA-9(3)：310-317.

[4] H.S.Patel and R.G.Hoft.Generalized Techniques of Harmonic Elimination and Voltage Control in Thyristor Inverters：PART II — Voltage Control Techniques[J].IEEE Trans.Industry Applications，1974，IA-10（5），：666-673.

[5] Enjeti P.N，Lindsay J.F.Solving Nonlinear Equations of Harmonic Elimination PWM in Power Control[J].IEE Electronics Letters，1978，23（12）：656-657.

[6] T.Kato.Precise PWM waveform Analysis of Inverter for Selected Harmonic Elimination[C]// Industry Applications Society Annual Mtg，Denver，1986：611-616.

[7] 黄瀚，纪延超，张辉，等．优化特定消谐PWM 技术[J]．中国电机工程学报[J]，1997，17（5）：344-347．

[8] 佟为明，陈向阳，胡永烜，等．变频电源特定消谐技术中非线性方程组解法的研究[J]．中国电机工程学报，1998，18，（5）：357-360．

[9] Pontt J，Rodriguez J，Huerta R.Mitigation of Noneliminated Harmonics of SHEPWM Three-Level Multipulse Three-Phase Active Front end Converters with Low Switching Frequency for Meeting Standard IEEE-519-92[J].IEEE Trans.Power Electronics，2004，19（6）：1594-1600.

[10] Konstantinou G，Ciobotaru M，Agelidis V.Selective Harmonic Elimination Pulse-Width Modulation of Modular Multilevel Converters[J].IET Power Electronics，2013，6（1）：96-107.

[11] 费万民，吕征宇，姚文熙.三电平逆变器特定谐波消除脉宽调制方法的研究[J].中国电机工程学报，2003，23（9），：11-15．

[12] 李涛，张晓锋，乔鸣忠．NPC 逆变器特定谐波组消除法[J]．电气传动，2011，41（5）：25-30．

[13] Taufiq J.A.Advanced inverter drives for traction[C]//.Fifth European Conference on Power Electronics and Applications，1993，5∶224-228.

[14] Silva C，Oyarzún J.High Dinamic Control of a PWM Rectifier Using Harmonic Elimination[C]//.32nd Annual Conference on IEEE Industrial Electronics，2006：2569-2574.

[15] 郭新华，王永兴，赵峰，等．基于SHEPWM 的中压大功率牵引永磁同步电机两电平控制[J]．电工技术学 2012，27（11）：76-82．

[16] Blasko V.，Kaura V..A New Mathematical Model and Control of a Three-Phase AC-DC Voltage Source Converter[J].IEEE Trans on Power Electronics，1997，12(1)：116-123．

[17] 张兴．PWM 整理器及其控制策略的研究[D]．合肥：合肥工业大学，2003.