基于Chirplet变换和压缩感知的空中颤振目标稀疏成像*

徐艺萌,管 桦,王国正,张 群,周 丽

(1.空军工程大学信息与导航学院,西安710077;2.空军工程大学理学院,西安710051; 3.解放军94514部队,济南250002)

基于Chirplet变换和压缩感知的空中颤振目标稀疏成像*

徐艺萌1,**,管 桦1,王国正2,张 群1,周 丽3

(1.空军工程大学信息与导航学院,西安710077;2.空军工程大学理学院,西安710051; 3.解放军94514部队,济南250002)

针对在逆合成孔径雷达(ISAR)成像过程中目标非合作性机动导致的方位孔径稀疏现象与目标主体颤振引起的微多普勒效应相叠加对成像造成的影响,建立了颤振目标稀疏ISAR成像模型,分析了孔径稀疏和目标颤振对成像造成的影响,提出了一种基于Chirplet变换和压缩感知(CS)重构的成像方法,获得了颤振目标的高质量成像结果。仿真实验验证了该方法的有效性。

逆合成孔径雷达;颤振目标;微多普勒;稀疏孔径;线调频小波变换;压缩感知

1 引 言

逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)可以实现对运动目标的成像,为目标识别提供重要信息,在目标探测识别领域具有十分重要的应用价值[1]。在现代高动态战场环境中,雷达尤其是多功能雷达同时担负着目标搜索、跟踪、成像、识别等多重任务,每个任务所分配的系统资源是有限的。对目标进行成像时还需分出一部分固定的资源来实现对其他目标的搜索、跟踪及识别。此种工作模式下,雷达对各目标的观测时间通常是有限的、间断的。与此同时,由于目标的非合作性机动,往往会造成有限回波信号的缺失。两种因素结合导致出现方位孔径稀疏现象[2],影响成像质量。

当孔径缺失较少时,通常采用线性预测参数外推的参数化模型[3]或者现代谱估计[4]对目标实现成像;当孔径缺失较多时,有文献提出了基于压缩感知(Compressed Sensing,CS)的稀疏孔径成像方法,重构出了高质量的目标ISAR像[2]。然而,现代小型飞行器为了改善速度和操控性,设计时普遍采用细长机身+小展弦比大后掠机翼的机动构型,但是大后掠翼导致了飞行器的横向稳定性不佳[5],加重了飞行器整体结构出现的颤振现象(结构在高速气流中发生的一种自激振动现象,在超音速和高超音速飞行器上易发生[6]),特别是在目标进行非合作机动时(大攻角俯冲、大仰角攀升等),颤振现象会在一定的姿态角范围内对雷达的载波进行调制,产生含有周期性调制成分的雷达回波信号,这种现象被称为雷达目标的“微多普勒”效应[7],导致目标点在方位向上出现散焦,对成像造成污染。此种情况下,基于现代谱估计、线性预测参数外推、压缩感知的稀疏孔径成像方法难以取得理想的成像效果,因此有必要研究针对颤振目标稀疏ISAR成像方法。

从上述背景条件出发,本文提出了一种基于线调频小波(Chirplet)变换[8]。和压缩感知重构的颤振目标稀疏孔径ISAR成像方法。以线性调频信号为雷达发射信号形式,在对目标微动特性及横向稀疏特性分析的基础上,实现有效子孔径信号中微多普勒干扰信号的剔除,进而将全部有效子孔径中的微多普勒扰动剔除,并通过压缩感知从有效子孔径中恢复出全孔径信号,实现了颤振目标的稀疏ISAR成像。

2 颤振目标稀疏ISAR成像模型

雷达成像分析中,通常假设目标为散射点模型,这能给分析带来极大的方便[7-8]。本文建立目标平动散射点和颤振散射点在二维平面的运动模型。如图1所示,雷达固定于坐标原点O,目标中心初始位于x轴上的O′xref,y()ref点,以速度v沿y轴方向运动。目标中心到雷达的距离为Rref。目标由初始时刻位于坐标xm,y()m的m个平动散射点Pm和初始时刻分别位于坐标xn,y()n的n个振动散射点Pn构成,各振动散射点沿不同的定向轴以不同的最大振动幅度dnl、振动频率ωnl做周期性振动,则在某一时刻振动散射点的振动幅度为dnsin ωnl() t,定向轴在参考坐标系中的仰角为αnl。振动点中心位置C点初始坐标为xC,y()C。

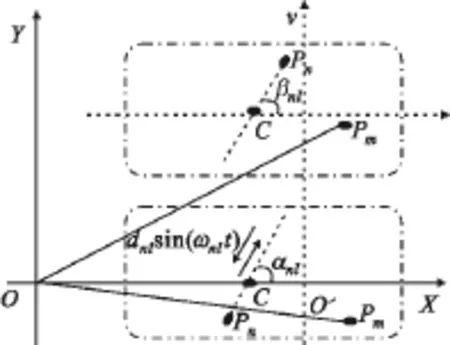
图1 雷达和含振动部件目标几何关系图Fig.1 The geometric diagram of radar and target with vibration part

假设雷达发射信号为线性调频信号:载频为fc,调频率为μ,脉冲宽度为Tp,当-1/2≤t≤1/2时, rect(t)=1。假设目标中心为参考点,对回波信号进行“dechirp”处理,然后以参考点的时间为基准进行快时间傅里叶变换,并去除剩余视频相位(RVP)和包络斜置项后[6],可得(基于“stop-go”近似模型):

其中:

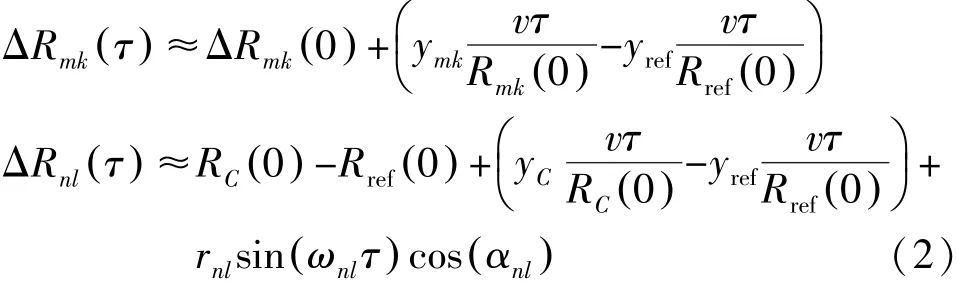
其中,σmk、σnl和Rmk(τ)、Rnl(τ)分别是第k个平动散射点和第l个振动散射点的反射系数和在慢时间τ距雷达的距离;c为光速;t为快时间;Tref是参考信号的持续时间;它比TP略大一些;RC(0)为初始时刻τ点到雷达距离;Rmk(0)表示初始时刻第k个平动散射点Pmk距雷达的距离。分别对平动散射点和振动散射点信号相位关于τ求导得

可见平动散射点信号在方位向是单频信号,因此对平动散射点信号在方位向做傅里叶变换,就能够得到对应散射点频率分量的峰值,而颤振散射点信号在方位向为正弦调制信号。已知式(1)的第二部分为dechirp处理后的振动散射点回波信号Svc(f,τ),对Svc(f,τ)相位项采用第一类Bessel函数展开,当Bessel阶数k大于[B+1]时Jk(B)≤10%忽略不计,进一步慢时间τ做傅里叶变换,得到

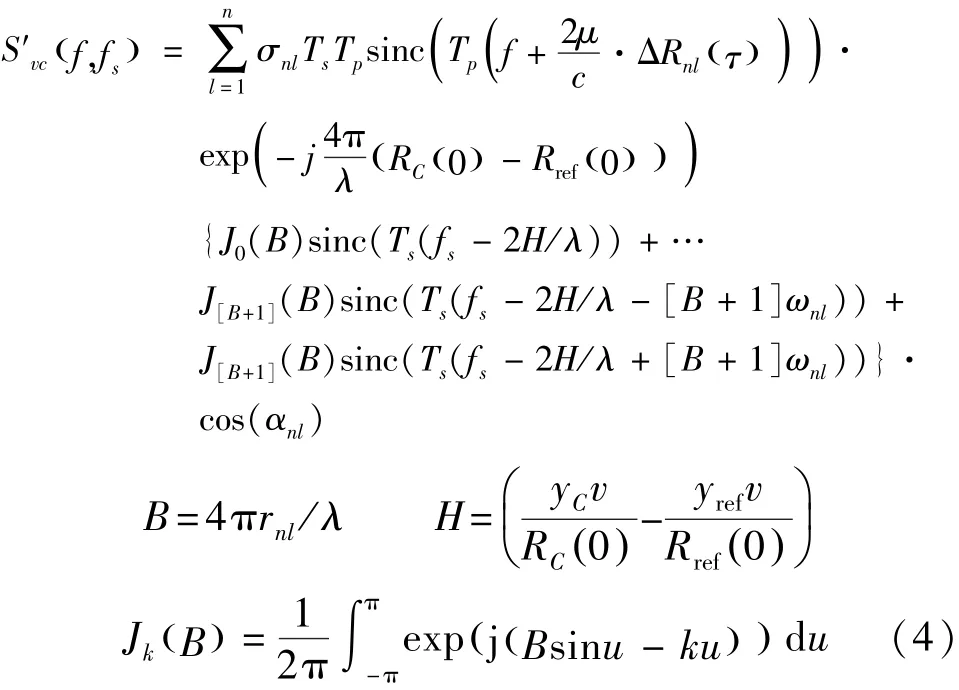
其中,B为微多普勒频率调制指数,Ts为方位向上的相干积累时间。上式诸多sinc函数中,2H/λ为由振动散射点相对雷达运动产生的方位向多普勒频率fn,因此振动散射点的回波信号在做方位向压缩时,将产生以fn为中心、以振动频率ωnl/2π为间隔的等间隔分布的无穷多对谱线上,设ρa为横向分辨率,在图像中将产生以Tsρaωnl/2π为间距的像元,可见振动散射点在方位向上造成散焦现象,并在目标的ISAR成像中产生干扰,且干扰程度随微多普勒调频率极值的增大而加强。

假设在ISAR成像时间内,为了获得一定的方位向分辨率,雷达共需要发射N个脉冲,但稀疏孔径ISAR成像条件下,由于回波信号的缺失,雷达只接收到了H段子孔径回波信号,共包括X次脉冲回波X＜()

N,如图2所示。

图2 目标回波信号示意图Fig.2 Echo signal of the target

假设第h( h=1,2,…,H)段子孔径中包含Nh次脉冲回波,这Nh次脉冲在总的N个脉冲中序号分别为hN1,hN2,…,hNh,τh=(hN1,hN2,…,hNh)/PRF, PRF为雷达脉冲重复频率,则平动散射点和振动散射点的方位向回波信号可分别写为

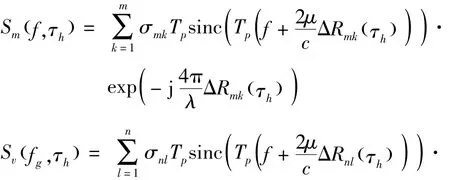
显然,由于孔径的缺失,直接对τh做傅里叶变换是无法有效实现方位向上的聚焦,即使对缺失孔径数据进行补零处理,方位向聚焦性能也是非常不理想的。

3 颤振目标稀疏成像算法

3.1 基于Chirplet变换的微多普勒信号分离

在颤振目标稀疏孔径ISAR成像中,对于每一段子孔径而言,运动补偿之后,平动散射点和振动散射点的方位向信号在较短的时间内可以近似为线性调频(LFM)信号。Chirplet变换是一种新的线性时频表示方式,可以理解为“是一段被窄窗函数抽取的线性调频波”[8-9]。当Chirplet具有光滑的高斯包络时,其基函数可以表示如下:

其中,σn、tn、ωn、βn分别表示Chirplet时间的宽度、时间中心、初始频率和调频率。原始信号s(t)可表示为一组Chirplet基gn(t)的线性叠加:

通过分析gn(t)的σn、tn、ωn、βn参数,就能够获得信号的特征。

在稀疏孔径ISAR成像中,从(f,τ)平面上抽取微动散射点所在距离单元的信号进行Chirplet分解后,我们能够将信号分解为一系列Chirplet原子之和。文献[9]对目标平动散射点和转动散射点进行了分析,它们的参数对(ωn,βn)分布在(ωn,βn)空间的椭圆上。

由于目标在运动过程中引起目标振动的原因呈现多样性,目标振动的频率范围较广,从几赫至几十千赫[10]。因此,本文对振动分两种情况来讨论。一种是ωnl/2π≈fn的条件下,一种是ωnl/2π≫fn的条件下。要实现振动散射点微多普勒信息的剔除,首先要确定动散射点相对雷达运动产生的方位向多普勒频率fn。由上文可以看出,fn与平动散射点相对雷达平动产生的方位向多普勒频率fm近似。平动散射点回波信号对应的Chirplet原子参数βnm模值的理论值为对式(1)相位部分关于慢时间τ求导数,由于平动散射点为单频信号,因此导数为零,故可以认为平动散射点回波信号对应的Chirplet原子参数βnm模值小于一极小的阈值βx。平动散射点回波信号对应的Chirplet原子参数ωnm的理论取值范围为

平动散射点回波的参数对(ωn,βn)分布如图3所示。假设发射信号载频fc=10 GHz,PRI=1/1000 s, Rref(0)=10 km,Rc(0)=9.95 km,Rmk(0)= 10.005 km,v=200 m/s,ymk=3 m,yref=1 m,yc=2 m。平动散射点回波信号对应的Chirplet原子参数ωnm的理论值范围为(-16.7 rad,+16.7 rad)。

图3 散射点Chirplet参数分布示意图Fig.3 The distribution of the Chirplet parameters of the scattering diagram

振动散射点回波信号对应的Chirplet原子参数βnv模值的理论值为对式(3)关于慢时间τ求导数:

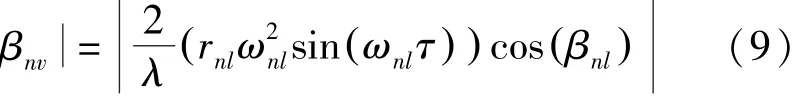
当βnv取最小模值0时,wn的模值为

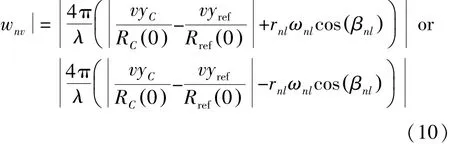
当ωnl/2π≈fn时,振动散射点回波振动部分对应的椭圆分布参数对(ωn,βn)与相对雷达运动部分fn的参数对(ωn,βn)分布如图3所示。βnv的模值最大值为βnv=cos( βnl)2rnlω2nl/λ,最小值为0,当βnv取最大值时,βnv≫βnm;当βnv取最小值时,由此可以看出,此时振动部分回波信号参数对(ωn,βn)的分布在βn轴方向范围相对平动部分差异性较大,如图3所示。因此可以通过设置βn的阈值βx有效实现振动部分的分离。当ωnl/2π≫fn时,振动散射点回波振动部分对应的椭圆分布参数对(ωn,βn)与相对雷达运动部分fn的参数对(ωn,βn)分布如图3所示。

此时振动部分回波信号参数对(ωn,βn)的分布在ωn轴方向范围相对平动部分差异性较大,可以通过设置ωn的阈值ωx有效实现振动部分的分离。

考虑到Chirplet变换运算量较大,如果对每个距离单元回波都进行分解的话,会耗费较多的时间,因此在分解回波信号之前,可以首先判定哪些距离单元内存在微多普勒信号,然后仅针对存在微多普勒信号的距离单元的有效子孔径进行Chirplet变换,这样可以大幅降低运算量。为了较快地定位微多普勒信号所在的距离单元范围,首先对目标回波进行方位向补零ISAR成像,尽管补零ISAR成像质量较低,但仍然可以通过计算ISAR成像结果中每个距离单元信号的熵来判断哪些距离单元内存在微多普勒信号。由于振动散射点在方位向上的聚焦性较差,导致其所在的距离单元信号的熵值要小于仅包含平动散射点的距离单元信号的熵值[11],因此可以判断出振动散射点所在的距离单元范围,从而有效减小运算量。该距离单元信号熵的计算公式如下:

其中:

确定微多普勒信号所在距离单元之后,采取对每一有效子孔径进行Chirplet分解而非整体补零后的孔径进行Chirplet分解的方式,针对每一子孔径长度Lh(h=1,2,…,H)确定其所需要的Chirplet原子数nh=[Lh/10](h=1,2,…,H),则某一特定的距离单元需要分解为N个Chirplet原子,其中: 3.2 稀疏孔径ISAR成像

CS理论与传统Nyquist采样定理不同,它关注的是全局信息,只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将变换得到的高维信号投影到一个低维空间,然后通过求解一个最优化问题就可以从这些少量的投影中以高概率重构出原信号,可以证明这样的投影包含了重构信号的足够信息[12]。在剔除微多普勒信号后,由式(3)可以看出目标方位向信号在频域满足稀疏性,因此可以采用CS理论来实现平动的稀疏成像。根据第2节构建的模型,假设第h( h=1,2,…,H)段子孔径前共缺失了X次脉冲回波,根据孔径的稀疏结构构造对应的观测矩阵Φ,令

采用IDFT矩阵作为稀疏变换矩阵Ψ。为高概率重构原信号,传感矩阵ΦΨ必须满足约束等距性(Restricted Isometry Property,RIP)条件[13-14],文献[12]从理论上证明了基于随机采样并利用部分傅里叶矩阵重构稀疏信号的可行性,进而通过正交匹配追踪法(OMP)[14]。来求解

Θ=min‖ΨHΦHS′c(f,τh)‖1,s.t.S′c(fg,τh)=ΦX=ΦΨΘ的最优化数学模型以完成重构,其中目标函数Θ即为所期望的方位向成像结果。当对所有距离单元都分别重构出方位向成像结果后,即最终得到目标总体散射点的二维ISAR像。

3.3 成像步骤

具体成像方法步骤总结如下:

(1)对接收到的回波信号进行补零ISAR成像;

(2)计算各距离单元信号熵,通过对比各距离单元信号熵值,设置阈值,选择熵较大的距离单元进行后续处理;

(3)对选择的每个距离单元信号内的每个有效子孔径分别进行Chirplet变换,假设某个距离单元每一Lh(h=1,2,…,H)长有效子孔径可以分解为nh=[Lh/10](h=1,2,…,H)个原子,提取对应信号分解成的N个Chirplet原子集的参数σn、tn、wn,βn的集合;

(4)通过对不同距离单元有效子孔径Chirplet原子参数wn模的最大值wnmax进行对比分析,确定对应距离距离单元中存在的振动散射点为低频振动或高频振动;

(5)针对存在低频振动散射点的距离单元,通过设置βn的阈值βx,并将βn≥βx的Chirplet原子剔除,从而有效地实现回波信号低频振动部分的剔除;

(6)针对存在高频振动散射点的距离单元,ωn的阈值ωx和βn的阈值βx,并先将ωn≥ωx的Chirplet原子剔除,进而将βn≥βx的Chirplet原子剔除,从而有效地实现回波信号高频振动部分的剔除;

(7)利用剩余的M个Chirplet原子重构对应距离单元回波信号的有效子孔,从而有效地将微多普勒干扰剔除;

(8)根据孔径的稀疏结构构造对应的稀疏观测矩阵Φ;

(9)采用IDFT矩阵作为稀疏变换矩阵Ψ,进而通过正交匹配追踪法(OMP)对所有距离单元都分别重构出方位向成像结果后,最终得到目标总体散射点的二维ISAR像。

4 实验仿真

为了验证所提方法的有效性,我们采用点散射模型进行仿真。仿真中,采用雷达的参数如下:发射信号载频fc=10 GHz,PRF=1 500 Hz,带宽300 MHz,距离分辨率0.5 m,目标本地坐标系原点O在雷达坐标系中的坐标为(30 000,0) m,平动速度为300 m/s。为模拟现实条件下飞行器颤振表现为从主体向机翼两侧呈逐渐发散趋势的特性,散射点参数如表1所示。

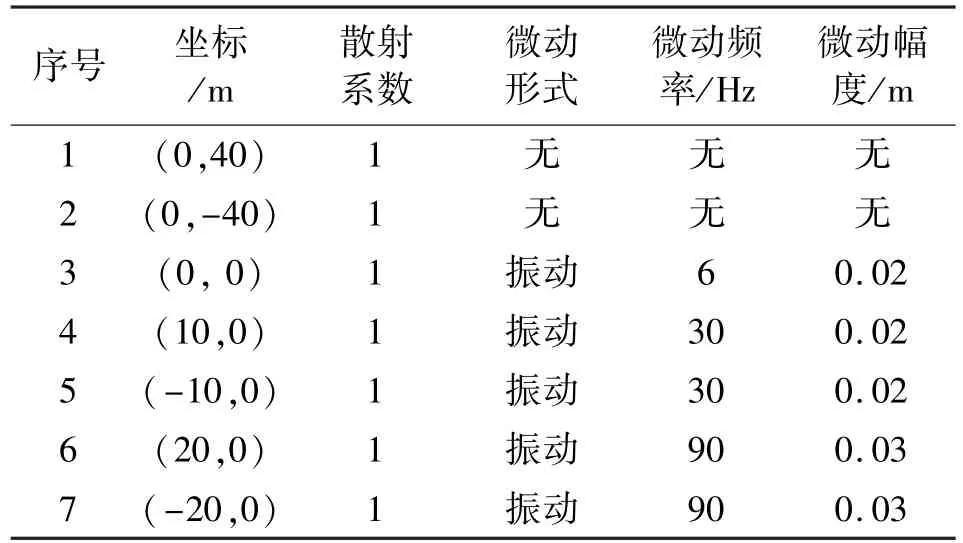
表1 散射点坐标及运动状态Table 1 The coordinates and the motion states of the scattering points

图4为稀疏度为50%的稀疏孔径条件下采用补零方式获得的目标ISAR成像结果,可见成像效果较差,真实像元之外出现了等间隔的干扰像元,且像元之间存在扰动污染。

图4 稀疏度为50%条件下成像Fig.4 Imaging with sparsity of 50%

图5 为剔除微多普勒信号之前直接采用CS方法恢复所得成像结果,虽然整体较为清晰,但是由微动所造成的干扰像元也同样被清晰的恢复出来,也就是说散焦现象仍对成像造成了影响,可见直接采用压缩感知的办法并不可行。

图5 压缩感知恢复成像Fig.5 Recovery imaging through CS

图6 为剔除微多普勒信号后采用补零处理后得到的目标ISAR成像结果,可以看出相比图4成像质量有一定改善,但是孔径的缺失对成像所造成的影响并没有的消除。

图6 剔除微动干扰后成像Fig.6 Imaging after getting rid of micro-Doppler

图7 为剔除微多普勒信号后进一步采用压缩感知恢复得到的目标ISAR成像结果,可以看出成像结果较为理想,干扰像元被有效去除,并有效消除孔径缺失所造成的污染。为了验证所提方法的鲁棒性,图8为在稀疏度为50%的稀疏孔径且信噪比为-3 dB条件下采用本文所提方法恢复得到的目标ISAR成像结果,可以看出成像结果仍较为理想,可见该方法有较好的鲁棒性。

图7 目标恢复成像Fig.7 The restored image

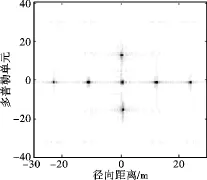
图8 -3 dB噪声下恢复成像Fig.8 Imaging when SNR=-3 dB

5 结 论

本文针对稀疏孔径下的含振动部件目标的ISAR成像问题,首先使用Chirplet变换对子孔径信号进行分解,提取了对应的Chirplet原子集的参数集,通过分析颤振散射点和平动散射点回波信号的Chirplet原子的参数的差异性,进而有效地剔除了微多普勒信号;进一步对回波信号进行方位向CS重构,最终得到了目标总体散射点的二维ISAR像。应该指出的是,本文所提方法计算量较大,在下一步的研究中,我们将继续研究具有更高运算效率的算法。

[1] 邢孟道.基于实测数据的雷达成像方法研究[D].西安:西安电子科技大学,2002. XING Meng-dao.A study of radar imaging based on the real-measured date[D].Xi′an:Xidian University, 2002.(in Chinese)

[2] 李军,邢孟道,张磊,等.一种高分辨的稀疏孔径ISAR成像方法[J].西安电子科技大学学报(自然科学版),2010,37(3):441-446. LI Jun,XING Meng-dao,ZHANG Lei,et al.High resolution imaging method for the sparse aperture of ISAR [J].Journal of Xidian University,2010,37(3):441-446.(in Chinese)

[3] 张群,罗迎,何劲.雷达目标微多普勒效应研究概述[J].空军工程大学(自然科学版),2011,12(2):22-26. ZHANG Qun,LUO Ying,HE Jin.Review of researches on micro-Doppler effect of radar targets[J].Journal of Air Force Engineering University(Natural Science Edition),2011,12(2):22-26.(in Chinese)

[4] Li H J,Farhat N,Shen Y.A New Itertive Algorithm for extrapolation of data available in multiple restricted regions with application to radar imaging[J].IEEE Transactions on Antennas Propagation,1987,35(5):581-588.

[5] 刘伟,张函信.细长机翼摇滚的数值模拟及物理特性分析[J].力学学报,2005,37(4):385-392.LIU Wei,ZHANG Han-xin.Numerical simulation and Physical C and rotating targets[J].Proceedings of the Eighth International Symposium on Signal Processing and Its Applications,2005,639-642.(in Chinese)

[6] 全炜倬,方明霞.超音速飞行器翼—身组合体的颤振研究[J].噪声与振动控制,2010,6(1):1-4. QUAN Wei-zhuo,FANG Ming-xia.Flutter Study of Wing-Fuselage Combination of Supersonic Aircrafts[J].Noise and Vibration Control,2010,6(1):1-4.(in Chinese)

[7] Chen V C,Li F.Analysis of micro-Doppler signatures [J].IEE Proceedings:Radar Sonar Navigation,2003, 150(4):271-276.

[8] 尉宇,孙德宝,岑翼刚.高斯线调频小波变换及参数优化[J].电子与信息学报,2005,27(9):1398-1403. WEI Yu,SUN De-bao,CEN Yi-gang.Gaussian Chirplet Transform and the Optimization of its Parameters.[J] Journal of Electronics&Information,2005,27(9):1398 -1403.(in Chinese)

[9] Li J,Ling H.Application of adaptive chirplet representation for ISAR feature extraction from targets with rotating parts[J].IEE Proceedings:Radar Sonar Navigation, 2003,150(4):284-291.

[10] Bell M R,Grubbs R A.JEM Modeling and Measurement for Rador Target Identification[J].IEEE Transactions on AES,1993,29(2):219-228.

[11] 保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社,2005. BAO Zheng,XING Meng-dao,WANG Tong.Radar Imaging Technology[M].Beijing:Publishing House of Electronic Industry,2005.(in Chinese)

[12] Donoho D L.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306.

[13] Candés E.The restricted isometry property and its implications for Compressed Sensing[J].Comptes Rendus Mathematic,2006,246(9):589-592.

[14] Candes E,Romberg J,Tao T.Robust Uncertainty Principles:Exact Signal Reconstruction from Highly Incomplete Frequency Information[J].IEEE Transactions on Information Theory,2006,52(2):489-509.

XU Yi-meng was born in Yancheng,Jiangsu Province,in 1989.He received the B.S.degree from National University of Defense Technology in 2011.He is now a graduate student.His research concerns radar imaging and target recognition.

Email:xuxi_aoman@163.com

管 桦(1962—),男,湖北孝感人,2003年于西北工业大学获硕士学位,现为空军工程大学信息与导航学院教授,主要研究方向为信号与信息处理;

GUAN Hua was born in Xiaogan,Hubei Province,in 1962.He received the M.S.degree from Northwestern Polytechnical University in 2003.He is now a professor.His research concerns signal and information processing.

王国正(1960—),男,陕西咸阳人,1991年于西北大学获硕士学位,现为空军工程大学理学院教授,主要研究方向为计算数学;

WANG Guo-zheng was born in Xianyang,Shaanxi Province,in 1960.He received the M.S.degree from Northwest U-niversity in 1991.He is now a professor.His research concerns computational mathematics.

张 群(1964—),男,陕西合阳人,2001年于西安电子科技大学获博士学位,现为空军工程大学信息与导航学院教授、博士生导师,主要研究方向为雷达信号处理与电子对抗;

ZHANG Qun was born in Heyang,Shaanxi Province,in 1964.He received the Ph.D.degree from Xidian University in 2001.He is now a professor and also the Ph.D.supervisor.His research interests include radar signal processing and electronic countermeasures.

周 丽(1977—),女,江苏盐城人,2002年于空军勤务学院获工学学士学位,现为工程师,主要研究方向为气象装备保障。

ZHOU Li was born in Yancheng,Jiangsu Province,in 1977.She received the B.S.degree from Air Force Institute of Service in 2002.She is now an engineer.Her research concerns providing support for meteorological equipment.

Sparse Imaging of Fluttering Target Based on Chirplet Transform and Compressed Sensing

XU Yi-meng1,GUAN Hua1,WANG Guo-zheng2,ZHANG Qun1,ZHOU Li3
(1.Institute of Information and Navigation,Air Force Engineering University,Xi′an 710077,China; (2.Institute of Science,Air Force Engineering University,Xi′an 710051,China;3.Unit 94514 of PLA,Jinan 250002,China)

In the process of Inverse Synthetic Aperture Radar(ISAR)imaging,the superposition of the phenomenon of sparse azimuth aperture caused by the uncooperative target maneuvering and the micro-Doppler effect caused by extensive fluttering in the target leads to further interference on imaging.To solve this problem,the sparse ISAR imaging model of a fluttering target is established,then the influence of sparse of aperture and fluttering on imaging is analyzed.A sparse aperture ISAR imaging method for fluttering target is proposed,which is based on Chirplet transform and Compressed Sensing(CS)reconstruction.The high quality imaging results of the fluttering target can be obtained by using the method.Simulations show the effectiveness of the proposed method.

ISAR;flutter target;micro-Doppler;sparse aperture;chirplet transform;compressed sensing

date:2013-04-07;Revised date:2013-09-02

国家自然科学基金资助项目(61172169);国家自然科学基金青年基金资助项目(61201369,61102109)

Foundation:The National Natural Science Foundation of China(No.61172169);The Young Scientists Fund of the National Natural Science Foundation of China(No.61201369,61102109)

**通讯作者:xuxi_aoman@163.com Corresponding author:xuxi_aoman@163.com

TN957

A

1001-893X(2013)10-1305-07

徐艺萌(1989—),男,江苏盐城人,2011年于国防科学技术大学获工学学士学位,现为空军工程大学信息与导航学院硕士研究生,主要研究方向为雷达成像与目标识别;

10.3969/j.issn.1001-893x.2013.10.010

2013-04-07;

2013-09-02