基于MDBZP的C/A码信号高灵敏捕获算法*

王晓君,尚 燕,孙寿浩,邱 峻

(1.河北科技大学信息科学与工程学院,石家庄050018;2.石家庄市经纬度科技有限公司,石家庄050000)

基于MDBZP的C/A码信号高灵敏捕获算法*

王晓君1,**,尚 燕1,孙寿浩1,邱 峻2

(1.河北科技大学信息科学与工程学院,石家庄050018;2.石家庄市经纬度科技有限公司,石家庄050000)

卫星信号的捕获是GPS接收机信号处理的首要任务。针对在微弱信号的情况下传统捕获方法不能很好地捕获到卫星信号的问题,提出一种改进的二倍分组块补零(MDBZP)方法为高灵敏度GPS接收机提供理论依据。该方法将连续相干积分分解成普通循环相关和随后的傅里叶变换来产生不同的多普勒频移搜索,并针对连续积分跨越多个导航电文数据位的情况给出解决方案,同时考虑了多普勒效应对码长造成的影响。仿真结果表明,此方法对低至15dB-Hz的微弱信号C/A码信号仍有较好的捕获能力。最后给出了不同载噪比情况下所对应的检测信噪比。

GPS接收机;微弱信号处理;粗捕获码;高灵敏捕获;修改的二倍分组块补零

1 引 言

全球导航卫星系统(Global Navigation Satellite System,GNSS)已经渗透到各个领域,具有广泛的应用前景。目前,要想完成对目标的定位,接收到的可见卫星必须多达4颗[1]。然而处于特殊情况下,例如森林和室内等环境,可见卫星数量比较少,接收机一般接收到不超过3颗卫星信号。究其原因,处在空旷的环境下,GPS信号较强,载噪比(C/N0)可以达到44 dB-Hz以上;处在恶劣条件下,GPS信号衰减比较严重,C/N0往往低于36 dB-Hz,必须提高接收机的灵敏度。

弱GPS信号的处理和应用正在成为一个新兴的研究热点,弱信号处理关键技术之一是信号捕获[2]。D.M,Lin.讨论了采用GPS软件接收机捕获微弱信号的问题,采用了20 ms的相干积分时间,接着又采用非相干积分,该算法利用199个非相干积分能够捕获到载噪比为21 dB-Hz的信号。D.M. Akos.对捕获弱信号的相干积分性能分析结果说明,捕获一个32 dB-Hz的载噪比信号至少需要8 ms的相干积分时间,捕获一个22 dB-Hz的载噪比信号至少需要200 ms的相干积分时间,捕获一个17 dB-Hz的载噪比信号至少需要400 ms的相干积分时间。

面对微弱GPS信号捕获的困难,本文提出了采用较少的步骤来处理长的数据相关运算,即二倍分组块补零算法(Double Block Zero Padding,DBZP),同时对该算法进行了修改,针对长时间的相关积分会跨越数据位和码长的多普勒效应问题给出了具体解决方案,从而为后面的信号跟踪部分提供了准确的多普勒频移和C/A码相位。

2 传统的基于FFT的GPS信号的捕获基本原理

传统的FFT码相位捕获算法是输入信号经过傅里叶变换后与经过傅里叶变换(FFT)的本地伪码相乘,输出结果经过傅里叶逆变换(IFFT)转换为时域信号,傅里叶逆变换输出的模值表示输入信号与本地伪码的相关结果,从而完成捕获GPS信号的算法[2]。

GPS接收机RF前端信号经过下变频的数字中频信号模型

其中,r(tk)是tk采样时刻中频信号的输出,采样间隔Ts=1/fs,d为导航数据;c为接收到的PRN码,其码长为1 023 chip,码片速率为1.023 MHz;fIF为中频载波频率,fd为多普勒频移,τ为码相位,θ0为初始相位,n为零均值、单位方差的高斯白噪声;A为信号幅度,它从噪声方差σ2n归一化为1中推导出, C/N0为载噪比(单位dB-Hz),有

假设^τ、^fd分别为码相位和多普勒的频移估计值,输入的信号和本地的载波相乘累加后得到的同相分量I、正交分量Q分别为

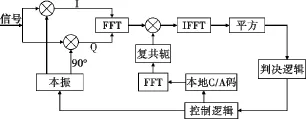
图1 FFT捕获结构框图Fig.1 FFT acquisition block diagram

3 改进的DBZP微弱C/A码信号的捕获算法

上面介绍的捕获算法通常在一个C/A码的周期里面进行运算就可以捕获到信号,但在信号微弱环境中却很难实现,想要检测出微弱信号就要进行长时间的相关积分来提高信噪比,这就需要采用微弱信号的捕获算法。

3.1 算法原理及实现步骤

修改的二倍分组块补零(Modify Double Block Zero Padding,MDBZP)方法是将连续相干积分分解成普通循环相关和随后的傅里叶变换来产生不同多普勒频移的搜索,同时考虑了码长多普勒效应所引起的问题。图2是基于MDBZP的捕获算法框图。接收信号变换成基带信号并产生

通过采样时间Ts=1/fs来设置码时延之间的间隔,在一个C/A码周期内获得Nt个码时延采样点。相干积分时间为TI,用频率间隔fres=1/TI来产生多普勒仓,每个TI时间内的数据划分成分组的块数等于多普勒仓数Nfd=2fdcovTI,其中fdcov为最大的多普勒覆盖范围。每个分组块包含S=fSTI/Nfd个采样点。

图2 基于MDBZP的捕获算法框图Fig.2 Block diagram of the MDBZP-based acquisition algorithm

第一步:将所接收的一个相干积分时间TI内的基带信号采样划分成若干个分组子块,每两个相邻的分组子块组合成一个分组块,并产生Nfd个重叠分组块,每个重叠分组块的数据长度为2S,最后一个分组子块与下一个相干积分时间的第一个数据子块合成。

第二步:考虑了多普勒补偿的本地C/A码也用相同的fS采样产生,并且划分成Nfd个分组子块,每个分组子块用S个零进行填充,每个分组块的大小为2S。为了更好的对C/A码进行多普勒补偿,在整个多普勒频移范围内等间隔设置补偿频率来生成C/A码。第i种补偿频率fdi为

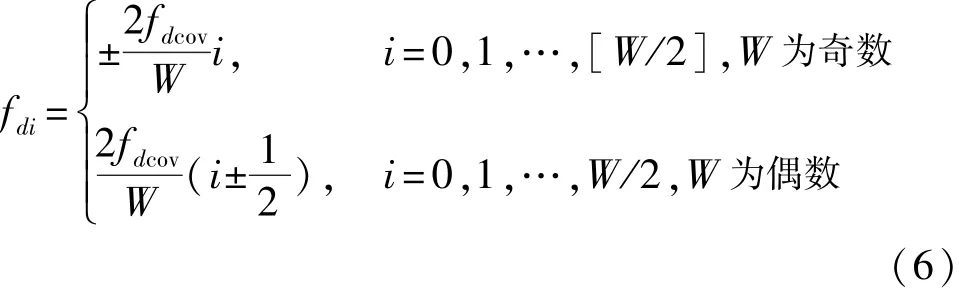
其中,W为补偿的多普勒频率种类。

第三步:将一个相干周期内所有的基带信号数据与某一种特定移位情况C/A码完成部分相关运算,称之为一个捕获步。在每个捕获步上,在接收基带信号的采样和本地产生C/A码采样的每两个对应的分组块之间进行循环相关计算,保留每个合并的分组块的最先S个循环相关值。为了叙述清楚,用二维数据索引标示每个分组块的相关结果。以第一捕获步为例,分别用(1,1),(2,1),…,(Nfd,1)标示分组块的相关结果。每个捕获步从所有的分组块中保留的点将组成大小为Nfd×S的数据矩阵。

第四步:每个捕获步将产生S个不确定的码时延的部分相干积分,对于一个C/A码所有的码时延,计算相关运算的总捕获步数为Nep,其中Nep为一个C/A码周期内计算相关运算的捕获步数,其值为Nt/S。每个捕获步中,参与相关运算的C/A码分组子块分别向左循环移动一次,每一次移动,第一个分组块就会变成最后一个分组块。在Nep个捕获步结束时,将产生一个大小为Nfd×Nt的数据矩阵,这个矩阵是Nep个Nfd×S的数据矩阵的行扩展。

第五步:对矩阵的每列做Nfd点的FFT运算得到相干积分,每个单元对应于多普勒仓和码时延的相关运算,得到矩阵Ci,i为多普勒补偿频率的序号。在矩阵Ci中对应于第i个多普勒范围的Ni行的相干积分才添加到总相干积分C中,Ci矩阵的其余行将被舍弃。

第六步:在进行L次总非相干积分后,如果矩阵中的某个单元有一个值超过门限γ,那么就可以推断出已捕获到一颗卫星,包含最大能量值的单元将对应于所估计的码时延和多普勒频移;若没有单元幅值超过设定的门限值,则未捕获该卫星信号。

3.2 多普勒效应的补偿

实现对弱信号进行捕获,需要进行长时间相干积分和非相干积分提高信噪比,多普勒效应将会对接收信号的码片长度产生影响,会导致与本地的复制码码延迟的不同,这会造成积分增益损失[4]。为了避免该情况,将整个多普勒范围划分成M个小范围来处理由码长多普勒效应引起的问题,定义fdi为第i个范围的中间频率,如公式(6)所示,以及定义Ni为在i个范围内的若干个多普勒仓数,并产生W个复制码类型,第i个多普勒范围的相干积分计算将采用第i个码类型,补偿的复制码可表示为

3.3 处理未知位边沿位置

信号捕获的过程中,相对于相干积分,非相干积分的取模运算使结果存在平方损耗,增加相干积分时间可以使平方损失减小[5]。但加长相干积分运算会出现跨越数据位的问题,为解决该情况,避免使相关运算结果跨越导航电文,就要从数据开始跳变的边沿开始对数据进行处理。由于一个数据位是20 ms,将存在20个不确定位边沿的位置,每个位边沿将对应1 ms码周期的起始点,如果相干积分的起始点没有与数据位的起始点对准,会在积分过程中存在一些损失。将采用Nb个并行的非相干积分数组来保存数据,Nb的选择不要超过20,并在20个不确定边沿范围内,均匀地选择其间隔。因此,可以算出Nb的选择总数不应该小于4。虽然4≤Nb≤20将引起一些积分损失,但是这可以减少总的处理时间,积分损失也不会影响最后的捕获结果。

3.4 处理未知数据位

当相干积分跨越导航数据位时,数据位的跳变将会影响捕获能力以及捕获的准确性[6]。算法利用一个长的相干积分时间TI,其相干积分时间为一个数据位长度Tdms的N倍,需要对N个数据位的最可靠组合进行估计,因此将有2N-1个矩阵对应于某个不确定的数据位组合,从中选择最可靠数据位的组合加到先前的总非相干积分中。由于运算量将随着N的增加呈级数增长,所以N的选择不要过大。

3.5 信号捕获性能分析

在信号捕获过程中虚警概率和检测概率是两个重要的指标,通常依据虚警概率要求确定捕获的门限,然后再根据检测概率来分析信号的捕获性能[7]。当信号捕获门限为γ时,对应虚警概率为

检测概率为

其中,β=(C/N0)MT,T=0.001 s,IL-1(x)为一阶修正贝塞尔函数,M为预检测积分时间TI的码周期数,L为整个捕获过程中的非相干积分总数。

4 仿真分析

通过对真实卫星发射的信号进行仿真,然后再把噪声叠加到模拟的数据上来产生接收机收到的信号,根据不同的信噪比来产生不同的信号幅值[8]。首先对接收机射频前端接收的信号进行下变频得到中频载波数字信号,然后把C/A码和导航电文信息加到下变频的中频信号上,在设定噪声为零均值、单位方差的高斯白噪声的情况下,根据载噪比计算公式推出信号的幅度A。本文在算法仿真时,数字中频信号的载波频率fIF=1 405 kHz,采样频率fS= 5 700 kHz,一个C/A码周期的采样点数为Nt= 5 700,相干积分时间TI=80 ms。将多普勒频移搜索范围为10 kHz,即fdcov=5 kHz。由此可知,分组块数,即多普勒仓数Nfd=800个,多普勒频率分辨力fres=6.25 Hz,每个分组块包含点数S=570个。多普勒补偿频率种类数W取为5,对应于补偿频率为(-4 kHz-2 kHz 0 Hz 2 kHz 4 kHz),非相干积分次数L=30。在积分矩阵模块中最大值元素出现位置所对应的列坐标就是基带信号的码相位,对应的行坐标标定了多普勒频率的大小。

4.1 信号的捕获结果

采用相干积分时间TI=40 ms,相当于2个数据位,非连续积分时间L=30,共计60个数据位时长的捕获算法。图3显示了在不同载噪比的情况下,归一化信号幅值时,信号的捕获结果。随着噪声的增加,捕获结果就会产生影响,在载噪比为19 dB-Hz的情况下,噪声峰值就比较大,虚警概率比较大,信号不能被捕获。

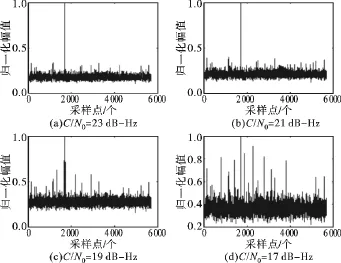
图3 2个数据位长信号的捕获结果仿真Fig.3 Two data bits signal capture simulation

采用相干积分时间TI=80 ms,相当于4个数据位,非连续积分时间L=30,共计120个数据位时长的捕获算法。图4显示了在不同载噪比的情况下,归一化信号幅值时,信号的捕获结果。在增加连续积分时间的情况下,最大相关峰值明显大于噪声峰值,信号可以被捕获。仿真结果显示,该算法可以捕获载噪比低至15 dB-Hz的微弱信号。

图4 4个数据位长信号的捕获结果仿真Fig.4 Four data bits signal capture simulation

4.2 信号的检测信噪比

在MDBZP捕获算法中,捕获门限的设定是非常重要的,通常是根据虚警概率和检测概率来得到的[9]。通过运算在矩阵模块中有最大值元素出现,那么根据其位置就可以确定码相位和多普勒频移的值,将所有单元中的最大值当作信号,在最大值周围的值也看作是处于一个码片内,其余所有的相关值看作噪声。接收机前端的采样频率是5 700 kHz, 1 ms内大约是5个采样点,所以在最大值左右各4个采样点是一个码片内的相关值,剩余单元的所有值都当成噪声来看待。信号功率和噪声功率是信号检测过程中的两个重要参数Pds和Pdn分别为

式中,M表示相关值中的最大值,b表示噪声的平均值, ni表示噪声的相关值,K表示噪声相关值的个数。

检测信噪比定义[10]为

从检测信噪比中就可以分析出不同C/N0下信号的捕获效果,如图5所示。

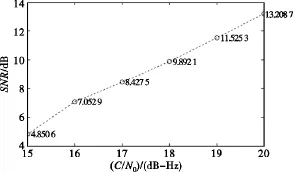
图5 信号的检测信噪比Fig.5 Detection signal-to-noise ratio of the signal

上述的仿真结果表明,采用新的处理捕获算法可以更好地捕获处于低信噪比GPS信号,很大程度上提高了检测信噪比。很明显,新的捕获方法在捕获低信噪比卫星信号时比传统FFT捕获方法有了很大的改善。

5 结 语

本文将P(Y)码捕获技术应用于微弱GPS信号的C/A码捕获,给出了一种改进的基于二倍分组块补零原理的微弱GPS C/A码信号的捕获算法及其实现步骤。算法充分考虑了C/A的多普勒频率补偿。文中讨论了如何处理未知数据位和未知位边沿位置等问题,使信号捕获不受数据位的影响。本文给出相干积分时间TI=80 ms、非相干积累次数L= 30时的仿真情况,结果表明,本算法对多普勒频率的分辨力达到6.25 Hz,可以较好地捕获到载噪比低至15 dB-Hz的微弱信号,还可以确定数据位跳变边沿的位置,可有效实现微弱GPS C/A码的捕获问题,从而实现导航系统的高灵敏定位。

[1] Xie Gang.Principles of GPS and Receiver Design[M]. Beijing:Publishing House of Electronics Industry,2009.

[2] Ziedan N I.GNSS Receivers for Weak Signals[M].New York:Artech House,2006.

[3] Morton Y T,Miller M,Tsui J,et al.GPS civil signal self -interference mitigation during weak signal acquisition [J].IEEE Transactions on Signal Processing,2007,55 (12):5859-5863.

[4] Shanmugam S K,Nielsen J,Lachapelle G.Enhanced differential detection scheme for weak GPS signal acquisition[C]//Proceedings of 2007 ION GNSS.Fort Worth:ION,2007:1-14.

[5] 胡从玮,李晓玲,安雷.一种改进的GPS微弱信号捕获方法[J].武汉大学学报,2008,33(8):821-823. HU Cong-wei,LI Xiao-ling,AN Lei.An improved methodfor GPS weak signal acquisition[J].Journal of Wuhan University,2008,33(8):821-823.(in Chinese)

[6] Wei Yu,Bo Zheng,Watson R,et al.Differential combing for acquiring weak GPS signals[J].Signal Processing,2007(87):824-840.

[7] 翟传润,张婧.GPS软件接收机微弱信号捕获算法研究[J].电子测量技术,2008,31(5):137-140. ZHAI Chuan-run,ZHANG Jing.GPS receiver weak signal acquisition algorithm[J].Electronic Measurement Technology,2008,31(5):137-140.(in Chinese)

[8] Tsui J B Y.Fundamentals of Global Positioning System Receivers a Software Approach[M].Hoboken,New Jersey:John Wiley&Sons,Inc,2005:230-235.

[9] Mark P.GNSS Solutions:Carrier-to-Noise algorithms [J].Inside GNSS,2010,5(1):20-27.

[10] Kokkonen M,Pietial S.A New Bit Synchronization Method for a GPS Receiver[C]//Proceedings of 2002 IEEE Positioning,Location,and Navigation Symposium.Palm Springs,CA:IEEE,2002:85-90.

WANG Xiao-jun was born in Chicheng, Hebei Province,in 1973.He received the Ph.D. degree from Beijing Institute of Technology in 2007.He is now a professor of Hebei University of Science and Technology and postdoctor of the 54th Research Institute of CETC.His research concerns base band signal processing in satellite navigation.

Email:eicont@139.com

尚 燕(1982—),女,河北邢台人,硕士,河北科技大学信息学院讲师,主要研究方向为信号处理、图像的稀疏表示;

SHANG Yan was born in Xingtai,Hebei Province,in 1982.She is now a lecturer with the M.S.degree.Her research concerns digital image processing.

Email:shangyan_sy@126.com

孙寿浩(1988—),男,山东德州人,河北科技大学信息学院硕士研究生,目前主要研究方向高灵敏度GNSS接收机信号处理;

SUN Shou-hao was born in Dezhou,Shandong Province,in 1988.He is now a graduate student.His research concerns signal processing in high-sensitivity GNSS receiver.

Emain:sunshouhao2010@126.com

邱 峻(1972—),男,石家庄市经纬度科技有限公司总工程师,主要从事“北斗”一代、二代系列应用终端产品研发。

QIU Jun was born in 1972.He is now a chief engineer of Shijiazhang LBH Technology Co.,Ltd..He is engaged in product development of Beidou-1 and Beidou-2 application terminals.

Email:qiujun0088@163.com

High-Sensitivity Capture Algorithm of C/A Code Signal Based on Modify Double Block Zero Padding

WANG Xiao-jun1,SHANG Yan1,SUN Shou-hao1,QIU Jun2
(1.College of Information and Science,Hebei University of Science and Technology,Shijiazhuang 050018,China; 2.Shijiazhuang LBH Technology Co.,Ltd.,Shijiazhuang 050000,China)

Signal capture is the first task of signal processing in GPS receiver.Sometimes,GPS signals are too weak to be

or processed by traditional FFT methods.A method of Modify Double Block Zero Padding (MDBZP)is presented to solve the problem of weak signal acquisition for high-sensitivity GPS receivers.At the same time,the solution with respect to continuous integration time crossing multiple data bits of navigation message is also provided and the influence of Doppler effect on code length is taken into account.The simulation results show that the method is better to capture weak GPS C/A-code signal whose carrier noise ratio is even low to 15 dB-Hz.Finally,the detection SNRs are given corresponding to different CNRs.

GPS receiver;weak signal processing;C/A code;high-sensitivity capture;MDBZP

Foundation of Hebei University of Science and Technology(No.XL201064)

TN967.1

A

1001-893X(2013)10-1299-06

王晓君(1973—),男,河北赤城人,2007年于北京理工大学获微电子学与固体电子学专业博士学位,现为河北科技大学教授、中国电子科技集团公司第五十四所博士后,主要研究方向为卫星导航基带信号处理技术;

10.3969/j.issn.1001-893x.2013.10.009

2013-04-19;

2013-06-24 Received date:2013-04-19;Revised date:2013-06-24

河北科技大学校立基金项目(XL201064)

**通讯作者:eicont@139.com Corresponding author:eicont@139.com