创业者信贷约束视阈下收入不平等与经济发展关系研究

范兆斌，袁 轶

（1.暨南大学 国际商学院，广东 珠海519070；2.哥伦比亚大学 文理学院，美国 纽约2807）

一、引 言

有关收入不平等对经济发展影响的研究框架及理论观点先后经历了古典范式、新古典范式和现代范式三个重要阶段。由于这三种范式的实证研究结果存在较大分歧，因此，进入21世纪后，随着“统一增长理论”的兴起，人们力图将古典观点、新古典观点和现代观点融合于一个分析框架（Galor和Moav，2004；Grossmann，2008；Galor，2011）。这些研究表明收入不平等对经济发展的影响依赖于经济发展阶段，两者呈非线性关系。现有文献大多以熟练劳动力与经济增长的关系为基础，鲜有文献以企业家在经济发展中的作用及其形成为基础，分析收入分配对经济发展的影响。由于创业活动经常涉及投资“门槛”问题，在信贷市场不完全的条件下，收入分配可能会通过影响企业家的形成及创业活动对经济发展产生影响。实际上，Banerjee和Newman（1993）较早就关注过该问题，他们认为在信贷市场不完全的条件下，收入不平等会通过信贷约束降低经济中的创业活动水平，从而对经济发展产生负面影响。不过该模型无法同时解释现有实证文献中所发现的收入不平等与经济发展的正向关系。本文将结合Banerjee和Newman（1993）及Galor（2011）的模型，在信贷市场不完全的条件下，以创业活动与经济发展的关系为基础，运用统一增长理论建立数理模型，综合古典、新古典和现代范式的不同观点，进一步分析收入不平等对经济发展的影响，从而解释实证文献中所发现的收入不平等与经济发展的非线性关系。

二、基本模型

设想一个经济生产并消费一种同质产品，即该产品既是资本品也是消费品。时间是无限且离散的，每期都有一群连续且规模被标准化为1的人口出生，每个人的上一代和下一代都具有单一特征，个人的偏好和能力都生来相同。每个劳动力的寿命只有两期，一生共有1个单位的劳动。

（一）效用函数。假定每个个体都具有部分“利他主义”特征，个体第一期的消费看作是父母消费的一部分，第一期的期末获得父母的代际馈赠。个人的效用由成年后（即第二期）的消费和留给下一代的馈赠共同决定。假定出生于t期的个体的效用函数为：

其中，Ut是第t代个体的效用水平，ct是t代个体第二期的消费，bt＋1是t代个体第二期末留给下一代的馈赠，z则是个体一生付出的劳动，z≤1。由（1）式可知，个体的效用与其消费和留给下一代的馈赠成正向关系，而与其付出的劳动成反向关系。为了求出个体效用最大化的消费和馈赠结构，对（1）式求ct的偏导并令其等于零，可得：

yt为t代个体一生的财富，个体的财富等于其第二期的消费和留给下一代的馈赠之和，即个体的预算约束方程为yt＝ct＋bt＋1。结合（2）式，效用函数可化为：

其中，δ＝γγ（1－γ）（1－γ）。由（3）式可知，均衡条件下，个体一生的效用水平取决于其财富和付出的劳动。

（二）职业选择。每个人有四种职业选择：工人、自我雇佣、企业主、闲置劳动力。如果个体选择做工人，则一出生就可以进入企业工作，并在两期付出其1个单位的劳动。工人一生的财富为上一代的馈赠、两期工资及利息收入之和：

其中，v表示工资，rl等于存款利率加1。由于当工资为1／δ（1＋rl）时，人们工作与否效用相同，vmin＝1／δ（1＋rl）为最低工资。当个体闲置劳动力时，其财富仅为上一代的馈赠及利息收入之和，即

如果个体选择自我雇佣，则需要在第一期付出一半的劳动接受成本为零的正规教育，以获得经营管理方面的知识，并在第二期投资I个单位的固定资本及其剩余的劳动开展经营活动。当bt＞I时，个体不需要借贷，直接以自有资金进行投资，其一生的财富为投资收益与利息收入之和：

其中，r为投资平均收益率加1。如果投资成功，则获得r1的收益率；如果经营失败，则获得r0的收益率，r1＞r0。假设投资成功的概率为q，则r＝qr1＋（1－q）r0，且r＞rl。当bt＜I时，个体需要借贷，然后用自有资金和借贷资金一起进行投资，其一生的财富为投资收益减去借款成本：

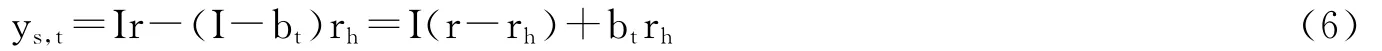
其中，rh为借款利率加1，与现实相一致，假定借款利率高于存款利率，即rh＞rl。

如果个体选择成为企业主，则跟自我雇佣一样，需要在第一期付出一半的劳动接受成本为零的正规教育，以获得经营管理知识，并在第二期开展投资活动。假定每个企业需要雇佣μ个工人，且每个工人需要配备I单位的资本，则需要投资的资金总额为μI。当bt＞μI时，直接以自有资金投资，其一生的财富为投资净收益与利息之和：

其中，r是企业主投资收益率的均值加1。如果企业主投资成功，则获得的收益率，如果投资失败，则获得的收益。假设企业主投资成功的概率为，则。为方便起见，假设企业主投资收益率的均值和自我雇佣者投资收益率的均值相等，不过和r1及和q均不相等。而当时，个体需要通过借贷创办企业，并将全部自有资金和剩余劳动投入经营活动，其一生的财富为投资净收益：

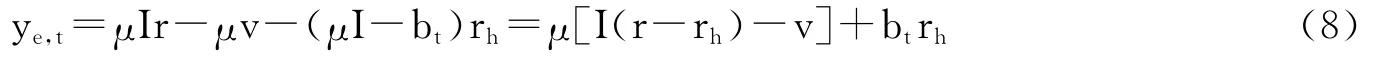
（三）信贷约束。如果工人自我雇佣或做企业主所获得的财富比原有职业高，则经济中不会有工人；而如果自我雇佣者完全通过借贷投资兴办企业，其所获得的财富比其原有职业更高，那么经济中也就不会有有企业主。相反，如果自我雇佣者所得财富低于工人，则经济中就不会有自我雇佣者；而如果企业主所得财富低于自我雇佣者或工人，则经济中也就不会有企业主。因此，为了让模型与现实相符并得到多元均衡，在此加入以下四个约束条件：

（1）如果自我雇佣者投资全部来源于借款，则净财富为负值，即I（r－rh）＜0。在最低工资水平下，如果企业主投资全部来源于借款，则净财富也为负值，即。综合可得。（2）当bt≥I时，在最低工资条件下，自我雇佣者投资所得财富不低于其做工人时的所得，即I（r－，化简得：。（3）当bt≥μI时，在最低工资条件下，企业主雇佣工人投资所得财富不低于其自我雇佣，即，化简得：＋Ir…（A3）。（4）当bt≥μI时，企业主雇佣工人投资所得财富不低于其做工人时的所得，即，化简得：

（四）代际转移对职业选择的影响。由（4）式至（8）式的财富函数和（A1）式至（A4）式的约束条件可知，个体的馈赠禀赋对其职业选择具有重要影响。结合（4）式和（5）式，可得个体在做工人和自我雇佣者之间无差异的馈赠水平

结合（6）式和（7）式，可得个体在自我雇佣和做企业主之间无差异的馈赠水平

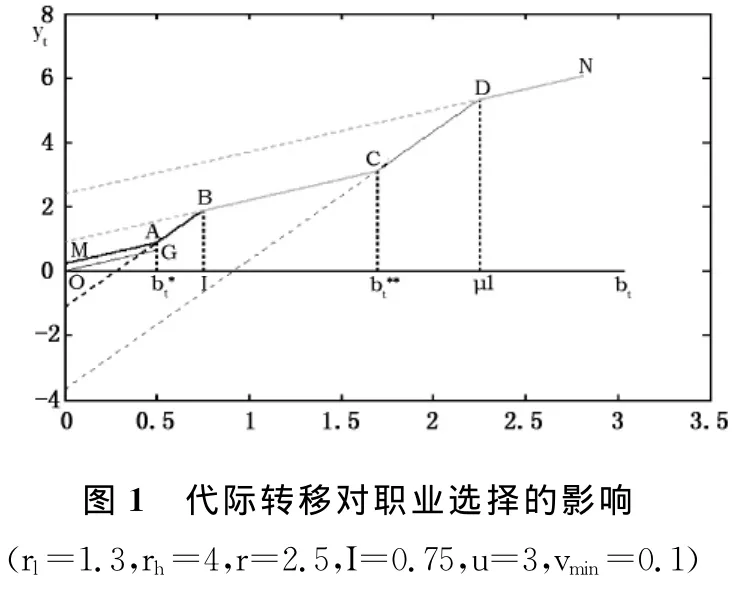
图1模拟了代际转移对个体财富及其职业选择的影响。直线MA是工人的财富－馈赠曲线，斜率为rl；直线AB是自我雇佣者中需要借贷的个体的财富－馈赠曲线，斜率为rh；直线BC是自我雇佣者中无需借贷的个体的财富－馈赠曲线，斜率为rl；直线CD是企业主中需要借贷的个体的财富－馈赠曲线，斜率为rh；直线DN是企业主中无需借贷的个体的财富－馈赠曲线，斜率为rl；直线OG则是闲置个体的财富－馈赠曲线，斜率为rl。由图1可知，馈赠禀赋低于的个体会选择做工人或闲置。馈赠禀赋位于和之间的个体会选择自我雇佣，而馈赠禀赋高于的个体会选择做企业主。

三、劳动力市场均衡

在本文模型中，工人的工资是内生的，个体职业选择及人口职业分布反过来会影响劳动力的供求及工资水平。因此，为了研究稳态，还必须研究均衡工资的决定。假定代际馈赠的分布函数为Gt（bt）。

（一）劳动力的供给函数。当工资低于最低工资vmin时，馈赠禀赋低于的个体选择做工人的效用低于闲置，从而劳动力供给为零。当工资为最低工资vmin时，工作与否效用相同，此时劳动力的潜在最大供给为。当工资高于最低工资vmin时，随着工资水平的不断上升，图1中的直线MA会逐渐向上移动，即越来越多的需要借款的自我雇佣者会选择做工人，劳动力的供给逐渐增加。当工资水平达到时，即工人与不用借贷的自我雇佣者的财富相等，图1中的直线MA平行上移直至与直线BC重合，此时原来需要借款的自我雇佣者会全部选择做工人，劳动力的最小供给量为）。由于不用借款的自我雇佣者的财富与工人相同，劳动力的潜在供给量为。当工资高于v1时，随着工资的不断上升，越来越多的需要借款的企业主会选择做工人。当工资水平达到）时，工人的财富与不需借款的企业主相同，图1中的直线MA与直线DN重合，此时原来需要借款的企业主会全部选择做工人，劳动力的最小供给量为。由于不用借款的企业主的财富与工人相同，劳动力的潜在最大供给量为经济中全部人口数量。综上所述，劳动力的供给函数为：

（二）劳动力的需求函数。当工资高于v2时，不需借款的企业主的财富低于工人，此时劳动力的需求为零。当工资等于v2时，企业主的财富与工人相同，劳动力的需求介于零和之间。当工资低于v2时，随着工资水平的下降，劳动力的需求越来越大，由决定。综合来看，劳动的需求函数为：

（三）均衡工资。劳动力市场上的均衡工资由劳动力需求和劳动力供给共同决定，这里有三种比较典型的均衡情形：

四、收入不平等的代际传递和人力资本结构的演化

由前面的静态分析可知，上一代的馈赠水平决定了下一代的职业选择及财富水平，下面以此为基础进一步分析代际转移的长期演化。结合（2）式与个体的预算约束方程，可得代际转移与财富的函数关系：

将（4）式至（8）式的财富函数分别代入（9）式，可以得到工人、自我雇佣者、企业主在各种情况下的代际转移演化函数：

闲置的劳动力只有利息收入btrl，将其代入（9）式，可得其代际转移演化函数：

为了得到长期的多元稳态，假设：

图2模拟了当经济处于最低工资vmin时，bt＋1和bt的演化关系。从中可以看出，对t代个体而言，馈赠禀赋低于m时，其后代的代际馈赠会逐渐减少，最终收敛于a，并做工人。对馈赠禀赋位于m和n之间的个体，其后代的代际馈赠会最终收敛于b，并成为自我雇佣者。而对馈赠禀赋高于n的个体，其后代的代际馈赠会最终收敛于c，并做企业主。注意到在长期中，部分借款的企业主会退化为自我雇佣者，部分自我雇佣者会退化为工人，因此无论从劳动力需求还是供给角度考虑，经济都会锁定在最低工资稳态。

图2 最低工资情形下的代际转移演化

图3 中等工资情形下的代际转移演化

图3模拟了当工资水平为v1时bt＋1和bt的演化关系。对t代个体而言，馈赠禀赋低于n时，其后代的代际馈赠会最终收敛于a，并自我雇佣或做工人。而对馈赠禀赋高于n的个体，其后代的代际馈赠会最终收敛于c，并做企业主。尽管在长期中部分借款的企业主会退化为自我雇佣者，从而减少对劳动力的需求，但由于所有个体的馈赠禀赋都达到了不用借款可以自我雇佣的水平，劳动力需求的降低会与劳动力供给的相应减少相抵消，从而对工资水平没有影响，经济将会保持在工资v1的稳态上。对高工资情形下的代际转移演化关系的分析有：对t代个体而言，无论馈赠禀赋低于n还是高于n，其后代的代际馈赠会最终收敛于n。此时，做企业家、工人或自我雇佣没有区别。经济将会在长期中保持在工资v2的稳态上。

五、收入不平等对经济发展的影响

（一）低工资稳态条件。当经济为最低工资稳态时，整个社会的总收入由四部分组成：（1）处于第一期的低收入者的工资vmin；（2）处于第二期的低收入者的工资和利息vmin＋（a＋v）（rl－1）；（3）处于第二期的自我雇佣者的投资收益和利息Ir＋（bt－I）（rl－1）；（4）处于第二期的企业主的投资收益和利息μIr－μvmin＋（bt－μI）（rl－1）。设pw、ps和pe分别为最低工资稳态时工人、自我雇佣者和企业主的人数，pw＋ps＋pe＝1。由于此时劳动力的供给大于劳动力的需求，实际参与劳动的工人数不是pw，而是μpe。整个国家的人均收入函数为：

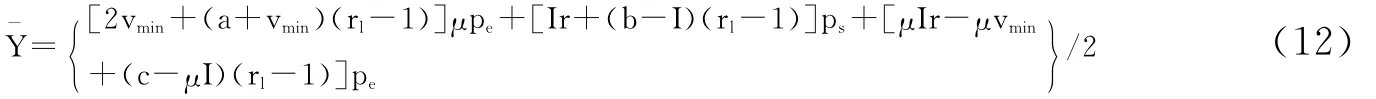
利用pw＋ps＋pe＝1，（12）式又可化为：

结合（A1）式至（A5）式可知，在低工资稳态中，工人数量的增长会使人均收入水平下降，而企业主人数的增长则会使人均收入水平上升。

我们可模拟最低工资稳态条件下初始收入分配对长期人均收入水平的影响（图略）。G1和G2是两条代际馈赠bt的分布曲线，相比G1，G2具有更高的不平等程度。由于凡是馈赠禀赋低于m的个体，其后代都将做工人，而凡是馈赠禀赋高于n的个体，其后代都将做企业主，因此在G2的情况下，长期中企业主的数量要多于G1，原因在于：较高的收入不平等程度能够使更多的个体突破信贷约束，从而选择做企业主。当然，在G2的情况下，长期中工人的数量也会多于G1，不过由于一个企业主可以雇佣多名工人，企业主数量的增加会增加工人的就业，从而从增加投资收益和增加就业两个途径提高整个社会的人均收入。这意味着当经济处于较低发展阶段时，较高的收入不平等程度有利于更多的个体免受信贷约束，开展创业活动，从而为经济突破“贫困陷阱”提供可能。该阶段的情形与古典范式关于收入不平等与经济发展关系的观点相一致。

（二）中等工资稳态条件。当经济处于中等工资v1稳态时，社会的总收入由以下四部分组成：（1）处于第一期的工人的工资v1；（2）处于第二期的工人的工资和利息v＋（a＋v1）（rl－1）；（3）处于第二期的自我雇佣者的收益和利息Ir＋（bt－I）（rl－1）；（4）处于第二期的企业主的收益和利息μIr－μv1＋（bt－μI）（rl－1）。由于工人的数量为μpe，自我雇佣者的人数为2ps－（μpe－2pw），企业主的人数为μpe，因此整个社会的人均收入为：

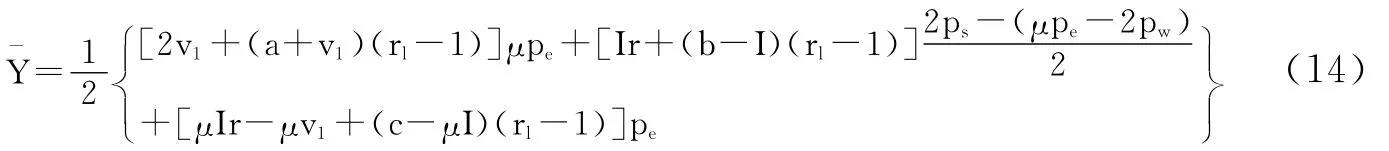
利用pw＋ps＋pe＝1，（14）式可化为：

由于在中等工资稳态条件下劳动力的需求大于供给，工人的比例对人均收入没有影响，人均收入只由企业主的数量决定。结合（A1）式至（A5）式可知，在中等工资稳态条件下企业主数量的增长仍会使社会的人均收入水平上升。

我们还可模拟中等工资v1稳态条件下收入分配对人均收入的影响（图略）。G1和G2仍是代际馈赠bt的两条分布曲线。由此可知，当整个社会进入中等发展水平时，与低收入条件下的情况恰好相反，更加平等的收入分配在长期中更有利于企业主数量的增加，从而提高整个社会的人均收入水平。原因是在中等收入水平下，较大比例人口的代际馈赠禀赋接近于企业的投资门槛μI，更加平等的收入分配有助于更多的人免受信贷约束，选择做企业主，从而在长期中增加整个社会的企业主数量，而企业主数量的增加则会提高整个社会的人均收入水平。该阶段的情形与现代范式关于收入不平等与经济发展关系的基本观点相吻合。

（三）高工资稳态条件。当经济在高工资v2条件下达到稳态时，工人、自我雇佣者和企业主三种职业的财富完全相同，因此可以直接用自我雇佣者的个体收入计算整个社会的人均收入为：。由此可知，当经济进入高工资稳态时，整个社会的人均收入与人口的职业结构无关。

我们同样可以模拟高工资稳态条件下收入分配对人均收入的影响（图略）。从中可知，当整个社会进入高收入阶段时，由于所有个体的代际馈赠长期中都会收敛于n，而且所有的职业选择都具有相同的收入，因此收入分配状况对人口的职业结构及社会的人均收入都不产生影响。该阶段的情形与新古典范式关于收入不平等与经济发展关系的观点相契合。

六、主要结论与政策含义

本文分析显示，收入不平等对经济发展的影响主要依赖于经济发展阶段。当经济发展水平较低时，收入不平等会通过降低个体创业的信贷约束，促进整个社会的创业活动，这不仅有利于社会获取投资收益，而且有利于减少失业，从而提高人均收入水平。当经济发展越过“贫困陷阱”而进入中等收入阶段时，更为平等的收入分配会使更多的人免受信贷约束，开展创业活动，从而提高整个社会的人均收入水平。当经济发展进入较高阶段时，创业活动中的信贷约束不复存在，收入不平等对人均收入也就不再具有影响。本文的模型吸收与综合了古典、新古典和现代范式关于收入不平等与经济发展关系的不同观点，解释了目前实证文献中所发现的收入不平等与经济发展的非线性关系。

自改革开放以来，我国的收入不平等程度基本呈现不断上升的趋势，基尼系数从1978年的0.21上升至1999年的0.39。进入2000年后，我国的基尼系数更是突破了4.0的“差距较大”的国际警戒线并继续攀升，目前已接近5.0的“差距悬殊”的国际警戒线（世界银行，2012）。在收入不平等程度不断提高的同时，我国的经济发展取得了举世瞩目的成就，按照世界银行的标准，2011年已经跨入了中上等收入国家行列（张其仔，2011）。这一现象正好与本文中当经济处于较低发展水平时，收入不平等与经济发展具有正向关系的预测相吻合。不过历史发展经验表明，在达到中等收入水平以后，经济通常会出现增速减缓甚至长期停滞的现象，即陷入所谓的“中等收入陷阱”。如巴西、阿根廷、墨西哥、智利和马来西亚等国家。当然也不是所有的国家都必然会陷入中等收入陷阱，日本、韩国和中国台湾地区等都成功跨越了中等收入陷阱并顺利进入了高收入经济体行列。长期陷入中等收入陷阱的国家都具有较高的收入不平等程度，基尼系数在进入中等收入阶段后都基本长期保持在5.0以上。根据本文的模型，在信贷市场不完全的条件下，这种收入分配方面的两极分化正是经济达到中等收入水平后阻碍人力资本持续积累和经济持续增长的原因。结合本文模型的分析及其他国家的发展实践，及时调整当前的收入分配政策，缩小收入差距无疑是今后我国保持经济持续增长的重要途径。第一，我国已经跨入中等收入国家行列，而且经济增长速度已经有所趋缓；第二，目前我国收入差距过大已经成为公认的事实，并且今后还有继续恶化的迹象；第三，信贷市场不完全是我国改革和发展相对比较迟缓的金融市场的重要特征，新创企业及中小企业普遍面临严重的信贷约束。不过需要注意的是，根据本文的模型分析，收入分配政策的调整应该是向中等收入群体倾斜，因为这一群体更容易通过分配政策的微调免受信贷约束，而且人口比重较大，能够产生较强的规模效应。

［1］张其仔.产业蓝皮书：中国产业竞争力报告（2012）［M］.北京：社科文献出版社，2011.

［2］Carree M A，Thurik A R.The impact of entrepreneurship on economic growth ［J］.Handbook of Entrepreneurship Research，2010，5：557－594.

［3］Galor O.Inequality，human capital formation and the process of development［R］.NBER Working Paper，No.17058，2011.

［4］Graevenitz V G，Harhoff D，Weber R.The effects of Entrepreneurship Education［J］.Journal of Economic Behavior ＆Organization，2010，（76）：90－112.

［5］Grossmann V.Risky human capital investment，income distribution，and macroeco nomic dynamics［J］Journal of Macroeconomics，2008，30（1）：19－42.

［6］Samila S.Venture capital，entrepreneurship，and economic growth［J］.Review of Economics and Statistics 2011，93（1）：338－349.