开孔率对开孔板消浪效果影响的数值模拟研究
陈雪峰,张 梅,李玉成
(1.大连大学土木工程技术研究与开发中心,大连116622;2.大连理工大学海岸及近海工程国家重点实验室,大连116023)
开孔率对开孔板消浪效果影响的数值模拟研究
陈雪峰1,张 梅1,李玉成2
(1.大连大学土木工程技术研究与开发中心,大连116622;2.大连理工大学海岸及近海工程国家重点实验室,大连116023)
采用VOF方法,结合k-ε紊流模型建立数值波浪水槽。造波边界采用内源造波法,造波边界后方和波浪水槽出口边界均采用海绵层消波,自由面采用F函数追踪,从而数值模拟了波浪对开孔板的作用。将开孔板前波浪反射系数的数值计算结果与文献[14]的物理模型实验结果进行比较,验证所建立的数值模型及计算方法的正确性。通过改变开孔率,模拟波浪与开孔板作用的开孔板前波浪的反射系数,进而分析了开孔率与波浪反射率的关系。同时,分析了波浪作用下开孔板的迎浪面与背浪面的点压力差变化,并主要探讨开孔率与点压力差的相互影响关系。分析结果表明:随着开孔率α的增大,反射率减小,透射率增大,点压差呈非线性变化。
开孔板;反射率;压力差;VOF方法
开孔结构作为减小结构物前的波浪反射及降低波浪作用力的一种新型结构,已进行了不少的研究。国内外很多学者对波浪与开孔结构之间作用力进行了研究,并对作用力与其影响因素之间的相互关系进行了分析。主要有Franco[1]等通过现场观测研究了波浪与实体结构及全开孔结构相互作用的波浪力,并与试验资料进行对比,给出了实体及开孔结构的水平力和垂直力的统计分布值。Tanimoto[2]等对开孔沉箱的反射率与主要影响因素作了范围较广地研究,并做了一定的理论分析,给出了消浪室相对宽度与沉箱前反射系数的关系。Tabet-Aoul[3]对具有不同开孔板的开孔结构的点压力及总水平力进行了试验研究,分析了相位差对波峰水平力的影响,提出了计算开孔板及后实体板的最大波浪力公式。
戴冠英[4]、张芹[5]等通过物理试验给出开孔率较小(ε<0.25)时直立全开孔板或全开孔板后带实体墙两种结构形式的波浪反射率及结构所受的波压力变化规律,并给出波浪反射率、透射率及点压力与主要影响因素之间的关系,得出反射率、透射率及点压力与相对水深的回归关系式。马宝联[6]等通过物理模型试验分析研究了无顶板开孔沉箱式防波堤的反射率和有顶板与无顶板开孔沉箱式防波堤的堤前反射率的比值与主要影响因素之间的关系,给出了反射率、相位差的计算关系式。陈雪峰,李玉成[7]等利用二维规则波水槽试验,对规则波作用下,有顶板开孔结构各个部位所受到的压力分布进行了研究,并系统地分析了各部位压力与影响因素之间的关系。Chen[8]等利用流体体积法(VOF方法)结合k-ε紊流模型,对规则波与开孔结构的相互作用进行了数值模拟,得出影响开孔结构反射率以及总水平力的主要因素,并对总水平力与影响因素之间的相互关系进行了分析。Wang[9]等应用有限差分法和VOF方法建立了一个三维数值模型来研究波浪与开孔沉箱的相互作用,得出了作用于开孔椭圆形沉箱上的波浪力随着其开孔率的增大而显著减小。Huang[10]等比较全面地总结了含有实体后墙和没有后墙的开孔或开槽防波堤的传播和反射特性,同时也总结了作用于开孔沉箱上的波浪力的几种计算方法。刘勇等[11]基于线性势流假定,对斜向波作用下带横隔板局部开孔沉箱防波堤的水平波浪力进行了理论研究并指出增加单个开孔沉箱的长度有利于减小结构所受总水平波浪力。在研究波浪与防波结构物之间作用力的数值造波过程中,很难消除反射波的二次反射对入射波的干扰。王永学[12]提出了无反射造波,为有效地处理反射波的局部波动提供了基础。韩朋[13]在波浪出流边界设置了海绵层消波,采用了5种不同的消波系数对波浪进行消波分析,为海绵层的消波提供了理论依据。LI[14]等通过物理模型试验给出了不同开孔形状和开孔率的开孔板的透射系数和开孔板前波浪的反射系数的变化规律。CHEN[15]等通过数值计算和物理模型试验相结合的方法分析研究了规则波作用下有顶板开孔沉箱的受力问题。
上述文献对反射率、作用力与其影响因素之间相互关系的研究中,关于开孔率对反射率、波浪力的影响关系的研究鲜见报道。本文主要是基于VOF方法结合k-ε紊流模型建立的波浪数值水槽,对波浪作用下开孔板所受点压力及反射率进行数值分析,并分析影响反射率、点压力分布的影响因素,尤其是开孔率的影响。
1 数学模型、控制方程、边界条件及数值计算方法
1.1 数学模型
波浪与开孔板相互作用的控制方程可简化为二维雷诺时均Navier-Stokes方程,采用F函数追踪波浪自由面,即改进的VOF方法。本文的造波采用的是内源造波外配海绵层消波的方法,该方法可以有效地解决数值波浪水槽中的二次反射问题。图1是二维数值波浪水槽中部分波浪与开孔板相互作用的示意图,图中坐标系的选择及各变量定义如下:以造波板与水槽底面的交点作为坐标原点,x轴正向沿波浪前进方向,y轴正向竖直向上。d为开孔板前的静止水深,c为入射边界海绵层消波厚度,cl为开孔板厚度,b为开孔板宽度,a为开孔板的开孔尺寸,e为两相邻开孔中心间距。
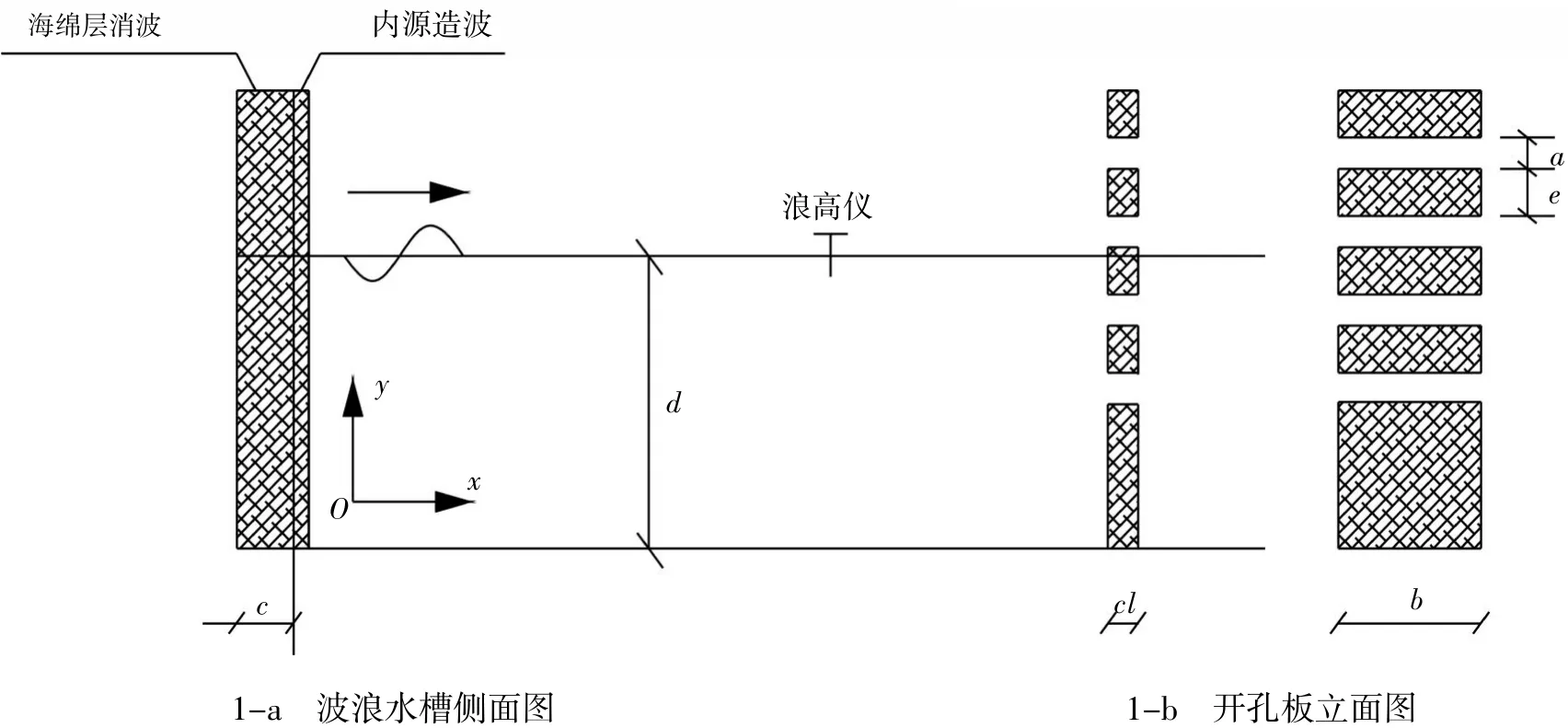
图1 波浪对开孔板作用示意图Fig.1 Sketch of a wave acting on perforated plate
1.2 控制方程
假设流体为不可压缩的黏性流动,其控制方程为
连续方程

动量方程
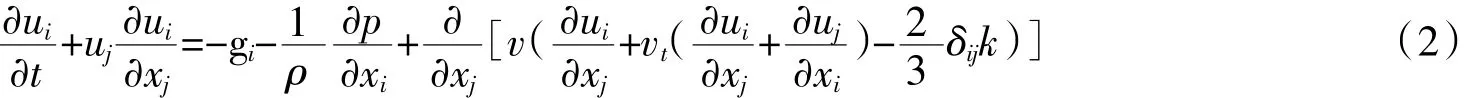
k-ε方程
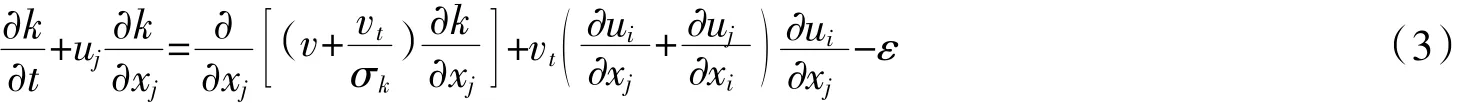
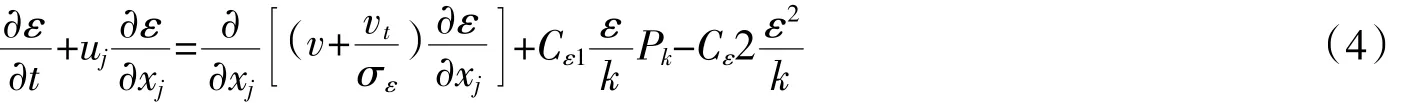
1.3 边界条件
1.3.1 造波边界
采用内源造波外配海绵层消波的边界,造波区域Ω内其方程为

式中:S为Ω区域内的一个质量源函数,定义为S=βsinωt arctan(t/T),β为造波系数,ω为波频,T为周期。
为了防止造波板的左边界产生二次反射,在造波板的后侧边界设置了一定长度的海绵层来吸收反射波,海绵层的阻尼衰减系数[13]表达式如下
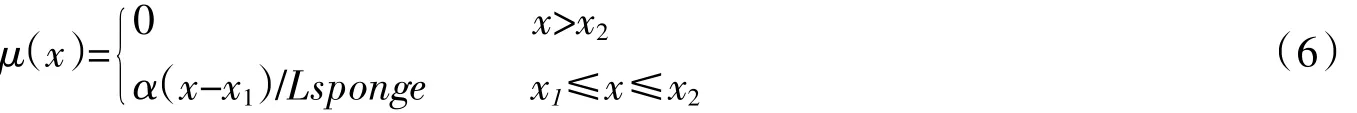
应用该衰减系数在动量方程式(2)的右端增加一个阻尼项。
1.3.2 自由表面
为了描述波浪运动的自由面,引入流体体积函数的概念。流体体积函数F的定义为单元内流体所占有的体积与该单元可容纳流体体积之比。由定义可知:若单元体内充满流体时,F的值为1.0;当单元体为空单元时,F的值为0;表面单元体的F值介于0和1之间。这些单元或者与自由表面相交,或者含有比单元体积小的气泡。自由表面单元的定义为含有非零的F值,且与他相邻的单元中至少有一个是F值为零的空单元。F函数应该满足如下的方程

F函数是阶梯函数,不能采用平常一般的差分方式,因此在VOF方法计算中,采用施主与受主单元模型来计算F函数的变化以保持其不连续的特性。
1.4 数值计算方法
VOF方法在求解微分方程组时采用有限差分法,计算域剖分成矩形非均匀网格,y方向网格大小以孔口尺寸为参考值均匀划分,x方向在开孔板前1/4倍波长范围内以1 cm等间距划分,非均匀网格区域以相邻网格的1.01倍逐渐变疏,达到波长的1/60倍间距时又等间距划分。应该注意的是,由于计算中没有考虑越浪现象,y方向的网格数代表的总高度要大于水深加波高之和与结构物纵向尺寸的最大值。
2 物理模型试验
规则波与开孔板的物理模型试验[14]是在大连理工大学海岸和近海工程国家重点实验室的波流水槽内进行的。水槽尺寸为长69 m,宽2.0 m,深1.8 m,试验水深d采用0.35 m。开孔板采用1.0 cm厚的有机玻璃制成,总尺寸为宽0.80 m,高0.70 m,置放在平底埋基床上。孔型为矩形横条开孔,实验中的开孔率α取0.2和0.4两组,当开孔率为0.2时,孔高为3.8 cm,孔宽为14.2 cm;当开孔率为0.4时,孔高为7.6 cm,孔宽为14.2 cm。
试验中所采用的规则入射波周期分别为1.0 s、1. 20 s、1.40 s,相应的波长分别为1.13m、1.50 m、2.00 m,波高分别为0.06m、0.08m、0.10m。表1给出了试验的波浪条件及无量纲参数的变化规律。

表1 模型参数和实验条件Tab.1 Model parameters and experiment conditions
3 数值计算结果和试验结果的对比
为了验证本文所建立的数学模型,计算方法以及所编写程序的正确性,将开孔率为0.2时,开孔板前波浪的反射率的数值计算结果与试验结果[14]进行对比,将试验值和计算值绘于图2中,横坐标是实测反射率,纵坐标是数值计算的反射率。将开孔率为0.2时,开孔板后波浪的透射率的数值计算结果与试验结果[15]进行对比,将试验值和计算值绘于图3中,横坐标是实测透射率,纵坐标是数值计算的透射率。两张图中的实线是x=y,虚线是y=x的±10%的包络线。由图可以看出,大部分点在y=x的±10%的包络线内,说明数值计算结果与物理模型试验结果吻合较好。
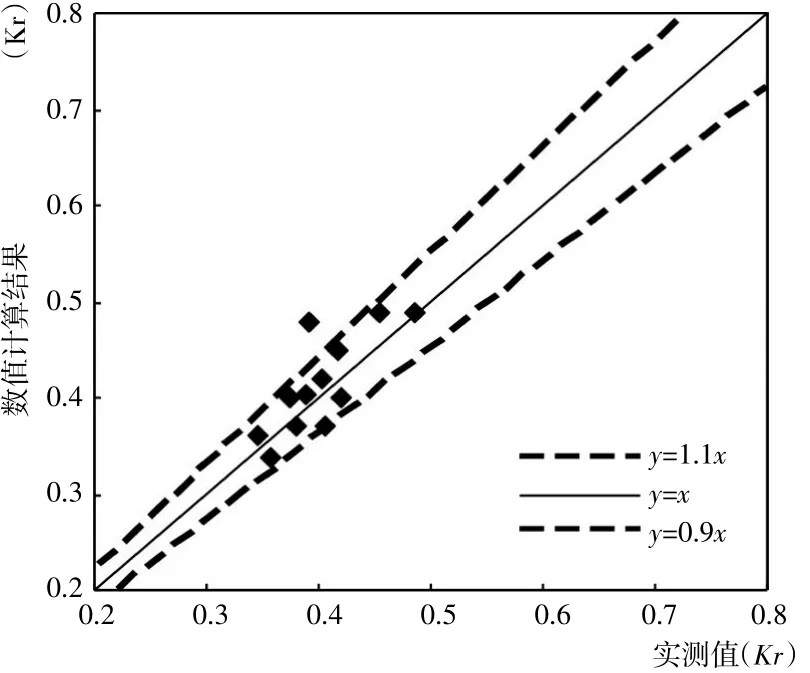
图2 反射率的数值计算结果和实测结果的比较Fig.2 Calculated vs.measured results(Kr)
4 开孔率对反射率的影响分析
波浪在传播过程中,如遇到地形突变或建筑物时会产生波浪反射,反射率(Kr)与各主要影响因素之间的相互关系式可以表示为

文献[2]、[9]分析给出:d/L与反射率之间呈线性递增的关系,H/L与反射率呈线性递减的影响关系。本文通过改变开孔率而保持其他影响因素不变的方法,着重分析开孔率对反射率的影响。
规则波作用下的数值计算过程中,各参数的选取如下:相对水深d/L为0.16~0.36,波陡H/L为0.02~0.10,水深d为0.40m,开孔板的开孔率分别取为0.10、0.15、0.20、0.25、0.30、0.35、0.40。
图4显示了只改变开孔率α而其他影响因素不变,得到开孔率α与开孔板前波浪的反射率之间的影响关系,横坐标表示开孔率,纵坐标表示反射率。该图说明当开孔率α增大时,反射率呈非线性减小趋势。
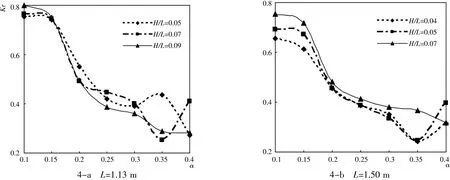
图4 α与点反射率Kr的相互关系Fig.4 Relationship ofαand Kr
5 开孔率对透射率的影响分析
波浪在传播过程中,遇到开孔板时部分波浪会透过开孔板而产生波浪透射,透射率(Kt)与各主要影响因素之间的相互关系式可以表示为

文献[4]总结出在规则波作用下,开孔板的开孔率为20%时,透射系数均随相对波高H/d、波陡H/L的增大而减小。这里保持其他影响因素不变而改变开孔率的方法来着重分析开孔率对透射率的影响。
图5显示了只改变开孔率α而其他影响因素不变,得到开孔率α与开孔板后波浪的透射率之间的影响关系,横坐标表示开孔率,纵坐标表示透射率。该图说明当开孔率α增大时,透射率呈非线性增大趋势。
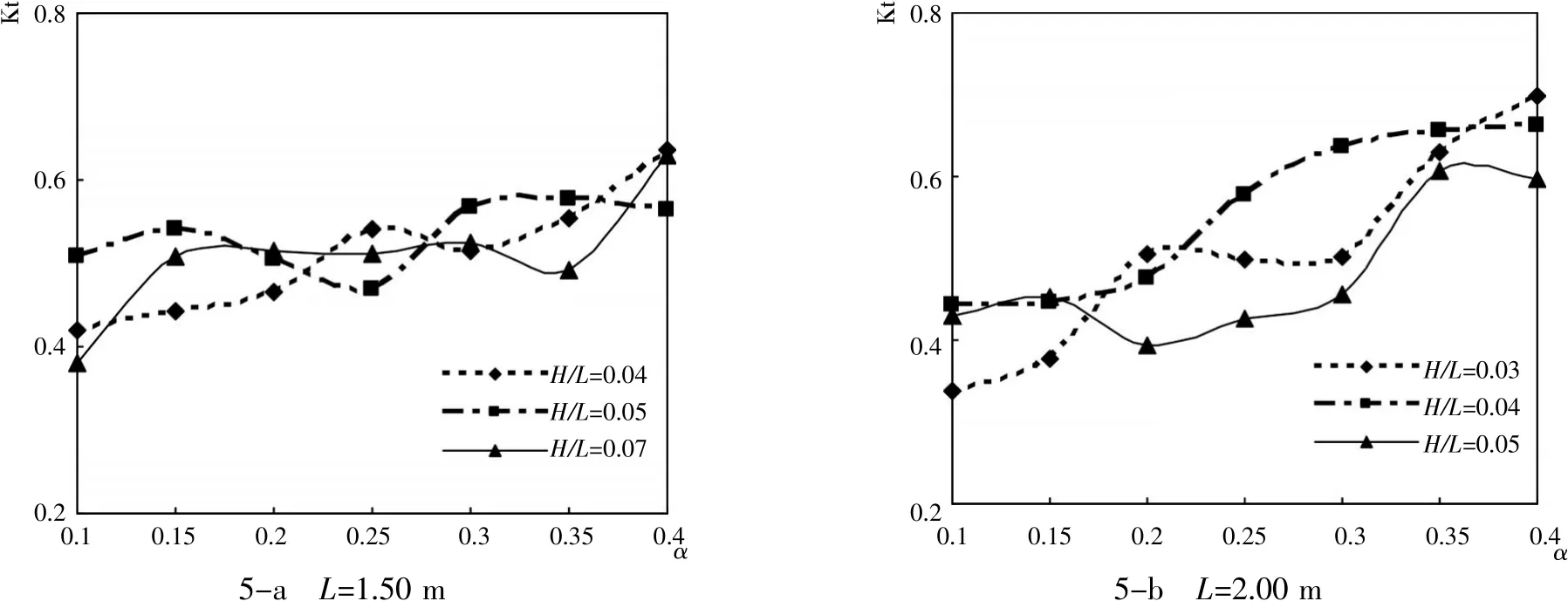
图5 α与点透射率Kt的相互关系Fig.5 Relationship ofαand Kt
6 开孔率对开孔板所受压差的影响分析
为分析开孔板对于减小波浪力的有效性,作者分析了点压力与各主要影响因素之间的相互关系。其关系式可以表示为

文献[7]、[8]、[15]等通过水槽试验和数值模拟分析研究给出:不同位置处d/L、H/L等影响因素与各处压差及压强,总水平力等呈线性相关。通过改变开孔率而保持其他影响因素不变的方法,本文着重分析开孔板迎浪面与背浪面的压差与开孔率的相互影响关系。
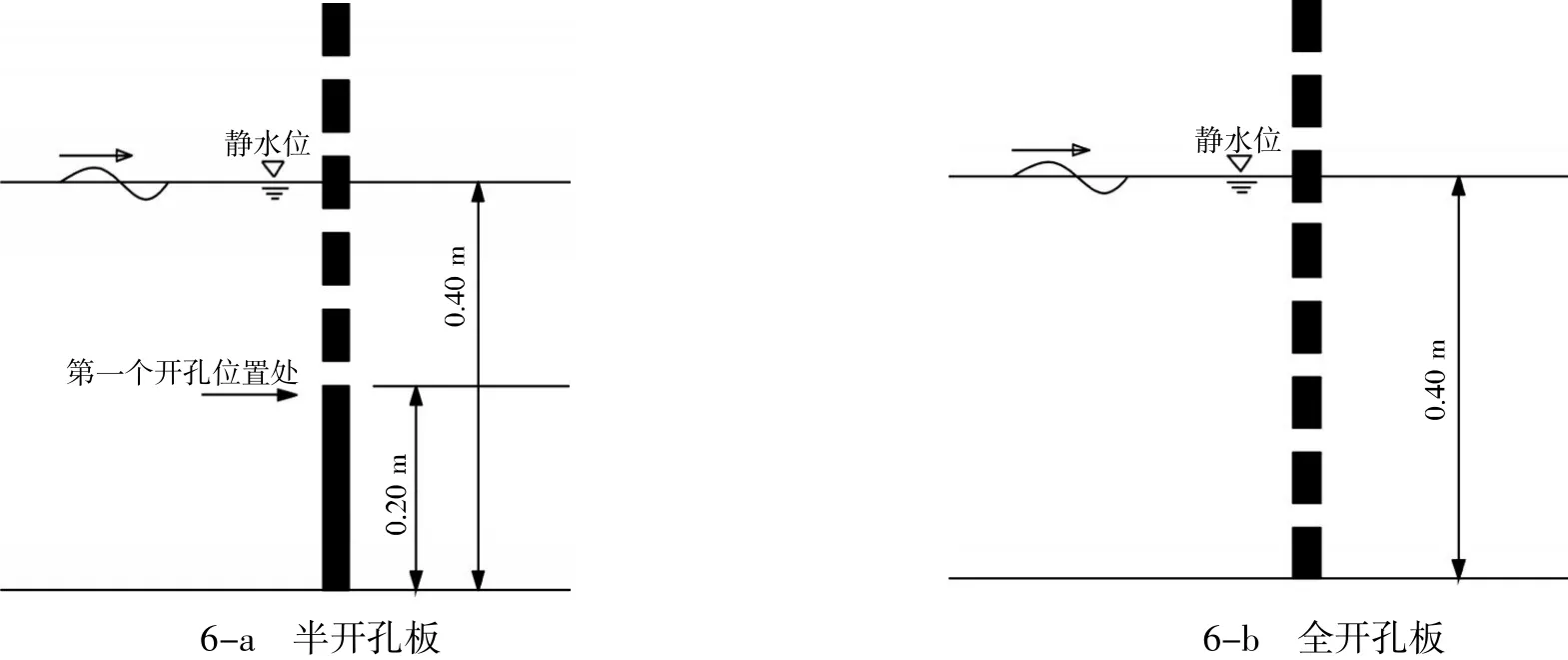
图6 开孔板示意图Fig.6 Sketch of perforated plate
定义开孔板迎浪面与背浪面的压差ΔP的正压方向与波浪传播方向一致,选取流体密度ρ,重力加速度g和波高H为基本量,对压差进行无量纲化,用ΔP/ρg H表示。以开孔板的静水位附近及静水位以下第一个开孔位置处的点(位置如图6所示)为例来分析规则波作用下,开孔板波峰作用下点压差与开孔率的影响关系。
图7显示了只改变开孔率α而其他影响因素不变,得到在波峰波浪力作用下,开孔板静水位附近的点压差与开孔率α之间的影响关系,横坐标表示开孔率,纵坐标表示波峰波浪力作用下开孔板所受的压差。图7说明当开孔率α增大时,波峰波浪力作用下开孔板上的压差呈非线性变化。
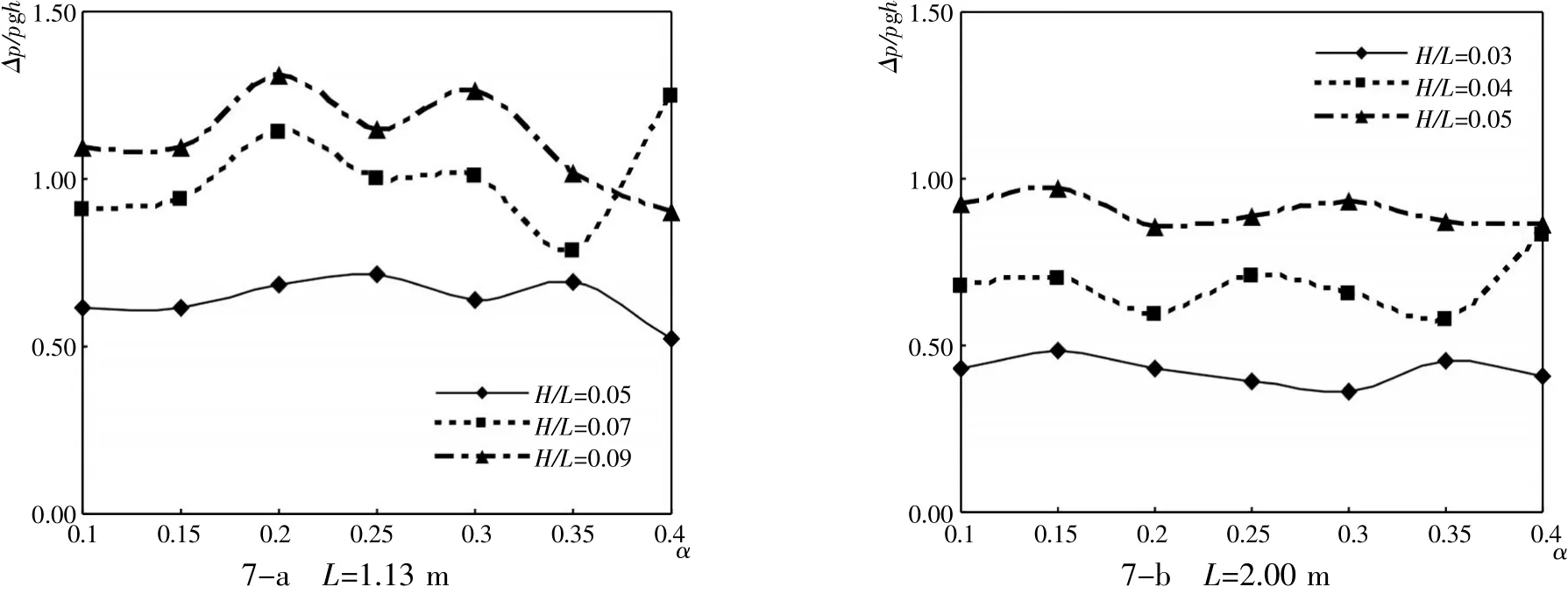
图7 α与压差Δp的相互关系(静水位处)Fig.7 Relationship ofαandΔp(in static water level)
图8显示了开孔板在静水位以下第一个开孔位置处的内外压差受开孔率影响的变化规律。由图可知,当开孔率α增大时,波峰波浪力作用下该位置处的压差呈非线性变化。

图8 α与压差Δp的相互关系(静水位以下第一个开孔位置处)Fig.8 Relationship ofα and Δp(the first perforated position below static water level)
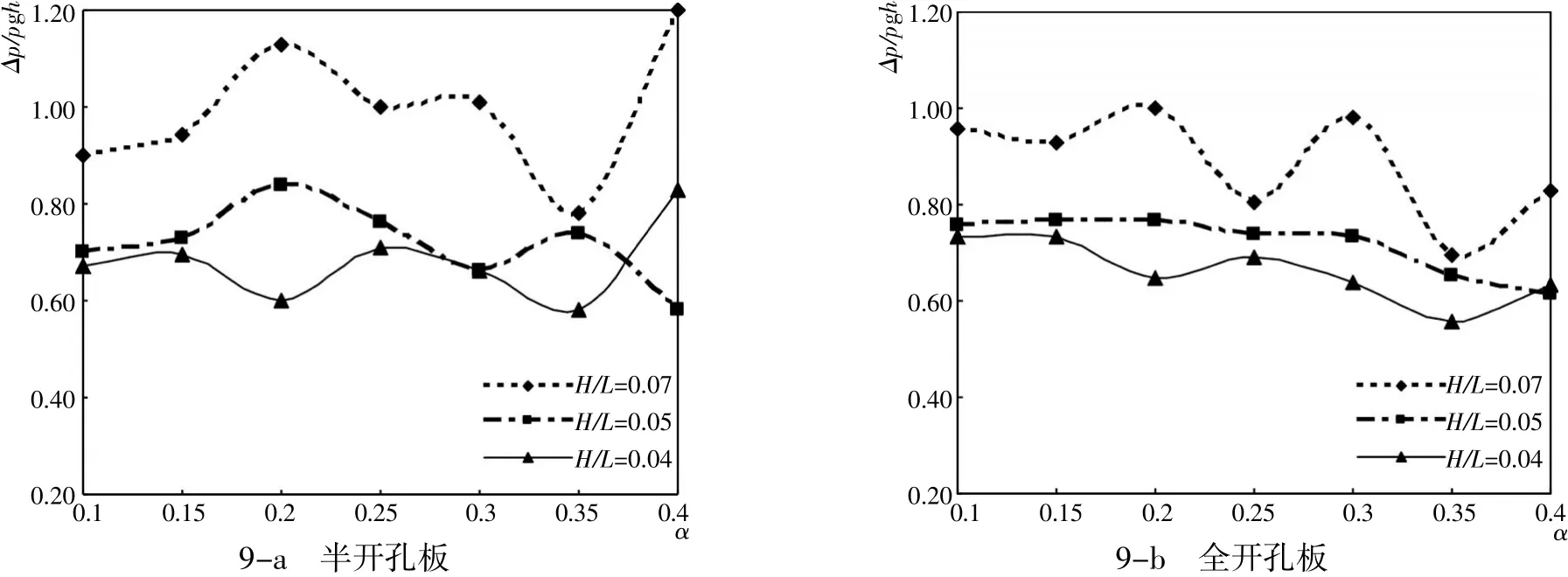
图9 半开孔板和全开孔板的压差Δp与开孔率之间关系Fig.9 Relationship of pressure difference Δp and porosity(partially perforated plate and entirely perforated plate)
为了进一步分析开孔位置对开孔板的消浪性能的影响,以波高0.08m为例,分析了静水位下一半位置至顶部开孔的开孔板(半开孔板)与全开孔板的迎浪面与背浪面的点压差的相互关系(图9)。由图可知,当开孔率α相同时,波峰波浪力作用下半开孔板与全开孔板所受的压差相比较,部分半开孔板的压差略大。这说明半开孔板和全开孔板的减压性能相比较,全开孔板在降低波浪力方面略好一些。结构稳定和设计考虑,可以选择设计适合形式的开孔板。
同时,为了比较在一定条件下半开孔板与全开孔板前的波浪反射率大小情况,以波高为0.08 m为例来分析,如图10所示。
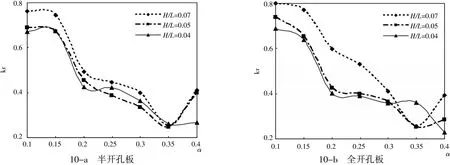
图10 半开孔板和全开孔板的反射率Kr与开孔率之间关系图Fig.10 Relationship between Kr and porosity(partially perforated plate and entirely perforated plate)
图10是在波浪条件相同的条件下,半开孔板与全开孔板前波浪的反射率受开孔率影响的情况。由图可知,当开孔率α相同时,多数情况下,半开孔板与全开孔板前波浪的反射率相差不大,变化规律基本相似。这说明半开孔板和全开孔板的消浪性能相差不大,结构稳定和设计考虑,可以选择设计适合形式的开孔板。
7 结论
通过不同开孔率下波浪与开孔板相互作用的数值模拟,分别计算出了开孔板前波浪的反射率、开孔板后波浪的透射率以及开孔板的迎浪面与背浪面的点压差。并就开孔率对它们的影响进行了主要分析,从中可以看出:开孔率对开孔板前波浪的反射率、开孔板后波浪的透射率及开孔板的迎浪面与背浪面的点压差影响规律类似。随着开孔率α的增大,反射率减小,透射率增大,点压差呈非线性变化。最后还分析了半开孔板与全开孔板的消浪性能,通过波高为0.08m的计算结果的对比,可知半开孔板和全开孔板的消浪性能相差不大,为结构稳定和设计考虑,可以选择设计需要形式的开孔板。
[1]Franco L,Gerloni M De,Passoni G,et al.Wave forces on solid and perforated caisson breakwaters:comparison of field and laboratory measurements[C]//ASCE.Proc.26th ICCE.America:ASCE,1998:1 945-1 958.
[2]Tanimoto K,Yoshimoto Y.Theoretical and experimental study of reflection coefficient for wave dissipating caisson with a permeable front wall[J].Report of the Port and Harbour Research Institute,1982,21(3):846-850.
[3]Tabet-Aoul E H,Lambert E.Tentative new formula for maximum horizontal wave pressures acting on perforated caisson[J]. Journal of Waterway,Port,Coastal and Ocean Engineering,2003,129(1):34-40.
[4]戴冠英.波浪作用下开孔直立结构的反射与透射性能[J].水利水运科学研究,1993(3):291-300. DAIG Y.Reflection and transmission performances of vertical perforated structure under wave action[J].Hydro-Science and Engineering,1993(3):291-300.
[5]张芹,戴冠英.波浪对开孔直立结构作用力的试验研究[J].水利水运科学研究,1994(4):367-374.ZHANG Q,DAIG Y.Experimental study on interaction between waves and vertical perforated structures[J].Hydro-Science and Engineering,1994(4):367-374.
[6]马宝联.波浪与开孔直墙式防波堤的相互作用[D].大连:大连理工大学,2004.
[7]陈雪峰,李玉成,刘勇,等.有顶板开孔沉箱上构件所受规则波波浪力的研究[J].中国海洋平台,2005,20(3):1-10. CHEN X F,LIY C,LIU Y,et al.Study of regular wave forces on component of perforated caissons with top cover[J].China offshore platform,2005,20(3):1-10.
[8]CHEN X F,LIY C,WANG Y X,et al.Numerical simulation of wave interaction with perforated caisson breakwaters[J].China Ocean Engineering,2003,17(1):33-43.
[9]WANG Y X,REN X Z,DONG P,et al.Three-dimensional numerical simulation ofwave interaction with perforated quasi-ellipse caisson[J].Water Science and Engineering,2011,4(1):46-60.
[10]HUANG Z H,LIY C,LIU Y.Hydraulic performance and wave loadings of perforated/slotted coastal structures:A review[J]. Ocean Engineering,2011(1):1-24.
[11]刘勇,李玉成,滕斌,等.带横隔板局部开孔沉箱在斜向波作用下的受力研究[J].海洋学报,2008,30(2):137-146. LIU Y,LIY C,TENG B,et al.Theoretical study of diagonal wave forces acting on partially perforated caisson breakwater with transverse walls[J].Acta Oceanologica Sinica,2008,30(2):137-146.
[12]王永学.无反射造波数值波浪水槽[J].水动力学研究与进展:A辑,1994,9(2):205-214. WANG Y X.NumericalWave Channelwith AbsorbingWave-maker[J].Journal of Hydrodynamics:A,1994,9(2):205-214.
[13]韩朋,任冰,李雪临,等.基于VOF方法的不规则波数值波浪水槽的阻尼消波研究[J].水道港口,2009,30(1):9-13. HAN P,REN B,LIX L,etal.Study on damping absorber for the irregular waves based on VOF method[J].Journal of Waterway and Harbor,2009,30(1):9-13.
[14]LIY C,LIU Y,TENG B.Porous effect parameter of thin permeable plates[J].Coastal Engineering,2006,48(4):309-336.
[15]CHEN X F,LIY C,TENG B.Numerical calculation and simplified methods on the wave force acting on perforated caissons with top cover[J].Coastal Engineering,2007,54:67-75.
Numerical simulation study on effect of porosity on performance of perforated structures
CHEN Xue-feng1,ZHANG M ei1,LIYu-cheng2
(1.Research and Development Center for Civil Engineering Technology,Dalian University,Dalian 116622, China;2.State Key Laboratory of Coastal and Offshore Engineering,Dalian University of Technology,Dalian 116023,China)
The VOF method and k-εmodel were utilized to establish the numerical wave flume.The internal source generation of wave was applied in wave area whose end was placed the sponge layer to absorb the reflection of wave.The free surfaces were treated by a function F.Then numerical results of reflection coefficient before perforated plate were compared with the experimental results of reference[14]to verify the numerical method.Therefore,numerical simulation can be adopted to study the interaction of wave with perforated structures.By changing porosity,the effect of porosity on reflection coefficient can be analyzed.Moreover,the pressure difference between the outer and inner of perforated plate was researched when the porosity was changed and other parameters kept constant,so that the mutual influence of porosity on the pressure difference was obtained according to the numerical results.A conclusion is drawn that increasing the porosity,the reflection coefficient is decreased,the transmission coefficient is increased and the pressure differences trend nonlinear change.
perforated plate;reflection coefficient;pressure difference;VOF method
TV 139.2;O 242.1
A
1005-8443(2013)04-0285-08
2012-11-08;
2012-12-18
大连理工大学海岸及近海工程国家重点实验室开放基金资助项目(LP1103)
陈雪峰(1973-),女,辽宁省大连人,教授,主要从事波浪与结构物相互作用研究。
Biography:CHEN Xue-feng(1973-),female,professor.

