《结构力学》一则习题“怪异”结果的分析
2013-06-28 03:10王广利
重庆三峡学院学报 2013年3期
王广利
(黎明职业大学土木建筑工程学院,福建泉州 362000)
在《结构力学》[1]中有一则习题,要求画出简支梁在均布的分布力偶作用下的剪力图和弯矩图,如图1所示.
本习题的求解并不难,利用平衡条件先求出约束反力,得FAY= - m,FB= - m(负代表与假定的指向相反),如图2所示.再用截面法截开距A端为x的任意截面,取左边为隔离体(如图3所示),并取平衡,得此截面上剪力和弯矩的表达式分别为(1)式和(2)式,此二式即为梁的剪力方程和弯矩方程(将A端视为坐标原点).
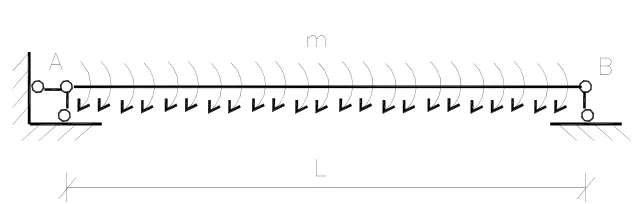
图1

图2

图3

将已有结果FAY= - m,代入(1)式,得Q(x) = - m,进一步可得M(x) = 0.于是可得梁的剪力图和弯矩图,如图4(a)和图4(b)所示.

图4


图5是直杆中截出的长度为dx的微元,这个微元上作用的荷载不仅有分布力q(x)(规定向上为正),还有分布力偶m(x)(规定顺时针为正)。

图5
由∑Fiy=0可得
Q( x)+ q( x)· dx= Q( x)+ dQ( x),从而得到

由∑MC=0可得
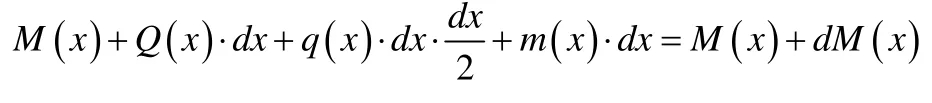


2 结论与讨论
(1)从式(4)可以看出,分布力偶对弯矩的影响类似于集中力;
3 结 语
在工程结构实际问题中,几乎不会出现分布力偶荷载作用的情况,因此,在《结构力学》教材中没有涉及分布力偶荷载,但作为教学一线的力学工作者则有必要对力学原理和方法的前提条件及适用范围有一个清晰的认识.
[1]袁驷.定性结构力学(网络课程),清华大学结构力学精品课程网站.http://www.civi l.edu.cn/smsolver/user/Qual it ySM/index.htm.
[2]孙训方,等.材料力学:第三版[M].北京:高等教育出版社,1994.
猜你喜欢
英语文摘(2021年4期)2021-07-22
现代临床医学(2019年4期)2019-09-10
建材发展导向(2019年5期)2019-09-09
中国生物医学工程学报(2019年3期)2019-07-16
智富时代(2018年2期)2018-05-02
智富时代(2018年2期)2018-05-02
中学历史教学(2017年12期)2018-01-19
材料科学与工程学报(2016年2期)2017-01-15
新课程研究(2016年3期)2016-12-01
中国教育技术装备(2015年4期)2015-03-01

