6度1-正则Cay ley图

李靖建,徐尚进,杨旭

(1.云南大学数学与统计学院,云南昆明 650031;2.广西大学数学与信息科学学院,广西南宁 530004)

6度1-正则Cay ley图

李靖建1,2,徐尚进2,杨旭2

(1.云南大学数学与统计学院,云南昆明 650031;2.广西大学数学与信息科学学院,广西南宁 530004)

试图对6度1-正则Cayley图给一个完全分类.利用无核的概念将图自同构群归结到对称群S6的子群.然后根据1-正则图的性质构造出所有可能的具有非交换点稳定子群的无核6度1-正则Cayley图,进一步证明了构造出的图都是有核的,由此给出了这一类图的一个完全分类.

1-正则;Cayley图;无核

DO I：10.3969/j.issn.1008-5513.2013.05.005

1 引言

2 预备知识

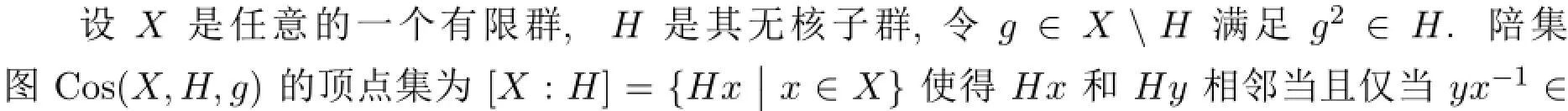
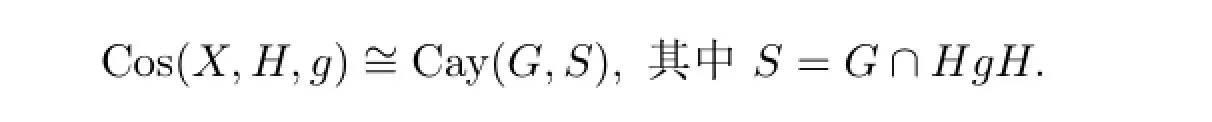
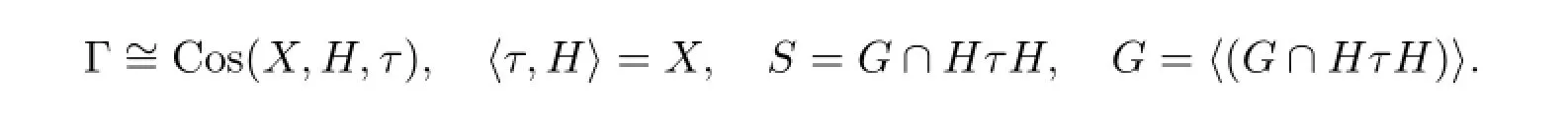
3 定理的证明

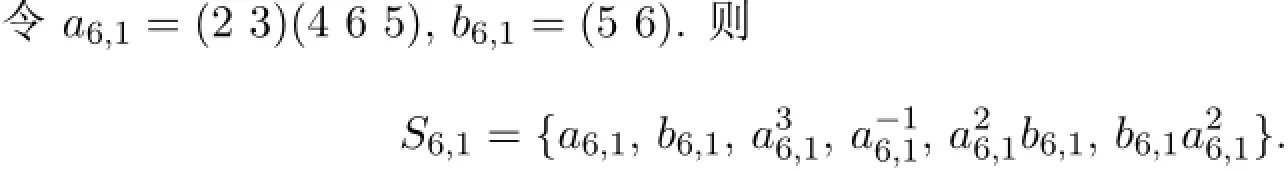
[1]Li C H.Finite s-arc transitive Cayley graphs and f ag-transitive pro jective p lanes[J].Proc.Amer.M ath. Soc.,2005,133(2):31-40.

[2]Frucht R.A one-regular graph of degree three[J].Can.J.M ath.,1952,4(1):240-247.

[3]Conder M D E,Praeger C E.Rem arks on path-transitivity in f nite graphs[J].Eu ropean J.Com bin., 1996,17(4):371-378.

[4]Li Jingjian,Lu Zaiping.Cubic s-transitive Cayley graphs[J].Discrete M ath.,2009,309(3):6014-6025.

[5]Xu Shangjin,Fang Xingui.5-arc transitive cubic Cayley graphs on f nite sim p le groups[J].European J. Combin.,2007,28(4):1023-1036.

[6]Conway JH,Curtis R T,Norton S P,et al.Atlas of Finite Groups[M].Oxford:Oxford University Press, 1985.

[7]Huppert B,B lackburn N.Finite G roups III[M].New York:Springer-Verlag,1982.

1-regu lar Cay ley graphs o f va len cy 6

Li Jingjian1,2,Xu Shangjin2,Yang Xu2

(1.School of M athem atics and Statistics,Yunnan University,Kunm ing 650031,China;
2.School of M athem atics and In form ation Sciences,Guangxi University,Nanning 530004,China)

This paper is trying to give a com p lete classif cation of 1-regu lar Cayley graphs of valency 6.By the def nition of core-free,this paper reduces the graph automorphism group to a subgroup of symmetric group S6. Furthermore,by the p roperties of 1-regu lar graph,this paper constructs all the 1-regular Cayley graphs w ith nonabelian stabilizers and p roves that every such graph is not core-free.Thus a classif cation of such graphs is given.

1-regu lar,Cay ley graph,core-free

O157

A

1008-5513(2013)05-0472-05

2013-06-22.

国家自然科学基金(10961004,11226141,11361006);广西自然科学基金(2013GXNSFAA 019018,2013GXNSFBA 019018).

李靖建(1976-),博士,讲师,研究方向：群与图.

徐尚进(1959-),博士,教授,研究方向：群与图.

2010 MSC:05C25