变压器电压差动保护方法研究
王 雪,王增平
(华北电力大学新能源电力系统国家重点实验室,河北 保定 071003)
0 引言
在变压器差动保护中,如何区分励磁涌流和内部故障电流是其固有的、不可回避的问题[1]。目前实际运行的变压器差动保护主要利用二次谐波含量来识别励磁涌流,但随着铁心工艺的改进,饱和磁通倍数下降为1.2左右,甚至更低,励磁涌流中的二次谐波含量可能低于10%,同时由于无功补偿装置和输电线路分布电容的影响,变压器内部故障时也会产生较大的二次谐波,这样就难以确定合适的二次谐波制动比,保护存在不正确动作的风险[2]。国内外文献已提出了众多的励磁涌流识别方法,其中大部分文献利用某种数学工具或算法提取涌流波形某方面的特征[3-6],具有一定的识别效果,但由于影响励磁涌流的因素很多,仅凭某一方面的外在特征均不能保证任何情况下差动保护都不会误动,部分文献提出利用模糊数学理论综合多个判据识别涌流[7-8],虽然取得了较好效果,但识别过程更加复杂,将会影响差动保护的快速性。
近些年来不受励磁涌流影响的变压器主保护受到人们的重视,进行了有益的研究,取得了一定的成果[9-12]。其中基于功率差动的主保护通过检测变压器消耗的有功功率的大小来判别变压器是否发生内部故障[9],该保护不再依赖励磁涌流的波形特征,但需要躲过励磁涌流开始的充电过程以及此时产生的较大的铁耗,将会降低保护的灵敏度。基于回路方程的变压器主保护从正常变压器回路方程出发得到主保护判据。其中一类判据为根据回路方程差值的大小来判别变压器是否发生内部故障[10-11],该判据需要考虑变压器漏电感参数计算误差的影响,另一类判据根据变压器线圈漏电感的变化情况来识别内部故障[12],利用回路方程计算三相等值漏电感,根据它们之间的差异情况判断变压器运行状态,当发生相间短路时,由于三相等值漏电感计算值都很小,该判据存在灵敏度低甚至失效的问题,必须补充其他判据。
本文在正常变压器回路方程的基础上定义了补偿电压的概念,分析了在各种不利条件下补偿电压的幅值和相位变化特征,据此提出了综合补偿电压幅值和相位特征的变压器电压差动保护。仿真分析结果验证了该保护的正确性和可行性。
1 补偿电压的定义
单相双绕组变压器如图1所示,i1、i2分别为两侧线圈电流。

图1 单相双绕组变压器Fig. 1 Single-phase two-winding transformer
根据电路原理可得单相变压器两侧回路方程为
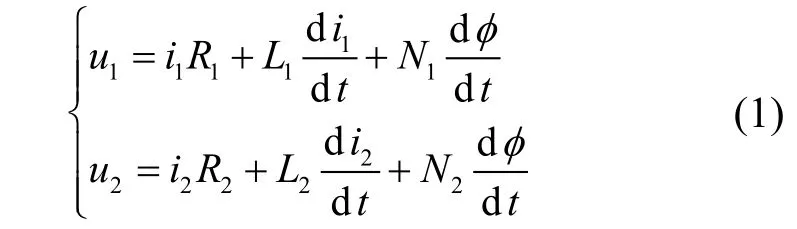
式中:u1、u2分别为两侧电压;R1、L1、R2、L2分别为两侧线圈的电阻和漏电抗;N1、N2分别为两侧线圈的匝数;φ为主磁通。
定义变压器两侧的补偿电压分别为
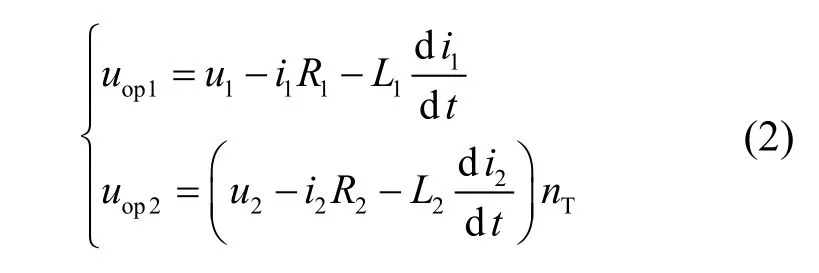
式中:nT为变压器变比,等于两侧线圈匝数比,为了分析简便,后文中假设nT=1。
Υ/Δ-11接线的三相两绕组变压器如图2所示。图中 iLa、iLb、iLc、iA、iB、iC分别为Δ侧和Υ侧各线电流,ia、ib、ic分别为Δ侧各线圈电流。
根据单相变压器的分析过程,可得三相变压器两侧的补偿电压分别为

图2 三相双绕组Υ/Δ接线变压器Fig. 2 Three-phase two-winding Υ/Δ transformer
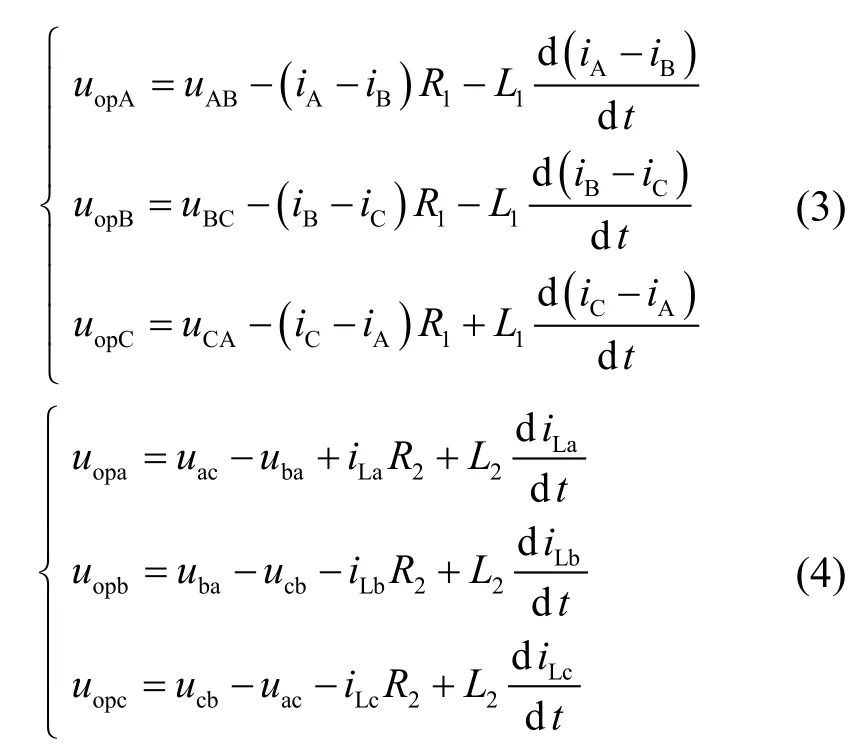
2 基于回路方程差值的保护不平衡输出分析
变压器回路方程是根据正常状态下模型得到的,外部故障、励磁涌流等运行状态下,变压器内部结构以及参数没有变化,该方程总是成立的,这样两侧的补偿电压总是相等的。当变压器内部发生故障时,回路方程不再成立,两侧补偿电压之间就会产生差值。定义回路方程差值为两侧补偿电压之差,即

可以根据回路方程差值的大小来判断变压器内部发生故障。
从前面分析可以看到基于回路方程差值的保护需要首先获得变压器两侧线圈的电阻和漏电感。利用有限元方法可以准确计算变压器线圈的漏电感[13],但是该方法需要详细的变压器铁心及线圈的结构参数,由于大多数情况下很难获得这些参数,该方法的应用受到很大限制。另一种方法是利用短路实验数据计算变压器两侧线圈总漏电感,然后假定每侧线圈的漏电感为总漏电感的一半[10,14],实际上变压器设计过程中总漏电感并不是平均分配的,比如同心式布置时高压线圈一般位于外侧,高压侧漏电感可能占总漏电感的75%~90%[15],因此简单地按照总漏电感一半来计算线圈漏电感必然存在误差,使得外部故障或励磁涌流等运行状态下保护存在不平衡输出。此外变压器调压分接开关位置改变以及CT变换误差也会影响到保护性能。本节将针对这些问题进行分析。
为了分析过程方便,给出变压器补偿电压和回路方程差值的相量形式为

变压器正常时,补偿电压相量图如图3。
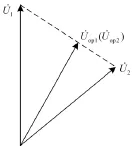
图3 正常时补偿电压相量图Fig. 3 Compensated voltage phasor under normal condition
两侧补偿电压的幅值和相位均相同,回路方程差值等于零。
2.1 调压分接开关位置改变的影响
变压器调压分接开关位置改变时变压器变比将随之变化,从式(6)可知这只会影响二次侧补偿电压的幅值,不会影响相位,此时相量图如图4。
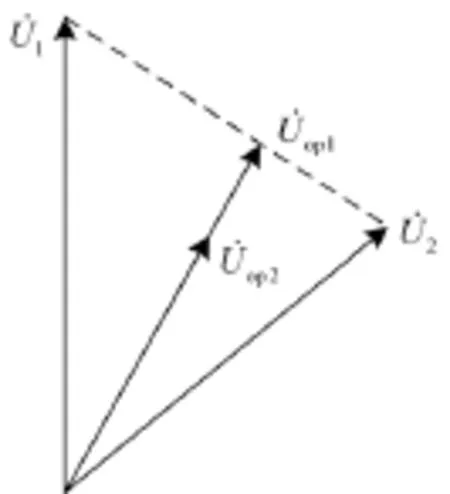
图4 分接开关位置改变时补偿电压相量图Fig. 4 Compensated voltage phasor when tap position changes
设变压器实际变比为(1+ΔU),将实际变比代入式(6)、式(7)可得此时补偿电压和回路方程差值。回路方程差值的大小与调压开关位置的关系为
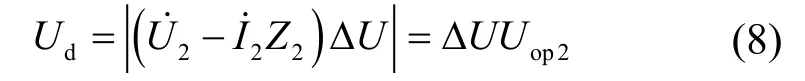
可见回路方程差值的大小将随调压幅度增大而增大。
2.2 变压器漏阻抗计算误差的影响
利用短路实验所得变压器漏阻抗的精度完全可以满足工程计算要求,这里仅考虑各侧线圈漏阻抗占总漏阻抗的计算比例和实际比例不一致对保护的影响。应用中一般假设各侧漏阻抗为总漏阻抗的一半,设该假设导致的计算误差分别为ΔZ1和ΔZ2,满足

两侧补偿电压公式为
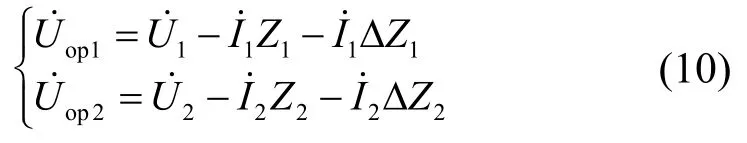
将式(9)、式(10)代入式(7),可得回路方程差值为
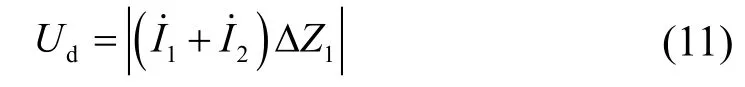
式中,两侧电流之和为变压器励磁电流。
当一次侧空载合闸时,如果忽略变压器等值电路中的电阻分量,则二次侧电压等于一次侧电压在等值励磁电抗上的分压,二者同相位。二次侧电流为零,因此二次侧补偿电压不受漏阻抗计算误差的影响,仍等于二次侧电压,但一次侧补偿电压幅值发生变化,如图5(b)所示。此时回路方程差值不再为零,但两侧补偿电压的相位仍相同,实际中考虑电阻分量后会有一个较小的相位差。
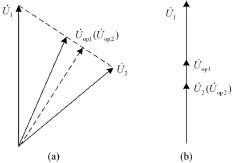
图5 考虑漏阻抗计算误差时补偿电压相量图Fig. 5 Compensated voltage phasor when the computation error of leakage impedance is considered
2.3 CT变换误差的影响
变压器励磁涌流和外部故障时的暂态电流中含有较大的非周期分量和谐波分量,很容易造成 CT饱和,产生较大的变换误差。考虑最严重的情况,这里以变压器二次侧出线发生金属性短路和励磁涌流两种状态为例分析 CT变换误差的影响。设 CT变换误差造成的电流变化量分别为此时两侧补偿电压分别为
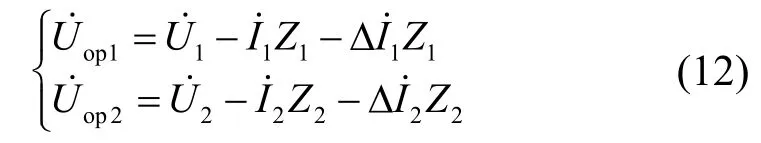
回路方程差值为
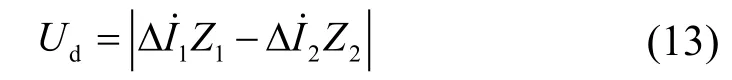
变压器外部出线发生金属性短路时,二次侧电压为零。补偿电压相量如图 6(a)所示,此时两侧的补偿电压不再相等,由于CT饱和造成电流的幅值误差程度比相位误差要大,因此补偿电压间将产生较大的幅值差,而相位差相对比较小。空载合闸产生励磁涌流时补偿电压相量图如图6(b)所示,此时两侧补偿电压间可能会出现较大的幅值差,但相位差仍较小,实际中考虑电阻分量后相位差会略有增大。
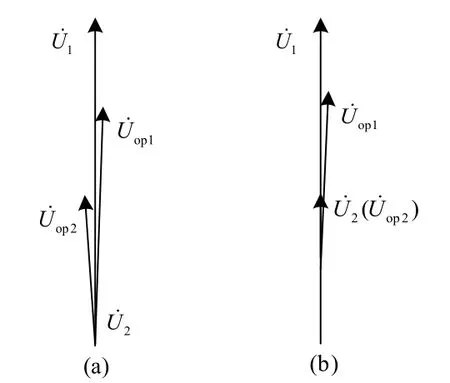
图6 考虑CT变换误差时补偿电压相量图Fig. 6 Compensated voltage phasor when the transformation error of CT is considered
3 电压差动保护判据
从前面分析可知在几种不利因素的影响下,基于回路方程差值的保护在变压器正常时会产生较大的不平衡输出,保护的动作门槛值必须大于可能出现的最大不平衡输出,显然这样会降低变压器内部故障时保护的灵敏度。考虑到补偿电压间的相位关系受到影响较小或完全不受影响,引入补偿电压间相位关系以便提高保护的灵敏度。综合两侧补偿电压间的幅值和相位特征,构成如下电压差动保护判据:
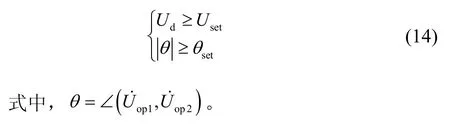
式(14)中的任一判据满足时,可以判断为变压器内部发生故障。该判据在电压平面上的动作特性如图7所示。
图7中横纵坐标分别为
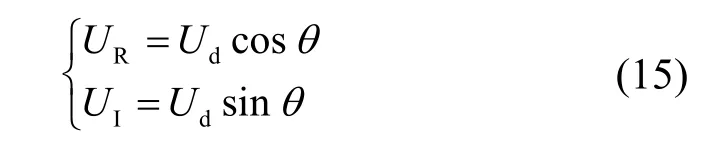
本文电压差动保护动作特性为图7中实线围成的扇形,外部为动作区,而基于回路方程差值的保护的动作特性如图7中虚线圆所示,圆外为动作区。相对于基于回路方程差值的保护,电压差动保护的动作区扩大了,有利于提高内部故障时保护的灵敏度。
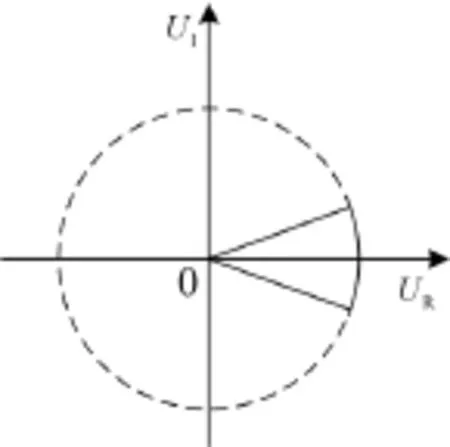
图7 电压差动保护动作特性Fig. 7 Performance characteristic of voltage differential protection
4 验证分析
4.1 ATP仿真系统
为了验证本文提出的电压差动保护的性能,利用ATP软件建立图8所示变压器仿真系统,其中正常变压器采用饱和变压器模型,内部故障变压器采用自互感模型[16]。变压器的相关参数取自一台动模实验变压器,该变压器由三单相变压器构成,采用Υ/Δ-11接线,额定容量为10 kVA,低压侧额定电压为380 V,高压侧额定电压为460 V,空载电流为1.45%,空载损耗为1%,短路损耗为0.35%,短路电压为12.0%,高压侧线圈78匝,低压侧线圈112匝。仿真之前首先根据该变压器铁心和线圈的结构数据,利用有限元分析的方法计算获得仿真模型中的电感参数[13],归算后高低压侧漏电感分别为2.3 mH和1.6 mH,利用实验的方法获得变压器励磁特性曲线。
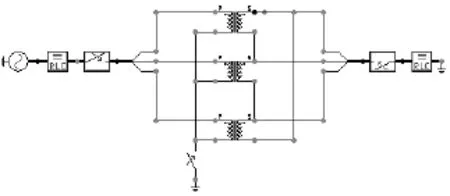
图8 变压器仿真实验系统图Fig. 8 System for transformer simulation
仿真过程中系统阻抗取0.7+j2.1 Ω,为解决Δ侧参考电位问题,用阻值为1010Ω的大电阻模拟空载状态,采样频率为5 kHz。充分考虑了可能出现的合闸时刻、剩磁以及合闸初相角的取值,使仿真结果能够全面反映变压器运行状态。在高压侧设置故障,最小故障匝数为2匝,最大为42匝。文献[13,16]分析了该仿真过程和结果的正确性,这里不再重复。
4.2 电压差动保护性能分析
表1给出了变压器本身正常时,在励磁涌流、外部故障状态下本保护可能出现的不平衡输出情况。每种状态均包含多组数据,考虑了诸如合闸时刻、剩磁、外部故障位置等因素的影响。一般变压器最大调压范围为±10%,这里变比误差取最大值10%。计算过程中假定两侧线圈漏抗相等,此时两侧漏抗参数误差分别为-19.6%和15.6%。对于 CT变换误差,本文考虑相位误差不超过10°,幅值误差不超过20%。
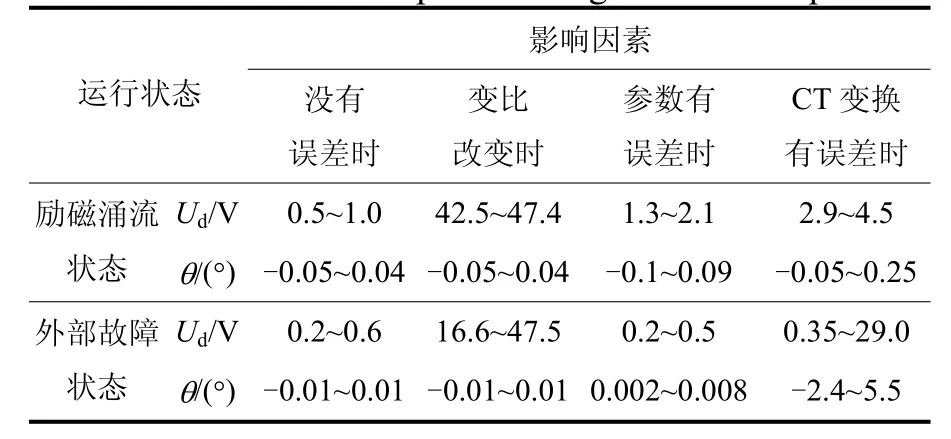
表1 电压差动保护的不平衡输出Table 1 The unbalanced output of voltage differential protection
从表1可以看到,计算过程中没有误差时,保护的不平衡输出很小,其中幅值输出不超过1.0 V,相位输出不超过0.05°,主要由计算过程中的舍入误差造成。调压抽头位置改变造成变比变化时,补偿电压相位差仍然很小,各种状态下均不超过0.05°,但幅值不平衡输出急剧增大,最大时达47.5 V。不同状态下,漏感参数误差对保护的影响不同,外部故障时没有影响,不平衡输出和没有误差时相比没有明显变化;励磁涌流状态下不平衡输出略有增大,相位不平衡输出可达 0.09°,幅值不平衡输出可达2.1 V。外部故障状态下CT变换误差对保护的影响最大,此时的相位和幅值输出最大可达5.5°和29.0 V。上述计算结果和前面的理论分析相吻合。
以往的研究中主要依靠实验数据来确定保护的定值,如文献[10]中将定值确定为 20 V。从前面的计算结果可知在一定的条件下保护的不平衡输出可能会超过该门槛值,造成保护误动。由于调压开关位置改变时产生的不平衡输出很大,考虑该因素整定定值将使保护灵敏度很低,实际上可以在线估计抽头位置[17]或将抽头位置信息引入微机保护[18],这样确定保护定值时就可以不考虑该因素的影响,这里仅考虑参数计算误差和CT变换误差的影响,取可靠系数为1.2,可得电压差动保护中幅值和相位判据定值分别为:Uset=34.8 V、θset=6.6°。该组定值完全可以保证在变压器任何正常状态下保护不会误动。
变压器内部发生故障时,回路方程不再成立,此时两侧补偿电压的幅值和相位都将出现较大的变化,表2给出了内部故障时,电压差动保护的计算结果。故障状态包括不同匝数的匝间故障、不同位置的相间故障和接地故障,仅对故障相的结果进行统计。
从表2可以看到,当发生严重内部故障(如相间短路)时,两侧补偿电压的幅值和相位间存在很大的差值,该保护的两个判据都能满足,当发生轻微故障(如小匝数匝间故障)时,补偿电压的幅值差可能小于定值,但是相位差仍大于定值,此时保护也能正确动作。
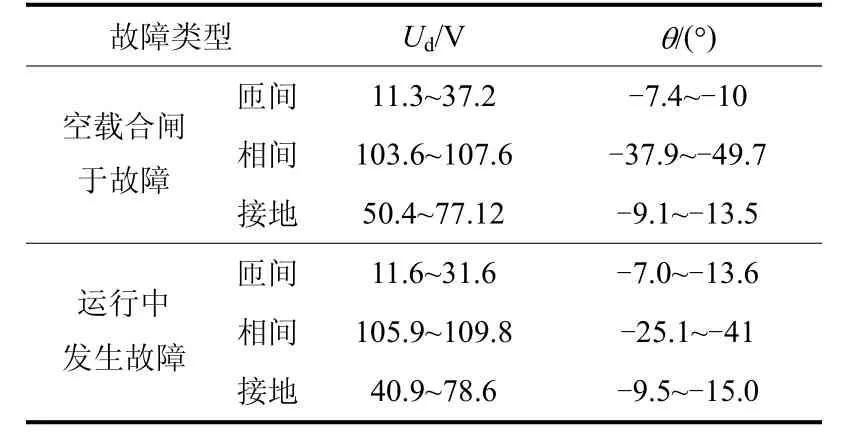
表2 内部故障时电压差动保护的计算结果Table 2 The results of voltage differential protection under internal fault conditions
为了直观地说明保护的性能,图9给出了匝间故障时保护计算结果在电压平面上的分布情况。图中扇形区外为动作区,可见由于引入相位判据,扩大了保护的动作区,可以保证保护在轻微匝间故障时可靠动作。
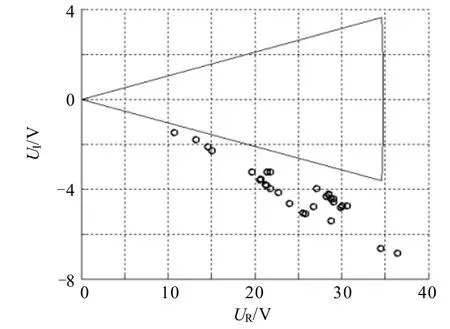
图9 内部轻微匝间故障时电压差动保护的计算结果Fig. 9 Results of voltage differential protection under internal slight turn-to-turn fault conditions
在保护的实现过程中,差动电压幅值计算量较小,因此首先计算差动电压幅值,如果幅值判据成立,直接判断变压器处于内部故障状态,否则再计算补偿电压相位差,当两个判据均不成立时判断变压器处于正常状态。这样即可保证严重故障时快速动作,又可保证轻微故障时可靠动作。
5 结论
本文在正常变压器回路方程的基础上定义补偿电压的概念,深入分析几种不利条件对变压器两侧补偿电压间幅值和相位关系的影响,在此基础上构建了综合补偿电压幅值和相位特征的电压差动保护。该保护反映了变压器正常与内部故障状态的本质区别,理论上励磁涌流时保护的输出为零,无需励磁涌流识别判据;综合了补偿电压幅值和相位特征,在保证保护可靠性的前提下提高了内部故障时保护的灵敏度;受变压器漏感参数计算误差影响很小,可以在变压器短路实验的基础上,按总漏电感的一半确定各侧线圈的漏电感,方便了保护的应用。分析结果表明了该保护的正确性和可行性。需要指出的是如果变压器空载合闸时不能测量负载侧电压,则该保护将失效,因此该保护的实用化还需进一步研究。
[1] 王维俭. 电气主设备继电保护原理与应用[M]. 2版.北京: 中国电力出版社, 2002.
[2] 王维俭. 变压器保护运行不良地反思[J]. 电力自动化设备, 2001, 21(10): 1-3.WANG Wei-jian. Consideration of improper operation of transformer protection[J]. Electric Power Automation Equipment, 2001, 21(10): 1-3.
[3] 王雪. 基于 Prony分析的励磁涌流识别方法[J]. 继电器, 2007, 35 (6): 1-4.WANG Xue. An inrush current identification method based on Prony analysis[J]. Relay, 2007, 35(6): 1-4.
[4] 黎功华. 基于人工神经网络模型的变压器保护原理[J].电力系统保护与控制, 2010, 38(10): 26-30.LI Gong-hua. Transformer protection principle based on the artificial network model[J].Power System Protection and Control, 2010, 38(10): 26-30.
[5] 马静, 王增平, 吴劼. 利用基波幅值变化特征快速识别励磁涌流和故障电流[J].电工技术学报, 2009, 24(6):166-171.MA Jing, WANG Zeng-ping, WU Jie. A novel method to rapidly identify inrush current and internal fault current based on variation characteristic of fundamental current amplitude[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 166-171.
[6] Eissa M M. A novel digital directional transformer protection technique based on wavelet packet[J].IEEE Trans on Power Delivery, 2005, 20(3): 1830-1836.
[7] 张荣海, 熊小伏, 夏莹. 基于模糊信息检索的变压器差动保护[J]. 电力系统保护与控制, 2010, 38(16): 132-136.ZHANG Rong-hai, XIONG Xiao-fu, XIA Ying. Power transformer differential protection based on fuzzy information retrieval[J]. Power System Protection and Control, 2010, 38(16): 132-136.
[8] 王增平, 高中德, 张举, 等. 模糊理论在变压器保护中的应用[J]. 电力系统自动化, 1998, 22(2): 13-16.WANG Zeng-ping, GAO Zhong-de, ZHANG Ju, et al.Application of fuzzy set theory in transformer protection[J]. Automation of Electric Power Systems, 1998, 22(2):13-16.
[9] Yabe K.Power differential method for discrimination between fault and magnetizing inrush current in transformers[J].IEEE Trans on Power Delivery,1997,12(3):1109-1118.
[10] 王增平, 徐岩, 王雪, 等. 基于变压器模型的新型保护原理的研究[J]. 中国电机工程学报, 2003, 23(12): 54-58.WANG Zeng-ping, XU Yan, WANG Xue, et al. Study on the novel transformer protection principle based on the transformer model[J]. Proceedings of the CSEE, 2003,23(12): 54-58.
[11] 郝治国, 张保会, 褚云龙. 基于等值回路平衡方程的变压器保护原理[J]. 中国电机工程学报, 2006, 26(10):67-72.HAO Zhi-guo, ZHANG Bao-hui, CHU Yun-long. Study on transformer protection principle based on equivalent circuit equilibrium equation[J]. Proceedings of the CSEE,2006, 26(10): 67-72.
[12] 王增平, 马静. 基于等效瞬时漏感与回路方程的变压器保护原理[J]. 中国电机工程学报, 2007, 27(19): 39-44.WANG Zeng-ping, MA Jing. A novel principle of transformer protection based on equivalent instantaneous leakage inductance and loop equation[J].Proceedings of the CSEE, 2007, 27(19): 39-44.
[13] 王雪, 王增平. 基于有限元法的变压器电感参数计算方法的研究[J]. 电力系统保护与控制, 2009, 37(24):11-14.WANG Xue, WANG Zeng-ping. An investigation on transformer inductance calculation based on finite element method[J]. Power System Protection and Control,2009, 37(24): 11-14.
[14] Nagpal M, Martinich T G., Moshref A, et al. Assessing and limiting impact of transformer inrush current on power quality[J]. IEEE Trans on Power Delivery, 2006,21(2): 890-896.
[15] Martinez J A, Walling R, Mork B A, et al. Parameter determination for modeling system transients-part III:transformers[J]. IEEE Trans on Power Delivery, 2005,20(3): 2051-2062.
[16] 王雪, 王增平. 变压器内部故障仿真模型的设计[J].电网技术, 2004, 28(12): 50-52.WANG Xue,WANG Zeng-ping. Study of simulation of transformer with internal faults[J]. Power System Technology, 2004, 28 (12): 50-52.
[17] 黄大为, 韩学山. 有载调压变压器抽头位置在线估计的实用算法[J]. 东北电力学院学报, 2001, 21(3): 9-13.
[18] Ahmed Y, Al-Mously S I. Sensitivity improvement of the digital differential relay for internal ground fault protection in the power transformer with tap changer[J].2001 IEEE Proto Power Tech Conference, 10-13, Sep.Porto, Portugal.

