基于主成分分析的神经网络动态集成风功率超短期预测

何 东，刘瑞叶

（哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001）

0 引言

准确的风功率预测是提高风电接入容量、电网运行稳定性和经济性的有效手段。具体来讲，准确的风功率预测可以用来安排电厂发电计划、保持电网功率平衡，并作为电网操作和电网阻塞管理的可靠依据。因此，实际生产急需提高风功率预测准确性。目前，用于风功率预测的方法主要有物理模型和统计模型（最小平方回归、神经网络等）。对于物理模型法，丹麦、德国、西班牙等国有预测系统投入运行，如 Prediktor[1]、Previento[2]与 LocalPred-RegioPred[3]等。其优点是无需大量的、长期的测量数据，更适用于复杂地形；缺点是需分析复杂的物理特性，如果模型建立的比较粗糙，则预测精度差。而统计方法虽然需要长期测量数据和额外的训练，但是能自动适应风电场位置，减小系统误差。相对其他统计方法，文献[4-7]的研究表明神经网络有很强的鲁棒性和容错性，更适用于处理像风功率预测这样的复杂非线性和不确定的问题。

使用神经网络预测首先要确定哪些变量作为输入。由于风功率影响因素复杂，主要有风速、风向、温度、气压、温度、湿度和地表显热等，若全部作为神经网络输入变量，则会导致神经网络计算效率低。文献[8]则指出，气压、温度和湿度这三个变量和风功率的相关性较小，故可以忽略这三个变量的影响；文献[9]引入了气压、温度和湿度这三个变量做为风电功率预测输入变量；文献[10]采用风速和温度进行预测。这些预测方法各有特色。实际应用中，可以使用平均影响值等方法找到对结果影响较大的变量，对不同的风电场数据找出的变量一般不同，因此所找出的变量缺乏普遍性。而直接忽略某个因素可能会给风功率预测带来误差。为减少变量数目，并尽量减少因此而产生的误差，本文采用主成分分析的方法来确定所需的最小变量数量。该方法适用于涉及变量数多，变量之间相关性明显的情况。

另外，用于风电场功率预测的神经网络实质是基于其在训练样本集上的误差极小化，而预测效果（推广能力）应由在训练样本集以外的检验样本上的误差来度量。但有时小的训练误差并不一定对应于小的预测误差，也就是所谓的“过拟合”现象，此时神经网络的泛化能力较差，进而导致预测精度的不稳定。本文采用神经网络动态集成方法实现风功率预测，避免“过拟合”现象。

1 基于主成分分析法的数据处理

影响风电场输出功率的气象因素有风速、风向、气温、气压和湿度等。为了既减少神经网络输入变量个数提高计算效率，又不影响预测精度，本文采用主成分分析法（principal components analysis ，PCA）将上述多个气象变量转化为少数几个主成分（即综合变量）。主成分之间互不相关，这些主成分既能反映原始变量的大部分信息，所包含的信息又不互补重叠。

1.1 主成分分析基本原理

主成分分析一般从总体协方差或是总体相关系数出发求解主成分。实际问题中，总体X的协方差矩阵Σ往往是未知的，需要由样本进行估计。设1x，为取自总体X的样本，每个样本有 p个指标，故任一样本ix可以表示为 p维向量，即其中任一元素的表示描述该样本的一个指标。样本表示为

记样本协方差矩阵S为

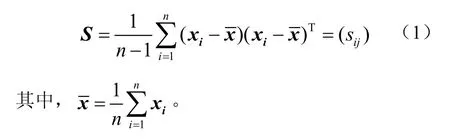
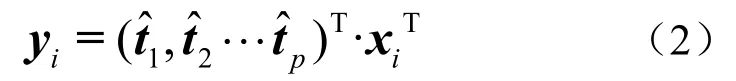
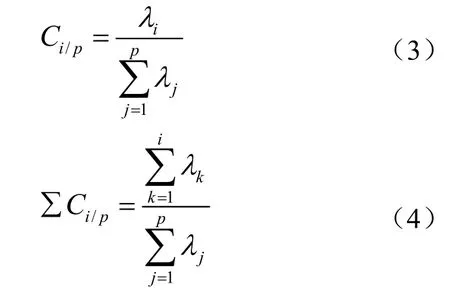
当积累贡献率大于某一设定值时，前i个成分称为主成分。

1.2 基于PCA的数据处理

本文采用的是南方某风电场2011年的数据，其i时刻测风塔测量值表示为其中风速1ix、风向2ix、气温3ix、气压4ix 、湿度5ix。

首先，根据 GB/T18710-2002中主要参数的合理范围和合理变化范围，剔除坏数据，并用上一时刻的数据代替。

然后，根据文献[11]，发现下 1个小时的风功率与前4个小时的历史数据相关。故用前4 h的历史数据来预测下1 h的风功率。

最后，将样本归一化并使用主成分分析将历史数据压缩。

设iy为得到的新样本。则有

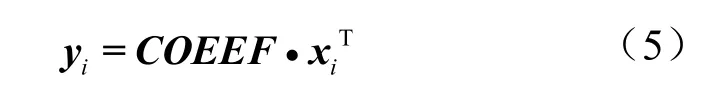
从式（5）看出各主成分为风速、风向、气温、气压、湿度的线性组合。虽然没有直接的物理含义，但是包含了这些气象数据的所有信息。

根据公式（3）计算贡献率得出各主成分贡献率如表1。

表1 各个主成分贡献率Table 1 Contribution rates of principal components

按公式（4）计算可知前3个主成分的贡献率累加已经达到98.2%。所以只需前3个主成分作为神经网络集成的输入即可满足要求。

处理之前每一时刻有6个气象参数，而处理之后每一时刻只有3个主成分作为参数。并且这3个参数都包含有原来5个参数的信息。这就在保证精确度的情况下，提高了神经网络的计算效率。另外这种方法有客观性和普遍性。

2 单个BP神经网络预测模型

BP神经网络也称为误差反向传播神经网络。根据文献[12]，本文单个神经网络采用单隠层设计。隐含层的神经元为非对称的tansig函数，输出层为purelin线性函数，训练方法为Levenbery-Marquardt优化法。

3 BP神经网络动态集成预测

将多个单个BP神经网络按一定方式训练，并将它们的预测结果集成起来，就得到BP神经网络集成。这样的网络集成能使其中的各个单个BP网络有一定的差异，从而提高整个BP网络集成的泛化能力，进而提高预测精度。

多神经网络集成可以简化网络设计，节省训练时间，并且提高学习正确率。

输入i时刻前4个小时主成分时间序列{yi-3, yi-4yi-2, yi-1, yi}(i = 1 ,,n )与其对应的i时风功率时间序列Pi(i = 1 ,,n )作为训练样本。样本分布 Dt初始化，各样本权值相同即初始为均匀分布。假设共有 T个单个神经网络，对于t = 1 ,,T 执行以下操作：

（1）用分布 Dt训练单个网络t，并得到预测风速th。

4 算例分析

本文算例的预测误差采用最大绝对相对误差（MAE）和平均绝对相对误差（MAPE）表征[13-16]。计算公式如下

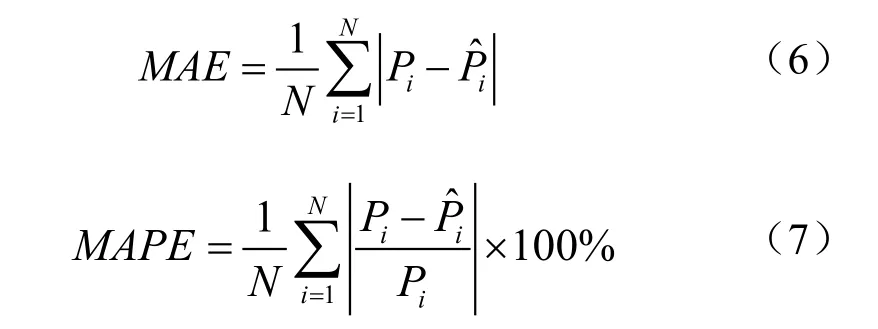
以南方某风电场为例进行验证。该风电场现安装风力发电机33台。每台600 kW，总装机容量19.8 MW。自1998年并网以来，以每10 min对风电场各气象参数及输出功率采样一次。本文截取其2011年3月份数据为例进行测试。集成10个单个BP神经网络，以预测起始时刻前1天144个采样点数据作为训练样本，预测起始时刻后3小时的风功率。

为验证基于PCA的数据处理的有效性。通过分别将全部气象参数、部分气象参数和基于PCA的主成分作为神经网络集成的输入，对南方某风电场2011年3月份风功率进行了仿真分析。结果如表2。

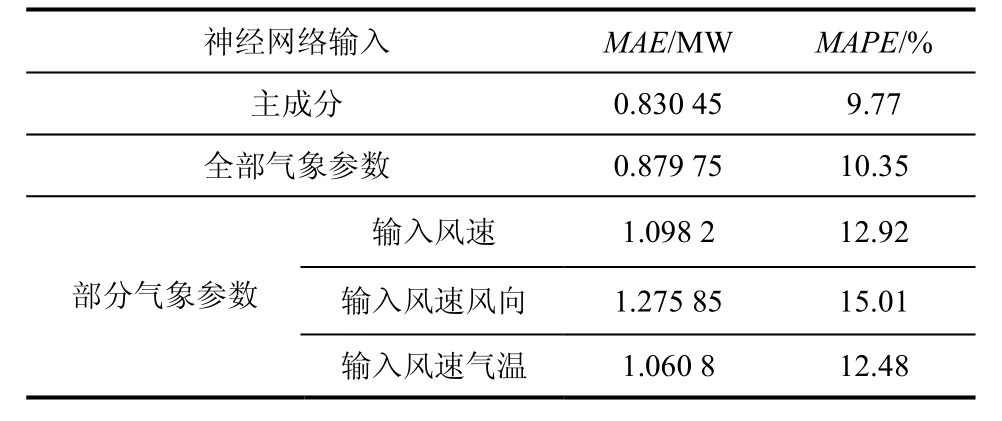
表2 不同输入预测结果误差对比Table 2 Different inputs prediction errors

结果表明采用基于PCA的数据处理，相对于全变量和部分变量分析，非但没有降低预测精度，反而有所升高。另外，其输入变量相对于全变量少，具有一定的高计算效率优势。

此外还比较了单个BP神经网络和BP神经网络动态集成。BP神经网络集成由10个单个网络组成。每个单个网络的训练误差为0.1%，最大迭代次数为1000次。结果发现通过上述BP神经网络集成的预测结果MAE为0.83 MW，MAPE为9.77%。与单个BP神经网络最好预测精度，MAE为1.04，MAPE为12.26%相比有了较大提高。

典型的如图1所示对2011年3月12日10点至13点的预测结果比较，表3是具体数据。

表3 单个BP网络与BP网络集成预测比较Table 3 Single BP net and BP net ensemble prediction MW

5 结语

本文采用基于主成分分析法对观测变量降维，能够客观地反映影响风功率预测的各种影响因素并提高计算效率。用神经网络集成，从原理和实际预测上都提高了预测精度。

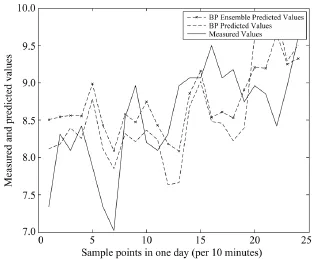
图1 单个BP网络与BP网络集成预测比较Fig. 1 Single BP net and BP net ensemble prediction

[1] Landberg L. Short-term prediction of local wind conditions[D]. Roskilde: Risø National Laboratory, 1994.

[2] Focken U, Lange M, Waldl P．Previento-a wind power prediction system with an innovative up scaling algorithm[C] // 2001 European Wind Energy Association Conference EWEC’01, Copenhagen, Denmark, 2001．

[3] Marti Perez I. Wind forecasting activities[C] // The First IEA Joint Action Symposium on Wind Forecasting Techniques, Norrkoping, Sweden, 2002．

[4] Kariniotakis G, Stavrakis G, Nogaret E. Wind power forecasting using advanced neural network models[J].IEEE Trans on Energy Conversion, 1996, 11(4): 762-767.

[5] Damousis I G, Dokopoulos P. A fuzzy expert system for the forecasting of wind speed and power generation in wind farms[C] // Proceedings of the PICA 2001 (The 22nd International Conference on Power Industry Computer Applications), IEEE Power Engineering Society, 2001: 63-69.

[6] Barbounis T G, Theochairs J B, Alexiadis M C, et al.Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE Trans on Energy Conversion, 2006, 21(1): 273-284.

[7] Ranirez-Rosado L J, Fernández-Jiménez L A, Monteiro C.Artificial neural network models for wind power short-term forecasting using weather predictions[C] //Proceedings of the 25th IASTED International Conference on Modeling, Identification, and Control.Anaheim, ACTA Press, 2006: 128-132.

[8] Thanasis G B, Theocharis J B. Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE Trans on Energy Conversion,2006, 21(1): 273-284.

[9] Fan S, Liao J R, Yokoyama R, et al. Forecasting the wind generation using a two-stage network based on meteorological information[J]. IEEE Trans on Energy Conversion, 2009, 24(2): 474-482.

[10] Potter C W, Negnevitsky M. Very short-term wind forecasting for Tasmanian power generation[J]. IEEE Trans on Power Systems, 2006(21): 965-972.

[11] 杨秀媛, 肖洋, 陈树勇．风电场风速和发电功率预测研究[J]．中国电机工程学报, 2005, 25(11): 1-5.YANG Xiu-yuan, XIAO Yang, CHEN Shu-yong. Wind speed and generated power forecasting in wind farm[J].Proceedings of the CSEE, 2005, 25(11): 1-5.

[12] 董安正, 赵国藩. 人工神经网络在短期资料风速估计方面的应用[J]. 工程力学, 2003, 20(5): 10-13.DONG An-zheng, ZHAO Guo-fan. Applications of artificial neural networks in wind speed estimation from short-term records[J]. Engineering Mechanics, 2003,20(5): 10-13.

[13] 王丽婕, 廖晓钟, 高阳, 等. 风电场发电功率的建模和预测研究综述[J]. 电力系统保护与控制, 2009, 37(13):118-121.WANG Li-jie, LIAO Xiao-zhong, GAO Yang, et al.Summarization of modeling and prediction of wind power generation[J]. Power System Protection and Control, 2009, 37(13): 118-121.

[14] 牟聿强, 王秀丽, 别朝红, 等. 风电场风速随机性及容量系数分析[J]. 电力系统保护与控制, 2009, 37(1):65-70.MU Yu-qiang, WANG Xiu-li, BIE Zhao-hong, et al.Analysis of wind speed probability distribution and wind turbine generator capacity factor[J]. Power System Protection and Control, 2009, 37(1): 65-70.

[15] 吴兴华, 周晖, 黄梅. 基于模式识别的风电场风速和发电功率预测[J]. 继电器, 2008, 36(1): 27-32.WU Xing-hua, ZHOU Hui, HUANG Mei. Wind speed and generated power forecasting based on pattern recognition in wind farm[J]. Relay, 2008, 36(1): 27-32.

[16] 武小梅, 白银明, 文福拴. 基于 RBF 神经元网络的风电功率短期预测[J]. 电力系统保护与控制, 2011,39(13): 118-121.WU Xiao-mei, BAI Yin-ming, WEN Fu-shuan.Short-term wind power forecast based on the Radial Basis Function neural network[J]. Power System Protection and Control, 2011, 39(13): 118-121.