双金属材料圆板Ⅲ型界面裂纹的ANSYS分析

金誉辉，金长义，陈金梅，张晓斌

（1.广西特种设备监督检验院，广西 南宁530219；2.广西工业职业技术学院，广西 南宁530003）

随着材料科学的迅速发展，双金属材料在工程上的应用日益增多。但由于材料界面裂纹往往成为影响材料整体力学行为的重要因素，使双金属材料强度下降，因而对各种不同类型双金属材料界面裂纹扩展的研究具有非常重要的意义。

目前，对于断裂力学裂纹扩展问题有两种不同的观点：一种应力强度的观点，认为裂纹尖端的应力强度因子超过表征材料特性的临界应力强度因子时，裂纹发生失稳扩展；另一种是能量观点，认为当裂纹的扩展使得释放的弹性能多于产生新裂纹所需要的能量，则发生裂纹的失稳扩展。这两种观点有一定的联系。由相关的基础知识可以看出，应力强度因子与裂纹尖端领域内点的坐标无关，只是表征裂纹体弹性应力强度的量，而不表征各种裂纹变形状态下的应力分布，应力强度因子K是由裂纹的远场边界条件确定，所以一般来说，与受载荷方式、荷载的大小、裂纹长度及裂纹体的形状有关，当然有时候与材料的弹性性能也有关。求解应力强度因子的方法有三种：解析法、数值解法和实验方法，基本思路均为由弹性或者是塑性方程出发，把裂纹作为一种边界条件，考察裂纹尖端的应力场、应变场、位移场，设法建立这些场与控制断裂的物理参量之间的关系和裂纹尖端附近的局部断裂条件，从而获得应力强度因子的值[1~2]。本文通过数值解法采用三维有限元软件ANSYS来分析了双金属材料圆板Ⅲ型界面裂纹的应力场、应变场、位移场。

1 问题描述

图1所示为带有Ⅲ型界面中心裂纹双金属材料圆板[3]，其中圆板上下两种材料均为各向同性，至少有一种为脆性材料。圆板半径R，板上有一随时间变化的界面中心裂纹2α（t）。以圆板中心为原点建立柱坐标系，与圆板面垂直的方向为z轴方向。板面上的任意点均由r和θ确定。界面上下两种材料的剪切弹性模量和密度分别为G1、ρ1和G2、ρ2。圆板周边自由。界面中心裂纹表面作用反平面剪应力-τ，形成自平衡体系。裂纹沿界面稳态扩展。板上只有z方向位移W（r，θ，t），其为r，θ，t的函数。

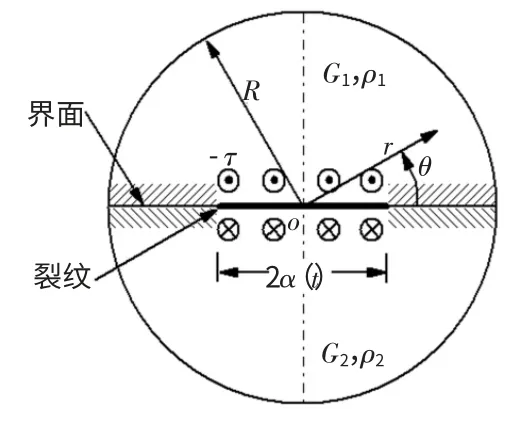
图1 具有Ⅲ型界面裂纹的圆盘

本文采用三维有限元软件ANSYS来分析双金属材料圆板Ⅲ型界面裂纹的扩展。整个分析主要有两个步骤：

（1）求解裂纹尖端的应力场、应变场、位移场，这部分内容ANSYS求解已经相当成熟；

（2）利用第一部分求解出的结果，像边界上求出的应力、应变、位移来求解应力强度因子[4~5]。

2 计算实例

如图1所示，根据对称性，取一半进行分析。所选用金属材料1和材料2中至少有一种为脆性材料，两种材料采取对接焊，焊接处的强度290~310 MPa。己知两种金属材料的工程常数及相关尺寸 受力如表1、表2所示。

表1 材料常数

表2 其它参数

2.1 建立模型

在远离裂纹尖端时，选用普通的SOLID45单元，裂纹尖端处，选用20节点的SOLID95单元，由于不能采用ANSYS命令KSCON来直接生产1/4单元，所以就采用APDL语言编程来直接生成网格模型，共生成了1296个节点、520个单元，生成的3D有限元断裂模型[6~7]，如图2所示。

图2 有限元模型

2.2 加载计算

2.2.1 加载

（1）约束荷载：在对称面处只施加约束X方向位移的对称约束载荷，在和裂纹面同一平面上远离裂纹的一端施加约束各个方向的自由度的约束载荷。

（2）外加荷载：将在裂纹面上的面载荷，转化到每个节点的集中荷载，转化后在裂纹面上靠近外侧处的每个节点加绝对值为152.4 N的集中力，如图3所示。

图3 加载后的模型图

2.2.2 计算

通过计算可以得到圆板变形前后对比图，各个场的等值线图，裂纹尖端的应力场和位移场，以及应力强度因子等。

（1）双金属材料圆板变形前后对比图，如图4所示。

图4 变形前后对比图

（2）Z方向位移的等值线图，如图5所示

图5 Z方向位移等值线图

（3）应力场：得到了τyz的应力等值线图，如图6所示，同时为了能和前面的计算结果进行比较，继续将ANSYS分析所得结果绘制成曲线图，得到了以裂纹尖端为圆心，离裂纹尖端距r1=1.104 1 mm、t=0.1 s情况下的应力场－转角（θ1）的关系图，如图7所示。其中θ1表示为以裂纹尖端为原点的极坐标的极角。

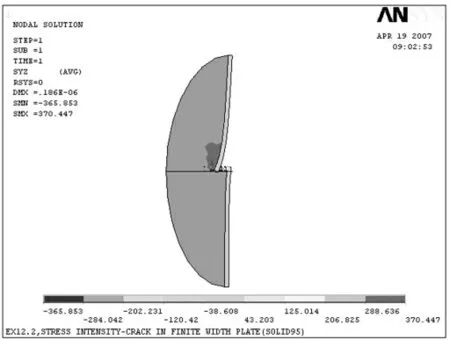
图6 τyz的应力等值线图

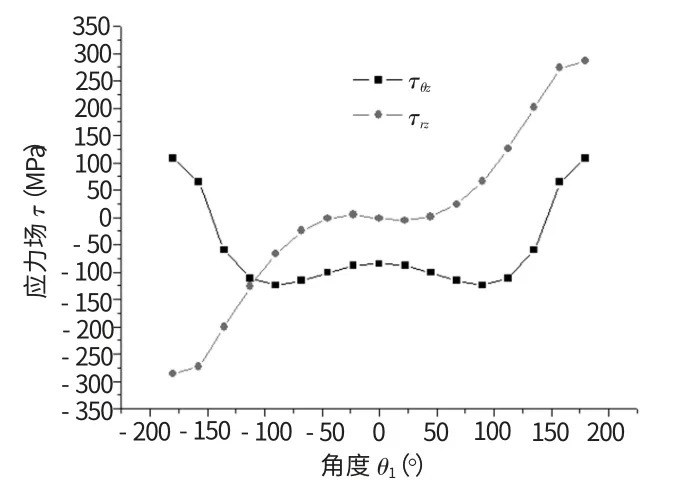
图7 r1=1.104 1 mm、t=0.1 s时，应力场－转角（θ1）曲线图

（4）位移场：将位移场随参数而变化的情况绘制曲线图，分以下三种情况：

一是，在r1=1.104 1 mm、t=0.1 s情况下，位移－转角（θ1）的关系图，如图8所示。

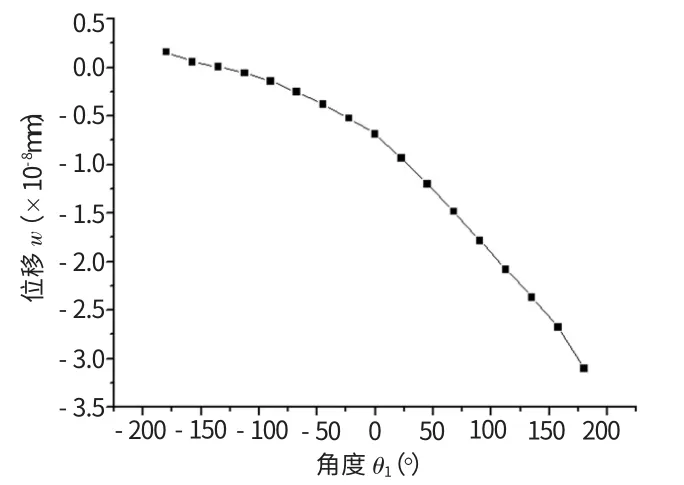
图8 r1=1.104 1 mm、t=0.1 s时，位移－转角（θ1）曲线图

二是，在θ=0°，t=0.1 s下，位移－半径（r）的关系图，如图9所示。

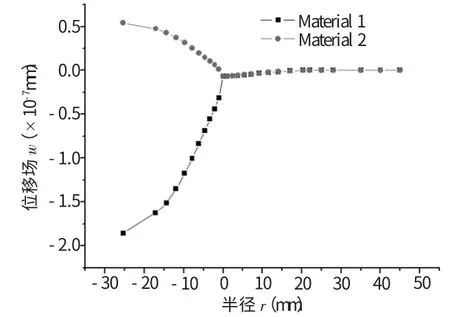
图9 θ=0°，t=0.1 s时，位移－半径（r）的曲线图

三是，在θ=90°，t=0.1 s下，位移绝对值－半径（r）的关系图，如图10所示。

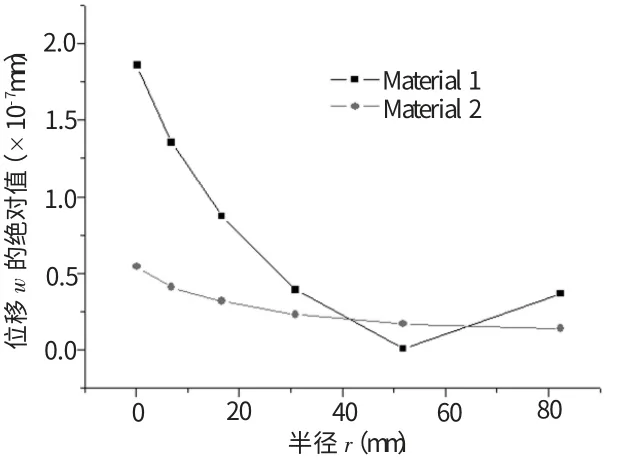
图10 θ=90°，t=0.1 s时，位移绝对值－半径（r）的曲线图

（5）应力强度因子

分析了应力强度因子随裂纹长度的变化，将得到的数据制成了相应的曲线图，如图11所示。

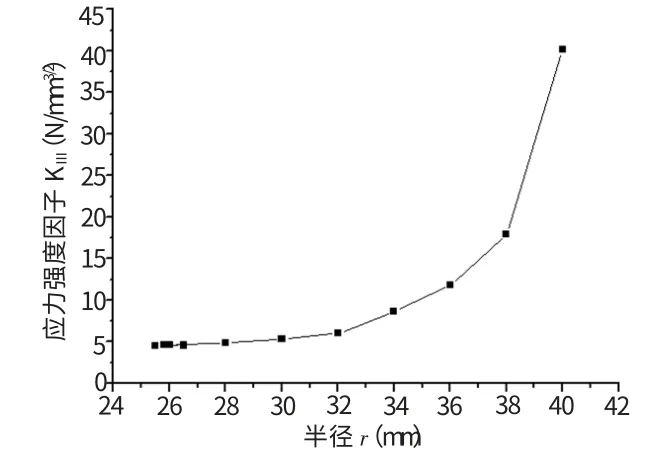
图11 应力强度因子－半径（r）的曲线图

3 结果分析

通过ANSYS分析得到的双金属材料圆板Ⅲ界面裂纹尖端的应力场、应变场和位移场及应力强度因子，我们可以得出以下结果：

（1）已知圆板Ⅲ型界面焊接街头处的强度为290~310 MPa，根据图6的应力场可知，能保证圆板Ⅲ型界面裂纹动态扩展。

（2）应力场：从图7中可以看出，裂纹尖端应力场随着角度的不同而变化。

对于τθz来说，在裂纹尖端和上下裂纹面三处都出现了τθz达到最值，即图中所对应的θ1=180°表示的是材料1在裂纹面的上表面，而θ1=0°指的是裂纹尖端的界面处，而θ1=-180°就是裂纹面的下表面，显然，根据应力集中的理论知识可知，对于任何几何形状有突变的地方都将产生应力集中，而在裂纹尖端处，考虑在弹性力学上，应力可以是无穷大（称为应力奇异性，即应力集中很大），定性的说明了为什么层板材料破坏时，大多数破坏都是从层与层结合界面端部开始的。根据裂纹尖端的应力奇异性知，裂纹尖端的应力应该达到无穷大，实际7中表明裂纹尖端的应力集中系数最大也没超过15，说明了裂纹尖端存在塑性屈服。

对于τrz来说，出现最值的点也是和τθz一样出现在裂纹的上下表面，所不同的是，在裂纹的界面上，τrz的值接近于0，根据理论知识裂纹界面处指的是θ1=0°，显然τrz等于0，而ANSYS的结果正好也验证了这一点。

（3）位移场：图8裂纹尖端位移随角度θ1的变化关系图，从图中知，曲线上方表示的是材料2随角度变化的位移，下方表示的是材料1相应的位移，在各自材料内的位移都没有太大区别，区别主要是两种材料到界面的角度相等时，材料2的变形小于材料1的变形，这一点是因为材料2的剪切模量大于材料1的剪切模量所引起的；在界面处，当裂纹还没有传播到的地方，此时裂纹并没有开裂，曲线在此处是连续的；裂纹传播到的地方，也就是说裂纹在此处已经开裂了，那么材料1和材料2在界面处已分离，则使得到的曲线在界面处应该是不连续的，由于材料1和材料2的位移方向是相反的，所以图中并没有显示出来。若将位移表示成绝对值时，则在界面处将会出现位移绝对值的突变值。

图9描述的是界面位置不同时相应的位移值，在裂纹面内，两种材料是分离的，材料1和材料2的位移最大值都是出现在圆板中心点处，此时r=0，且随着r的增大而减小；等到了裂纹尖点时，此时正是裂纹开裂的临界位置，材料1和材料2的位移值相等，且等于零。

图10表述的是位移随半径的变化曲线，这里半径r是在垂直裂纹面方向的变化。沿着半径方向时，材料1的位移方向是向Z的负方向，材料2是向正Z方向，r增大到一定值时，材料1的位移开始反向，材料1的位移方向变为Z的正方向，而材料2的位移方向一直是正方向，原因是材料2的剪切模量更大引起的。当然两种材料的位移都是随着r的增大而减小。

（3）应力强度因子：文献[3]给出了双金属材料圆板Ⅲ型界面裂纹的应力场、位移场的理论解，却没有给出应力强度应子的解析解。本文通过ANSYS的分析结果，得到了应力强度应子的数值解，为以后通过实验来修正应力强度因子做准备。图11描述的是裂纹扩展时的动态应力强度因子与半径的关系，事实上这里的半径是指裂纹在某时刻扩展到某位置时裂纹长度的一半，显然在静态断裂问题中，应力强度因子只是裂纹长度和外力的函数。曲线图正确地反映了应力强度因子随半径的变化而变化，随着裂纹的扩展，裂纹长度逐渐增大，应力强度因子也相应的增大。

4 结束语

本文分析得到的双金属材料圆板Ⅲ型界面裂纹尖端的应力场、应变场和位移场及应力强度因子的数值解，为认识双金属材料圆板Ⅲ型界面裂纹扩展机理提供理论依据。在研究双金属材料Ⅲ界面裂纹的应力强度应子的时候，解析解存在着局限性。而数值法为双金属材料圆板Ⅲ型界面裂纹的应力强度因子的解析解提供了修正依据。

[1]田宗若.复合材料剪切型断裂力学研究[M].南昌:江西高校出版社，1994，8-23.

[2]张 行.断裂力学中应力强度因子的解法[M].北京:国防工业出版社，1992:10-105.

[3]金长义.材料圆板Ⅲ型界面裂纹扩展应力位移场[J].北京理工大学学报，2005，25(8):667-669.

[4]王水林，葛修润.有限元方法在模拟裂纹扩展中的应用[J].岩石力学与工程学报，1997，16(5):405.

[5]陈梦成，余荷根，汤任基.三维裂纹问题的高精度数值解法[J].固体力学学报，2002，23(2):207-211.

[6]张朝晖.ANSYS8.0结构分析及实例解析[M].北京:机械工业出版社，2005，478-495.

[7]祝效华，余志祥.ANSYS高级工程有限元分析范例精选[M].北京:电子工业出版社，2004，411-421.