变换群与若干哲学范畴的广谱分析
郭少磊
(华北水利水电大学 水利学院,郑州 450011)
【经管索微】
变换群与若干哲学范畴的广谱分析
郭少磊
(华北水利水电大学 水利学院,郑州 450011)
从广谱哲学的视角出发,可把变换群看成人的一种观控方式,从而把变换群、不变性与事物客观性三者联系起来;分析变换群与分类的内在联系,可引出差异与同一、共性与个性的变换群描述;运用广谱哲学的类变理论,可揭示变换群与量变质变规律、可推测与不可推测的数学机理。
变换群;哲学范畴;广谱分析
通常对变换群概念的理解主要限定在纯数学意义上,很少涉及到其事理和哲理。本文依据广谱哲学对变换群概念和方法的分析,探讨变换群与人的观控方式和事物的客观性,以及变换群诱导的差异与同一、共性与个性、量变与质变、可推测与不可推测等重要关系的意义。
一、变换群与观控方式
变换群是以变换为元素的群,通常的抽象群是满足4个条件(封闭性、结合性、单位元、逆元)的集合,但由于变换作为元素的特殊性,因此由变换构成群的条件仅需要2个。设G是变换的集合,*是变换之间的运算。若满足:(1)G中任两个变换的复合变换存在,且仍是G中的一个变换;(2)G中每个变换的逆变换存在,且仍是G中的一个变换;则(G,*)是一个变换群。

在广谱哲学中,变换被看成一类特殊的观控方式。[1]30-31观控方式即人们观察和控制事物的方式(角度、层次、方法、手段、条件等)。例如通常做实验就是先控后观,即把实验对象置于一个典型环境下进行观察。数学上的变换在操作意义上也表现为一定观控方式下的观察。例如解析几何中的坐标变换可以看做先旋转再平移的操作;给定一个几何对象(如三角形、圆等),看它在上述操作下,哪些性质变化,哪些性质不变,这就是先控后观的方式。此外,像仿射几何中的仿射变换、射影几何中的射影变换、拓扑学中的拓扑变换等,均可如是观。在经典力学中,伽利略变换代表了宏观低速条件下的观察方式,而狭义相对论的洛伦兹变换,代表了微观、高速条件下的观控方式。[1]41-42此外,广义相对论中任意参照系之间的变换、规范场论中的位相变换等,均有确切的观控意义。
把变换群的元素(变换)视为一定观控方式的观点,将为分析一般事物的机理打开新的视野。
二、变换群与事物的客观性
在广谱哲学中,研究对象的客观性被定义为:在一定的观控条件下,n个人或n次(n在理论上可以为无穷大)独立的观控结果具有一致性或不变性。进一步简化、抽象后,客观性即一定观控方式下n重观控结果的等价性。[1]当变换群的元素即变换被看成是一定的观控方式时,则变换群下的不变性便与研究对象的客观性联系起来了。例如,由形如(1)的所有变换构成一个变换群,称为运动群。容易验证,在变换(1)的作用下,一个平面图形的长度、角度均不变,因此该几何图形的形状和大小均保持不变。换言之,在旋转和平移的操作下,物体(这里是几何图形)的刚性不变。

这时,刚性就是旋转平移这种观控方式下的客观属性。又如伽利略变换构成一个变换群,称为伽利略变换群。不难验证,在伽利略变换下,时间间隔,空间间隔 (一物体的长度)以及牛顿力学定律都是不变的。换言之,在伽利略变换(反映宏观低速运动)这种观控方式下,时间不变、空间不变是自然界物质运动的客观属性,牛顿力学定律(如)是自然界物质运动的客观规律。同样,洛伦兹变换也构成一个变换群,称为洛伦兹变换群。可以证明,在洛伦兹变换下,上述的时间间隔、空间间隔要改变,但时空间隔不变,它反映了在洛伦兹变换(反映微观高速运动)这种观控方式下,时空相互联系的属性是一个客观属性。此外还可以证明,在洛伦兹变换下,在不同的惯性系,麦克斯韦方程组的形式是不变的,它反映了高速运动(电磁场运动)下电磁场规律的客观性。

把变换群、不变性、客观性这三个表面上不相关的概念联系起来,我们就能在科学观上得到一个深化:既然变换群下的不变性反映了事物的客观性,而一切科学都是研究一定事物一定层面的客观性的,因此,一切科学都是研究一定观控方式下一定事物一定层面的不变性的。[2]显然,这一结论给我们提供了透视各门科学的一个重要侧面。
三、由变换群诱导的若干重要关系
在数学上可以证明,给定集合X上的一个变换群G,可以诱导一个等价关系,从而决定了X的一个分类;反之,给定X上的一个分类,可以诱导X上的一个变换群G,即分类与变换群有着紧密的内在联系。[3]由这种联系,我们可以引出对认识论、本体论有重要价值的若干关系的广义量化模型。
(一)差异与同一的关系。
按照广谱哲学的观点,等价关系作为分类标准,也反映了一定的观控水平。例如,设A是人的集合,按“同性别关系”(等价关系),可以把A分成“男人类”和“女人类”;按照“同品德关系”(等价关系),可以把A分成“好人类”和“坏人类”,等等。显然,从性别上和品德上看人,代表两种不同的观控水平。当我们选定一种观控水平时,一个集合A就被分成若干个等价类,在同一个等价类内,所有的事物在等价关系(同一性关系)[4]的意义上视为无差别。但在不同的等价类之间,分处两个等价类的事物,视为有质的差别,这就引出了差异与同一的关系。
从数学上看,分类是一个映射fδ:→A/δ,其中A/δ={A1|i=1,2…,n},且当i≠j时,A1∩AJ=Φ(空集)。这时,所谓同一性是指,对∀x,y∈Ai,有(x,y)。所谓差异性是指,对∀x∈Ai,y∈Aj(i≠j),有(x,y)∈Ai×Aj,其中符号×表示笛卡尔直积。

图1 等价类对应变换群的轨道
上面讲的变换群可以诱导一个等价关系,实质上是说,对于集合A的任两个元素x,y∈A,变换群的一个变换g∈G,把x变成y,即g(x)=y,而这样一个关系是一个等价关系。原因在于变换群有恒等变换I∈G,它把任意的x∈A,变成x自身,即g(x)=x,这就导致自返性。其次,变换群的每个变换g∈G,存在逆变换g-1,使得当g(x)=y时,有g-1(y)=x,这就导致对称性。最后,由变换的复合可导致传递性。这就诱导了一个等价关系。通常把集合Ωx={g(x)|g∈G,x∈A}称为A在G作用下的轨道。容易知道,变换群作用在集合A上的效果是:它把由δ划分的每一类元素变成自己一类的元素,因此,变换群作用下的每一条轨道恰好是由δ划分出来的一个等价类(图1)。于是同一性与差异性转化成变换群的语言,这时所谓同一性是指,对∀x,y∈Ωx,有(x,y)∈;而差异性是指,对∀x∈Ωx,y∈Ωy,有(x,y)∈Ωx×Ωy,即同一条轨道上的两个事物具有同一性,不同轨道上的事物具有差异性。
(二)共性与个性的关系
当等价关系选定后,分类也可以从共性和个性的角度进行分析。不同等价类内的事物,在不具有等价关系的意义上没有共性。例如男人类和女人类各取一个元素,在不具有同性别的意义上,没有共性(虽然具有一般人的共性,那是另一种分类标准)。但在同一个等价类里,(x,y)∈A2(A1∈A/δ),它们在等价关系的意义上具有共性。这时任何x,y∈A1,有x≠y,这是各个事物的个性或特殊性。例如在男人类里,任何两个男人在长相、身高、肤色、体态等方面是各个不同的。显然,把等价类看成是变换群的轨道,有类似的结论。不过,用变换群的轨道描述共性和个性,更适于描述同一个事物的变化过程,即一个事物由x态变到x'态时,如果处在同一条轨道上,它们具有共性,但x≠x',又具有各自的特殊性。这就如同处在同一圆(旋转群的一条轨道)上的两点x和x',它们具有相同的半径(共性),但它们位置不同(特殊性或个性)。
(三)量变与质变的关系
如果考虑事物自身的发展变化可以划分为若干个阶段,则划分的标准成为沿时间方向展开的等价关系(广谱哲学称为自等价关系),它的实质是在一定时段内“保持事物的性质不变”。例如,水在0℃到100℃之间保持液态水不变,就是广义的量变,广谱哲学称为同类变,即在同一个等价类内的变化。但当达到100℃时,液态水变成汽态水,就是广义的质变,广谱哲学称为异类变,[2-5]即从一个自等价类跃迁到了另一个自等价类。

图2 从变换群轨道上看量变和质变关系
从变换群的角度看,上述按自等价关系的分类也对应一个变换群,称为自等价变换群,这个变换群的轨道生成诸自等价类。在图2中,((x,1),(x',t'))∈是在同一条轨道内变化,即广义的量变,而((x,t),(x',t'))∈Ω1×Ω2是从一条轨道Ω1跃迁到了另一条轨道Ω2,即广义的质变。[2]
一个典型的例子是社会上的等级现象(权力等级、职称等级、学历等级等),可以看成一种划分,其等价关系是“处在同一等级中”,这时每个等级是一个等价类,从而对应变换群的一条轨道。当一个人没有得到提升,始终处在同一个等级时,表现在同一条轨道上“滑行”(如从一个科级岗移到另一个科级岗),这是广义的量变。当他得到了提升,从一个较低的轨道跃迁到较高的轨道,或者他被降级,从较高的轨道跃迁到较低的轨道,就是广义的质变,如图3所示。

图3 等级现象中的量变和质变
(四)可推测与不可推测的关系
从认识论角度看,上述量变质变模型可用来研究人们如何推断过去和预测未来。推断过去是从现在推测过去,即“向后看”,预测未来是从现在推测将来,即“向前看”。广谱哲学认为,无论“向后看”还是“向前看”都要依据某种不变性(不变的性状或规律),称为“等价迁移条件”。[1]在图2中,由于((x,t),(x',t'))∈即t时刻x的性状与t'时刻x'的性状没有本质差别(处在同一条轨道即同一个等价类中),因此,可以从(x',t')的性状推出(x,t)的性状,反之亦然。例如,可以从人造地球卫星现在的位置(x',t')推出以前某时刻的位置(x,t),也可以从现在的位置(x,t)推出未来某时刻的位置(x',t')。其原因在于卫星处在同一条轨道(等价类)上。如果卫星突然变轨就无法做上述推测,这是因为等价迁移的条件遭到了破坏。
一般说,当事物的变化处在变换群的同一条轨道(同一个等价类内)时,可以依据不变性推断过去和预测未来,当事物的变化是由一条轨道跃迁到另一条轨道时,由于两条轨道之间不存在变换(注意前面讲的变换群把由δ划分的每一类元素变成自己一类的元素),因此上述推断与预测就不可能了。
不过,换个角度看,不可推测是由分类造成的。如果分类标准变了,则等价类的划分也变了,从而变换群的轨道也变了,如图4所示。
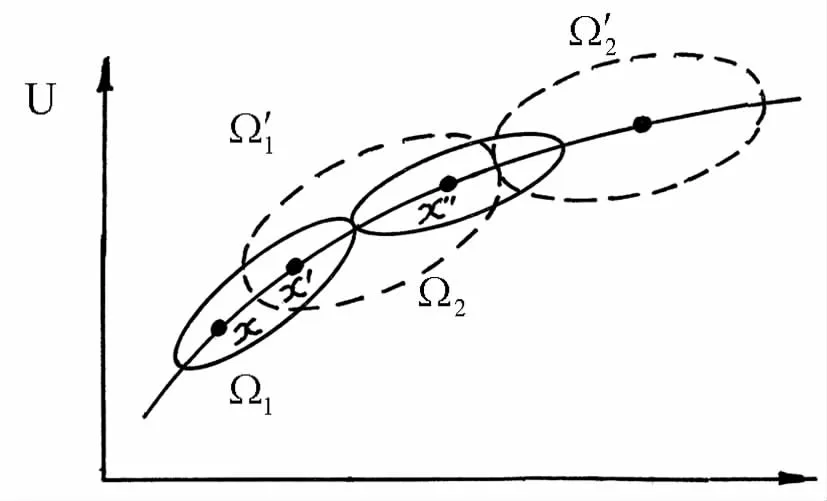
图4 从变换群轨道看可推测与不可推测关系
图4中,对于原轨道Ω1和Ω2而言,由于((x,t),(x',t'))∈,故从(x,t)到(x',t')或者反过来是可推测的。但由于((x,t),(x',t'))∈Ω1×Ω2,故从(x,t)到(x',t')或者反过来不可推测。对于新轨道Ω'1和Ω'2而言,由于((x',t'),(x',t'))∈,因此由(x',t')到(x',t')或者反过来是可推测的(注意对旧轨道不可推测)。这就是说,当分类标准改变时,可推测与不可推测具有相对性。
例如,我们从监控录相中锁定了犯罪嫌疑人的相貌特征。一般情况下,人的相貌特征在一定时段内是稳定不变的,可以看成在一个自等价类中。但若该犯罪嫌疑人做了重大的整容手术,则破坏了等价迁移条件,就无法推断该犯罪嫌疑人以前的相貌特征。不过,如果还提取了犯罪嫌疑人的DNA结构,由于DNA结构不会随相貌的改变而改变,它会在很长的时段(生前乃至死后)保持同构性(一种等价关系),因此可推断“此犯罪嫌疑人就是彼犯罪嫌疑人”。
四、结语
综上所论,变换群的概念经过结构分析(它与分类的联系),事理分析(它与观控方式、客观性的联系),哲理分析(它与异同关系、共性个性关系、量变质变关系、可推测与不可推测关系等的内在关联),展现了极深刻的内涵和广泛的意义。当把它的精髓概括为一定观控下的不变性时,它已不限于是一个纯数学的概念,而是成为我们观察现实、分析现实的一种重要的观控方式。
[1]张玉祥.广谱存在论导引[M].香港:香港天马出版有限公司,2004.
[2]张玉祥.广谱哲学在自然辩证法教学中的若干应用[J].华北水利水电学院学报:社会科学版,2009,(1):17-20.
[3]张尧庭.指标量化、序化的理论和方法[M].北京:科学出版社,1999:41-43.
[4]张玉祥.结构型数学及其在广谱分析中的应用[J].河南科学,2009,(5):525-529.
[5]王晓岗.关于哲学数学化的一些思考——从广谱哲学谈起[J].广西社会科学,2012,(9):32-35.
A Broad-spectrum Analysis on Transformation Group and Philosophical Catetories
GUO Shao-lei
(School of Water Conservancy,North China University of Water Conservancy and Hydroelectric Power,Zhengzhou 450011,China)
Based on broad-spectrum philosophy,transformation group is taken as ahuman observocontrol mode which connects transformation group with invariance and objectivity.An analysis on ingenerate connection between transformation group and classification makes expression of transformation group in terms of difference and identity,generality and individuality clear.The Class-change theory of broad-spectrum philosophy can reveal both the relationships between transformation group and qualitative and quantitative change and the mathematical mechanism of reference and non-reference.
transformation group;philosophical categories;broad-spectrum analysis
C02
:A
:1672-3910(2013)05-0084-04
2013-05-29
郭少磊(1982-),男,河北元氏人,北京林业大学博士生。

