一种改进的带修正因子模糊控制器的仿真应用

钱 宏，方康玲

（武汉科技大学 信息学院，湖北 武汉 430081）

模糊控制作为智能控制的一个重要分支，它综合了专家的操作经验，具有不依赖被控对象的精确数学模型、抗干扰能力强、响应速度快等特点，在工业控制中得到了极为广泛的应用[1]。但是常规模糊控制方法存在建立控制规则困难、有众多参数待定等缺点，并且不能消除系统的稳态误差。文献[2]介绍了一种带修正因子的模糊控制器，通过改变修正因子可以灵活改变控制规则。文献[3]提出消除模糊控制系统的稳态误差可以考虑在系统中加入积分环节。在此基础上本文提出了一种改进的带修正因子模糊控制器，并且用单纯形法对参数寻优进行初始化设置，仿真结果与传统的PID控制结果对比证明这种控制器产生的超调量小，能快速达到稳定，且抗干扰能力强，将算法移植到PLC对水箱液位进行控制，控制效果良好。

1 改进的带修正因子模糊控制器的设计思想

1.1 带修正因子模糊控制

基本模糊控制的关键在于建立一张满意的控制表，而这也是改进其控制品质的着眼点所在。为了简化推理过程，模糊控制规则可以采用带修正因子的解析形式，其解析式为U＝－＜α*E+（1－α）EC＞，式中α[0，1]，E＝＜Ke*e＞，EC＝＜Kec*ec＞。其中Ke，kec分别为误差和误差变化率的量化因子，＜＞表示四舍五入取整操作，E、EC分别为误差和误差变化率量化取整，U为控制量量化取整，α[0，1]称为修正因子，随着α值的改变，E和EC对U的贡献也在变化，从而改变模糊控制规则。但是一旦修正因子α选定，控制规则便固定了，虽然引入多个修正因子可以灵活地改变控制规则，但是随着修正因子个数的增加，也给寻优工作增加了难度[4]。

1.2 并联智能积分消除稳态误差

一般的模糊控制系统通常采用二维模糊控制器结构形式，它们以系统误差E和误差变化率EC为输入语言变量，因而具有类似于常规PD控制器的性能。为了消除误差常见的解决方法是在模糊控制中引入积分环节，积分环节添加在控制器不同地方产生的效果也不同，文献[5]说明全并联加入法是比较理想实用的形式。全并联加入法是由一个常规的积分器和一个模糊控制器相并联构成的，二者的输出量相叠加作为控制器的总输出，该方法可以有效消除稳态误差和极限振荡。

传统的引入积分环节方法存在积分作用针对性不强、积分参数设置不当易造成系统振荡等缺点，为了克服上述缺点，积分环节可以改进为智能积分，对系统误差选择性的积分。典型二阶阶跃响应曲线中，当e*ec＞0表示系统偏离平衡点，当e*ec＜0表示系统向平衡点靠近，经综合考虑，确定进行智能积分的条件为：当e*ec＞0或ec＝0且e≠0时，对误差进行积分；当e*ec＜0或e＝0时，不对误差进行积分，并联智能积分的设计如图1所示。

图1 并联智能积分Fig.1 Parallel intelligent integral

1.3 控制器的初始化设置

模糊控制器的初始化参数对控制性能的影响很大，当参数选取不当时可能引起系统的振荡甚至失控，本文采用单纯形法反复启发试验优化控制参数。单纯形法是一种多维直接搜索的局部优化方法，它在寻优过程中不必计算目标的函数梯度，只是针对一定图形的顶点按照一定规则来搜寻。其寻优思想是：在n维空间取（n+1）个点构成初始单纯形，比较这（n+1）个点处目标函数值的大小，这里可以选取目标函数J＝ITAE＝∫t|e（t）|d t，丢掉最坏的点（目标函数值最大的点），代之以新的点，构成新的单纯形，反复迭代，使其顶点处的函数值逐步下降，顶点逐步逼近目标函数的最小点。

2 系统仿真试验结果及分析

为了验证设计的模糊控制器的可行性，利用Matlab平台和Simulink仿真软件包仿真该控制器的性能，仿真模型如图2所示。图2上半部分为改进的带修正因子模糊控制器。控制对象为二阶延时模糊控制器规则的生成推导在模块‘tuili’中实现，智能积分判断条件在模块‘zhineng’中实现，上述控制器的待寻优参数有4个，分别为α0、αs积分作用系数K i和比例因子K u，其中α0、αs的寻优范围在[0，1]内。图2下半部分为目标函数（ITAE）的求取，各点目标函数值可以调用上面的仿真模块得到，单纯形法的寻优可以在Matlab平台编写M文件实现。

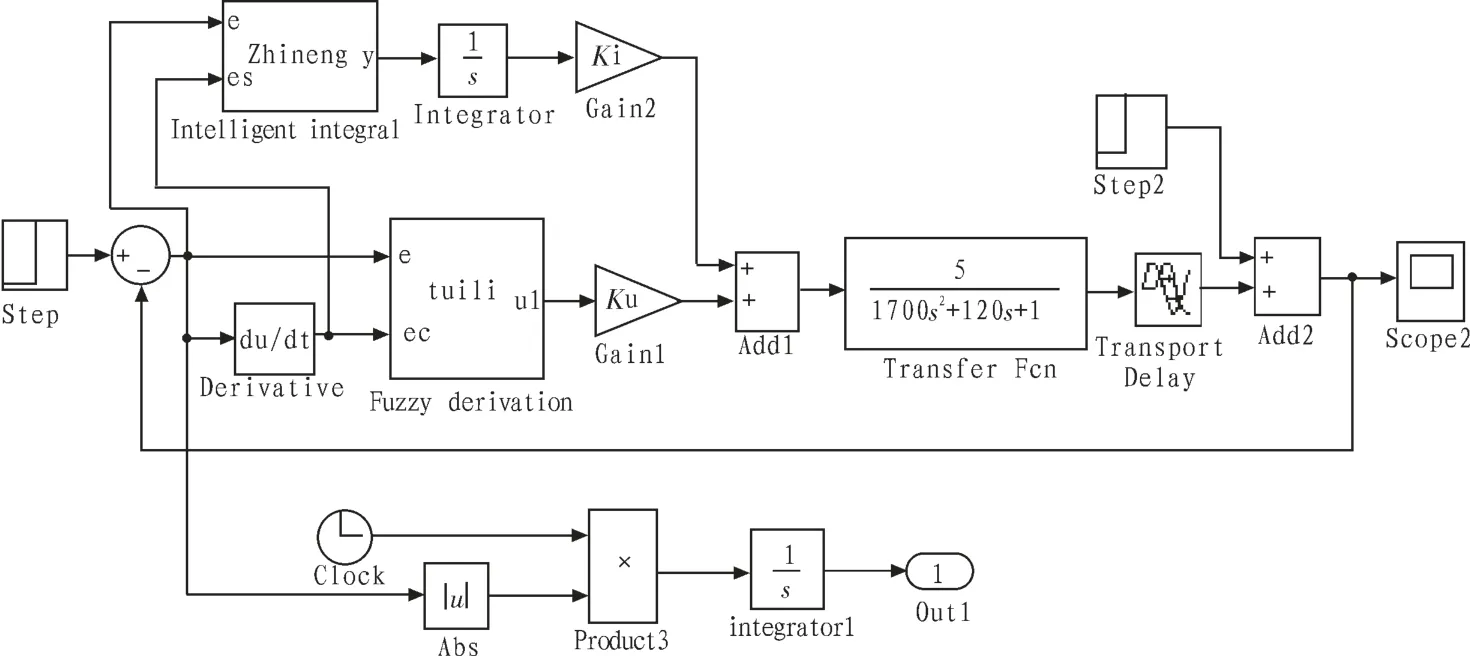
图2 模糊控制器仿真图Fig.2 Simulation diagram of fuzzy controller

经寻优可得初始化的参数K u＝1.570 9，K i＝0.009 3，α0＝0.439 3，αs＝0.781 0，将这些参数代入控制器仿真模块可得控制曲线。为了观察对比，同时对常规PID控制、未参数寻优的模糊控制器、经参数寻优的模糊控制器进行仿真，曲线对比如图3所示。由图可知设计出的模糊控制器在超调量和稳定性方面比常规PID控制有了比较明显的改进，当有扰动时，设计出的模糊控制器能更快的恢复稳定；对比参数寻优前后可知，经参数优化后模糊控制器在超调量上更小，在快速性方面更迅速，经扰动后能更快恢复稳定。

图3 仿真结果曲线对比图Fig.3 Results of simulation curve

3 液位控制实验结果

实验装置采用华晟公司的过程试验系统A3000，在这套装置中，下水箱和中水箱组成的双容器构成典型的双容液位系统。控制输入为中水箱的进水流量Qi，通过调节电动调节阀的开度控制中水箱的进水流量，中水箱的水经底部的水槽流入下水箱，控制对象为下水箱的液位高度H。将设计的模糊控制算法移植到西门子S7－200中，通过上位机组态王软件可以实时监控液位高度。

首先辨识控制对象的模型，突然加大调节阀开度观察液位随时间的变化，用飞升曲线法辨识可以得到液位控制系统的模型为：将 辨 识 出 得 数 学 模 型代入仿真可得控制器的初始化参数。算法移植到PLC中要注意误差和误差的变化率的求取，进入中断后采样值与目标值的偏差可以得到误差，比较上次误差与本次误差的偏差可以得到误差偏差率，算法求取的值为阀门的开度信号，经D/A转换为模拟量控制电动调节阀的阀门开度，在组态王的趋势图中可以记录观察实际的控制效果，实际监控效果如图4、图5所示。

图4 改进模糊控制器控制效果Fig.4 Control effect of improved fuzzy contoller

图5 PID控制器控制效果Fig.5 Control effect of PID contoller

当前设定的液位高度为30 cm，待系统稳定后加水使液位突变到33 cm，由两图对比看出，改进的模糊控制比传统PID控制的调节时间短，液位波动范围较小，有干扰信号时恢复到稳态的时间较短，整体控制性能要好于传统PID控制器。

4 结 论

设计了一种改进的带修正因子模糊控制器，并对该控制器进行了仿真验证，结果表明该控制器的控制效果相比传统PID有了改良，受到干扰也能较快的克服。将该控制器移植到PLC对水箱液位进行控制，实验表明该控制器的控制更哪快更平稳，为其他工业过程控制提供了新的思路。

[1]葛新成，胡永霞.模糊控制的现状与发展概述[J].现代防御技术，2008，36（3）：51－56.GE Xin-cheng，HU yong-xia.Present analysis and development trends of fuzzy control techniques[J].Modern Defence Technology，2008，36（3）：51－56.

[2]龙升照，汪培庄.Fuzzy控制规则的自调整问题[J].模糊数学，1982，（3）：105－111.LONG Sheng-zhao，WANG Pei-zhuang.Self-adjustment of fuzzy control rules[J].Fuzzy Mathematics，1982（3）：105－111.

[3]杨世勇.模糊与积分混合控制研究[J].自动化与仪表，2001，16（6）.YANG Shi-yong.Research on Hybrid control of fuzzy and integral[J].Automation and Instrumentation，2001，16（6）：65－70.

[4]高宏岩，王建辉.在线自调整修正因子模糊控制方法和应用[J].微计算机信息，2006（5）：83－85.GAO Hong-yan，WANG Jian-hui.A fuzzy control method with online self-turning correction factor and its application[J].Control&Automation，2006（5）：83－85.

[5]张岳峰.多修正因子的自适应模糊控制研究与实践[D].南京：东南大学，2008.

[6]张磊.基于单纯形法的PID控制器的最优设计[J].信息与控制，2004（3）：66－70.ZHANG Lei.Simplex method based optimal design of PID controller[J].Information and Control，2004（3）：66－70.