一种基于证据理论的可靠性信息融合方法
鲁 靖,卞树檀
(第二炮兵工程大学101教研室,陕西 西安 710025)
现代高技术兵器系统复杂,试验代价昂贵且周期太长,以及技术条件等方面的原因,系统级的试验越来越少,导致复杂系统现场试验数据很少。因此,以数理统计大样本理论为基础的可靠性评定方法已经不能适应现代武器系统的可靠性评定。Bayes方法[2]可以充分利用各种验前信息辅助可靠性评定。工程实际中普遍存在的仿真数据、历史试验、专家经验、子系统试验等同总体、同环境下的多源验前信息[1],此类信息在产品的设计、研制、生产、使用等各个环节都较为容易获取。而单一的验前信息对于装备可靠性试验评定来说,置信度较低,只有由多个单一验前分布融合得到一个合理的综合验前分布,才能提高评定的精度和可信度。上述同一状态产品多源信息的融合为加权融合问题,融合的关键是要确定不同验前分布在融验前分布中的合理的权重
目前,研究加权融合问题方法有很多:专家设定融合权重[3]、最大熵准则融合方法[2]、采用Bayes相继律融合法[4]、基于可信度的多源验前信息融合法[5]、相关函数方法[1]、模糊逻辑算子方法[1]、最大熵-矩估计方法[1]和充分性测度方法[1]等等。这些方法各具优势和适用范围。可信度融合方法较为合理,但可信度的计算比较困难。最大熵方法随着验前信息的增多,推导出来的验前分布的形式愈加复杂,会给验后分布的求取及Bayes推断造成一些计算困难,但是只要验前信息可信并且充分,得到的验前分布将会非常逼近实际的验前分布。而专家设定权重的方法虽然简便易操作,但却具有难以克服的主观随意性。
文中在简单介绍D-S证据理论的基础上,深入研究了加权融合的基本方法,将验前信息πi(θ)的融合问题转化为验后信息πi(θ|X)的融合问题,在小子样情况下,充分利用了验前信息和现场有限的数据X,在不考虑验后信息质量和相关性的前提下,利用各单一验后信息概率分布之间的一致性程度,确定线性加权中各验后分布的权重因子,最后得到一个综合的验后分布形式π(θ|X),结合现场数据亦可求取验前分布的综合形式π(θ),为同一状态产品多源信息融合提供新的思路。
1 D-S证据理论基础
D-S证据理论是用来处理由认识的局限性所带来的不确定性问题的有力工具。D-S证据理论是由Shafer[10]在1976年正式创立的。近年来,D-S证据理论在理论上得到了很大发展,在人工智能、决策、专家系统等领域得到了初步应用[7-8],另一面,D-S证据理论已经成功地应用在故障诊断、状态监测、信息融合、模式识别、智能决策等领域[9]。
D-S证据理的基本概念介绍:
对于一个判决问题,假设所有的可能结果用集合Θ表示,那么任何命题都将是集合Θ的一个子集,称Θ为识别框架[7,12]。

2 加权融合的一般描述

3 基于证据理论的验后分布计算
用Bayes法进行可靠性推断时,由先验数据x(i)1,x(i)
2,…,x(i)n,i=1,…,m,求得先验分布后πi(θ),结合现场样本X=(x1,…,xn),可得到θ的后验分布π(θ|X),即
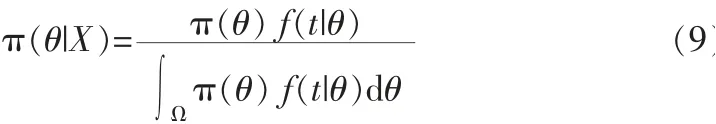
其中,Ω为参数θ的取值空间;f(t|θ)为可靠性指标随机变量T(如系统寿命)的概率密度函数;θ为待估计的分布参数。
假设事先知道θ的两组先验信息,通过先验信息获取的先验分布为π1(θ)和π2(θ),结合现场样本X=(x1,…,xn)得到π1(θ|X)和π2(θ|X)如图1所示。
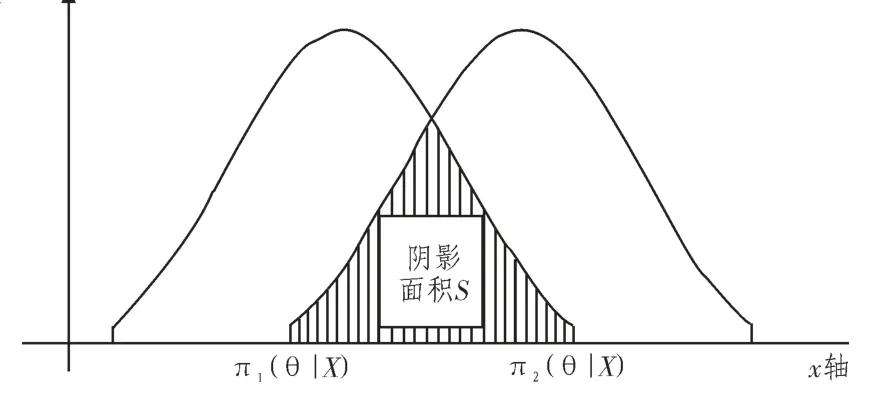
图1 有交集的两个概率分布Fig.1 Distributions of two probability with intersection


4 仿真实例

5 结 论
从信息论的角度来看,这种基于D-S证据理论融合方法合理充分地利用了产品同一状态的多源验前信息,融合得到的验后分布π(θ|X)增强了统计推断结论的稳健性,可以有效地减少试验的次数,从而减少了试验费用。从仿真实例计算说明,该方法简单易行,结果的精度和可信度是值得信赖的,在工程实践中有良好的前景和推广价值。
从上述仿真实例来看,得到结果π(θ)=N(4.9501,1)与仿真时采样分布N(5,1)非常接近。而从验后分布πi(θ|X)权重来看,π1(θ|X)与π2(θ|X)、π3(θ|X)一致度计算都较大,分别为0.5382和0.4769,由证据规则计算得到的权重γ1=0.5也较大,说明本文针对产品同一状态信息融合问题提出的方法是合理而有效的。融合得到验后分布π(θ|X)后,通过贝叶斯分析理论,进而以验后分布密度函数为基础进行点估计、区间估计、假设检验等统计推断。
[1]冯静.小子样复杂系统可靠性信息融合方法与应用研究[D].长沙:国防科学技术大学,2004.
[2]张金槐,唐雪梅.Bayes方法[M].2版.长沙:国防科技大学出版社,1992.
[3]Lesley W,John Q.Building prior distributions to support Baysian reliability growth modeling using expert judgement[J].Reliability Engineering and System Safety,2001(74):117-128.
[4]Xie M,Hong G Y,Wohlin C.Software reliability prediction incorporating information from a similar project[J].The Journal of System and Software,1999(49):43-48.
[5]张金槐.多种验前信息源情况下的融合验后分布[J].飞行器测控技术,1998,17(3):28-35.ZHANG Jin-kui.A variety of prior information source case fusion posterior distribution[J].Spacecraft TT&C Technology,1988,17(3):28-35.
[6]Shafer G.A mathematical theory of evidence[M].Princo-ton University Press,1976.
[7]段新生.证据理论与决策、人工智能[M].北京:中国人民大学出版社,1993.
[8]何友,王国宏,陆大绍,等.多传感器信息融合及应用[M].北京:电子工业出版社,2000.
[9]耿俊豹,邱玮,孔祥纯,等.基于粗糙集和D-S证据理论的设备技术状态评估[J].系统工程与电子技术,2008,30(1):27.GENG Jun-bao,QIU Wei,KONG Xiang-Chun,et al.Technical condition evaluation for devices based on rough set theory and D-S evidence theory[J].Systems Engineering and Electronics,2008,30(1):27.
[10]Shafer G.A Mathematical theory of evidence[M].Princeton:Princeton University Press,1976.
[11]杨军,武小悦,马溧梅.可靠性试验评定中专家信息融合[J].航空计算技术,2007.YANG Jun,WU Xiao-yue,MA Li-mei.Reliability test evaluation expert information fusion[J]. Aeronautical Computing Technique,2007,37(5):14-17.
[12]杨风暴,王肖霞.D-S证据理论的冲突证据合成方法[M].北京:国防工业出版社,2010.

