基于协同神经网络的导弹攻击目标识别方法研究

郭 巍，张千宇，王光辉

（海军航空工程学院 指挥系，山东 烟台 264001）

复杂背景下军事目标（飞机、军舰、坦克等）的自动识别，不要求其输出结果是一幅完整的图像本身，而是将图像经过某些处理后，再进行图像分割和特征提取，从而进行解决分类。这类问题属于模式识别的范畴，常采用经典的模式识别方法，主要是统计模式分类和句法（结构）模式分类。近年来新发展起来的模糊模式识别和人工神经网络模式分类在图像识别中也越来越受到重视。

二十世纪八十年代末，德国著名数学家、理论物理学家赫尔曼·哈肯（Herman Haken）教授提出了模式识别的新概念——协同模式识别（Synergetic Pattern Recognition，SPR）[1-2]，从自上而下的角度出发，描述了协同模式识别基本方程的构造原理，并提出了一个重要的观点：模式识别的过程即为模式形成的过程。

协同模式识别从整体上分析目标的特征，识别过程符合人类的感知机制，以哈肯教授为核心的研究小组将协同模式识别用于2D工业零件识别[3]、手写体字符识别、3D图像校正和立体视觉中的视差计算等，取得了一些实践结果，另外一些研究人员试图解决图像分割问题或构造基于协同学原理的联想记忆模型。德国斯图加特大学的Banzhaf教授等人对协同竞争学习机制作了深刻的研究[4]。

在国内，也有不少学者对协同模式识别进行了大量的研究，上海交通大学从1977年起，对协同理论进行了多方面深入而有意义的研究工作[5]。而合肥工业大学也从2000年开始，对协同模式识别等内容进行了从理论方法到实际应用各方面较为深入的研究工作[6]。另外北京师范大学、重庆大学等高校也先后不同程度的对协同理论方法与应用进行了研究[7-8]。

1 目标识别协同神经网络的实现

1.1 协同神经网络的构成

文献[1]给出了用于协同识别的动力学模型，我们可以用一种并行的神经网络算法进行求解：

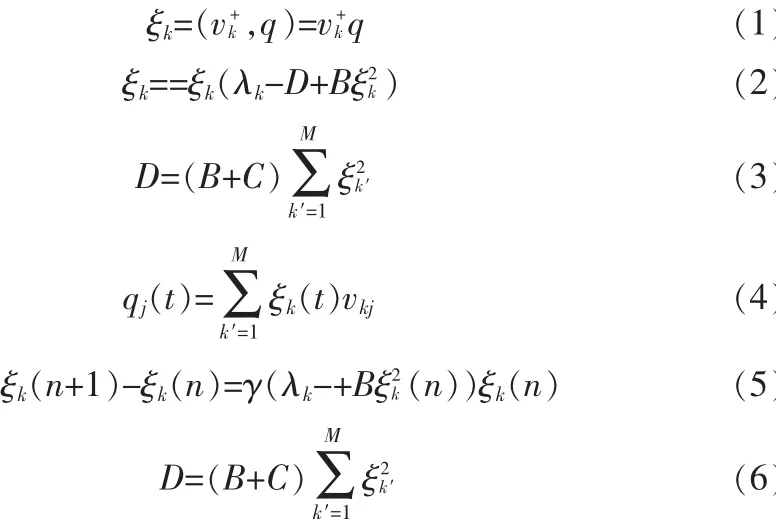
式（5）中，γ为迭代步长，离散协同神经网络的稳定性将主要取决于γ的大小。于是，Haken网络可以转化为图1所示的类似三层前向网络的形式，只是中间层序参量按式5动力学方程进行演化。

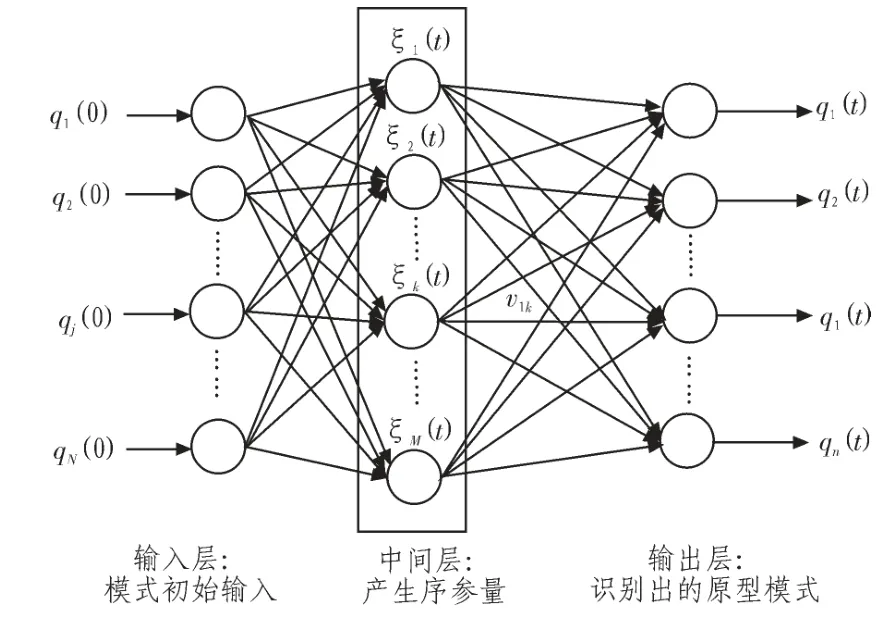
图1 协同神经网络的结构Fig.1 Structure of the synergetic neural network

1.2 协同神经网络的运行步骤

协同神经网络的运行过程包括两个阶段：首先是网络的学习训练阶段，然后是网络的识别阶段。具体运行步骤如图2所示。

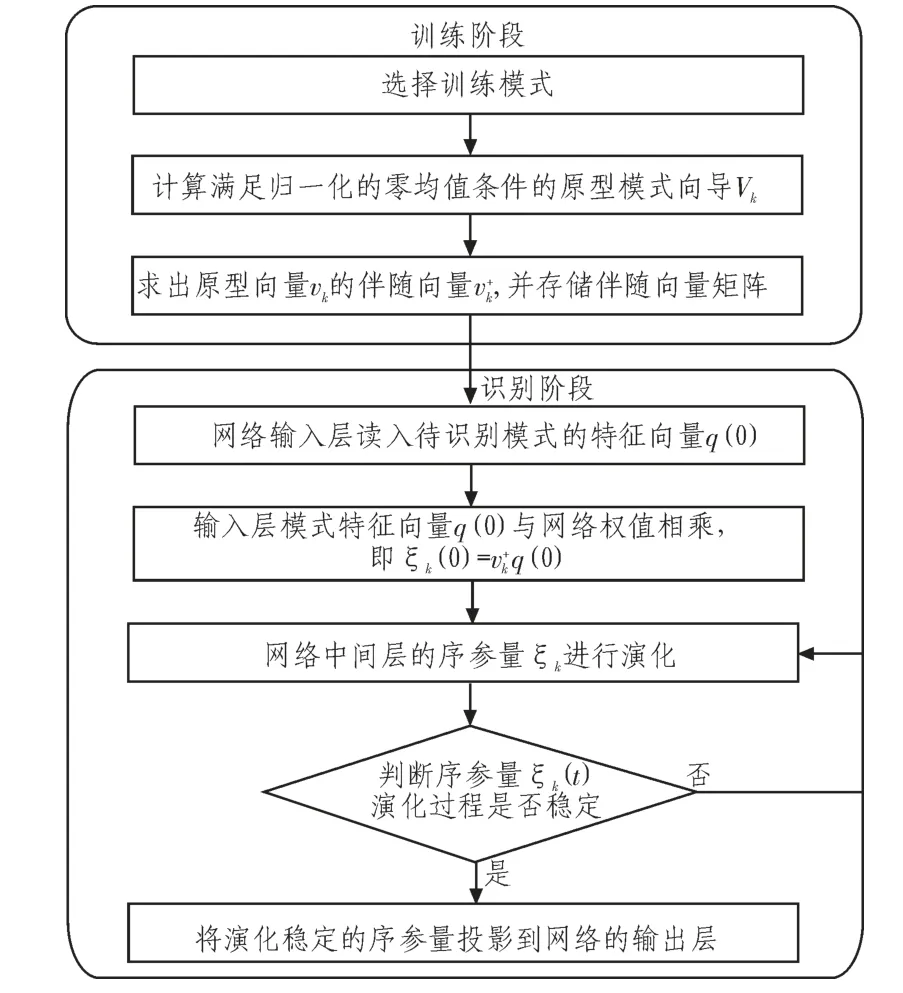
图2 协同神经网络具体运行步骤Fig.2 Process of the synergetic neural network

1.3 协同神经网络稳定性分析

文献[2][8]分别从权矩阵特征值非负及势函数的稳定最小点等方面详细讨论了连续协同神经网络具有全局稳定性，这里不再赘述。离散协同网络的稳定性与该网络的迭代步长有很大关系。步长过大，会导致各个序参量的变化过于剧烈，而偏离原来的稳定轨道，使网络呈发散状态，导致系统无法完成识别功能。

通常来说，只要步长取得足够小，就能保证系统收敛，但从下面的分析可以看出，序参量ξk的变化范围及几何分布情况随着原型模式与待识别模式的变化有很大差异，要想找到一个在任何情况下都能保证系统稳定收敛的固定步长将很困难，即便能够满足要求，其识别速度及效率也将大幅度降低。为了避免在训练过程中不至于出现太大的竞争波动，在这里对步长γ进行分析，以保证协同离散网络能够快速、稳定地收敛。

综上所述，为保证系统应对每一模式均收敛，当ξ2k（n）取最小值0时，亦应收敛，因此离散协同神经网络的迭代步长γ应满足：

2 仿真研究

综上所述，整个识别流程如图3所示。

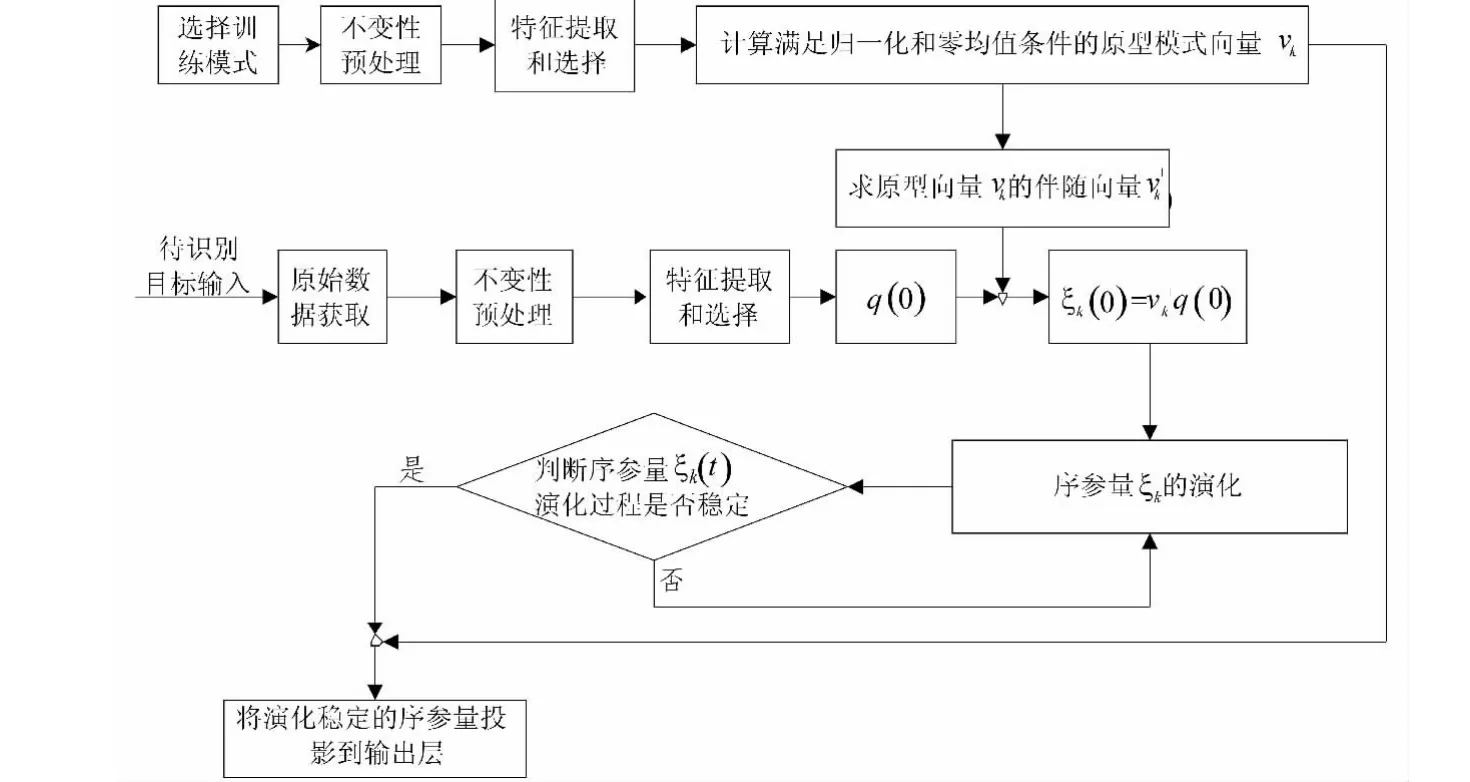
图3 目标识别流程图Fig.3 Flow chart of the target recognition

取10个飞机图像作为训练样本，图像大小为，每张图片可以用一个4 096维向量描述，这些向量就是训练样本的原型模式vk，这里一共有10个样本，训练样本的原型模式如图4所示。

图4 训练样本的原型模式Fig.4 Prototype pattern of the training sample

则原型模式分别对应的伴随模式v+k如图5所示。

图5 原型模式对应的伴随模式Fig.5 Adjoint model corresponging the prototype pattern

1）待识别样本只是在训练样本的基础上进行加噪，没有发生平移、旋转或者伸缩时，如图6所示。

图6 待识别图像Fig.6 Picture to be identified

我们不需要对其进行不变性处理，直接输入到协同神经网络中进行识别。按照稳定性分析方法，取时能够得到快速稳定的序参量收敛曲线，识别的形成过程如图7所示。

图7 识别的形成Fig.7 Target recognition's formation

此时的序参量及势函数演化为：

2）当待识别样本图像只是训练样本残缺的基础上进行 加噪，也没有发生平移、旋转或者伸缩变化，如图9所示。

图8 序参量及势函数演化曲线Fig.8 Evolution curve of the order parameter and potential function

图9 残缺的待识别模式Fig.9 Incomlete pattern to be recognized

我们不需要对其进行不变性处理，直接输入到协同神经网络中进行识别。同样取得到识别的形成如图10所示。

图10 待识别模式残缺时模式的形成Fig.10 Pattern s formation incomlete pattern to be recognized

此时的序参量及势函数演化曲线：

从而可以看出，协同神经网络对于残缺的待识别模式同样具有很好的有效性。

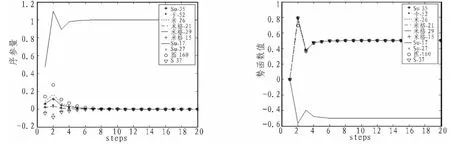
图11 待识别模式残缺时序参量及势函数演化曲线Fig.11 Evolution curve of the order parameter and potential function incomlete pattern to be recognized

3 结束语

文中论述了协同学理论在模式识别中的应用，介绍了基本的协同识别模型及其算法框架；介绍了协同神经网络并对其运行步骤和稳定性进行了分析；使用协同神经网络相结合对军事目标的识别进行了研究；最后并通过MATLAB对该方法在目标识别中的应用进行了仿真。

[1]Haken H.协同计算机和认知——神经网络的自上而下方法[M].杨家本，译.北京：清华大学出版社，1994.

[2]Daffershofer A，Haken H.Synergetic computers for pattern recongnition——A New Approach to Recognition of Deformed Patterns[J].Pattern Recognition，1994，27（12）：1697－1705.

[3]Wang F Y，Fever P J A，Pu B.A robotics vision system for object identification and manipulation using synergetic pattern recognition[J].Robot.Comput.Integrated Manufacturing，1993，10（6）：445－459.

[4]Banzhaf W，Schmutz M.Some Notes on Comperirion Among Cell Assemblies[J].Int’l Journal of Neural Systems，1992，2（4）：303－313.

[5]HU Dong-liang，QI Fei-hu，LIU Jian-feng.Recognition of objects with shew distortion based on synergetics[J].Pattern Recongnition Letters，1999（20）：255－265.

[6]Jun Gao，Jie Bao，Dingguo Chen.Optical-electrotronic Shape Recognition System Based on Synergetic Associative Memory.Proceedings of SPIE Applications of Artificial Neural Networks in Image ProcessingⅥ[C].San Jose，USA：Jan.2001，4305：138－148.

[7]吴渝.小波多分辨率分析模型研究与协同计算机[D].重庆：重庆大学，1997.

[8]郑南宁.计算机视觉与模式识别[M].北京：国防工业出版社，1998.