时频系统中主备钟一致性保持方法的研究

卢建福，高玉平，林思佳，刘彪



时频系统中主备钟一致性保持方法的研究

卢建福1,2，高玉平1,3，林思佳1,2，刘彪1,2

（1. 中国科学院国家授时中心，西安 710600；2. 中国科学院大学，北京 100039；3. 中国科学院时间频率基准重点实验室，西安 710600）

为保证主、备钟切换时时间信号的准确性和稳定性，开展了主、备钟一致性保持方法的研究。搭建了进行主、备钟一致性保持的实验系统，阐述了系统的原理，分析了不同钟差预测模型的效果，给出了计算备份钟频率补偿量的公式，测试了系统在不同控制周期下的同步水平。测试结果表明：采用本系统的主、备钟一致性保持方法，能够实现主、备钟间的最大时间偏差小于1ns的指标，同时提高了备份钟的长期频率稳定度。

原子钟；时间同步；频率驾驭

0 引言

随着我国国民经济、国防建设和空间技术的发展，对高精度时间频率服务的准确性、稳定性和可靠性提出了越来越高的要求。在实际应用中，时间和频率信号常被作为业务工作的参考基准，因此需要具有准确性、连续性、稳定性和可靠性等特点；通常，时间频率信号是由时频系统中的原子钟产生，为保证输出信号的连续性和可靠性，时频系统中建有备份原子钟，并需要对主、备钟输出的时频信号进行一致性保持。为此，搭建了主、备钟一致性保持的试验系统，实现了两个原子钟间实时相位同步，必要时进行工作钟与备份钟间信号的切换。

1 系统原理

1.1 主、备钟一致性保持的原理

图1所示是主、备钟一致性保持系统的原理框图。

图1 主、备钟一致性保持系统的原理图

工作钟采用中国科学院国家授时中心的铯钟（HP5071A型），该钟拥有较好的长期稳定性，但噪声较大；备份钟采用商品铷钟（FS725型），其噪声小，但存在频率漂移。系统正常工作时，工作钟的1PPS信号通过转换开关后作为时频系统的输出，同时，备份钟的10 MHz信号经过相位微调仪后输出的1PPS与工作钟的1PPS通过时间间隔计数器SR620进行钟差的测量，测量结果经过数据处理和控制模块的分析后，得出备份钟相对于工作钟的频率偏差和相位偏差，并根据和的值制订相应的频率调整策略，计算出给备份钟添加的频率补偿量，最后将补偿量反馈到相位微调仪中对备份钟进行频率驾驭，实现工作钟与备份钟之间的实时相位同步。当系统检测到工作钟信号异常时，时频系统的输出将切换到相位微调仪输出的1PPS上，保证了系统输出时间信号的连续性。

1.2 系统运行流程

图2给出了系统进行主备钟一致性保持的流程。首先，系统进行等间隔的钟差采集，当采集的点数达到某预设值时，采用3准则进行数据预处理实现粗差剔除；然后，求出此时备份钟相对于工作钟的频率偏差以及当前的预测钟差；最后，由与的值计算添加到备份钟的频率调整量，并通过相位微调仪HROG-10实现对备份钟的频率控制，整个过程称为一个测控周期（c），频率的测控在系统运行过程中是自动、连续、循环进行的。钟差预测和频率偏差计算的方法在第2节中介绍，频率补偿量的计算在第3节中讨论。

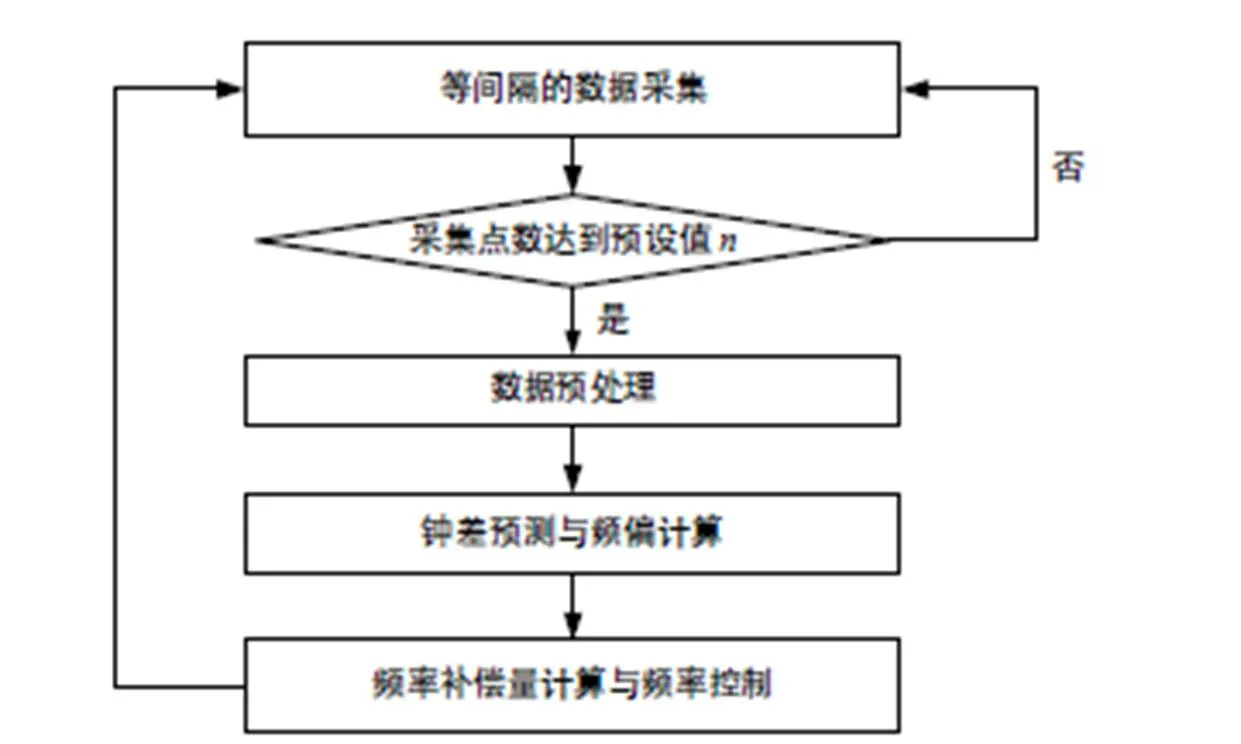
图2 主、备钟一致性保持的流程

2 钟差预测与频偏计算

系统采用时差法测量2个原子钟间的频率偏差。时差法是根据2台钟输出的1 PPS信号的时间差随时间的变化情况来确定两者间的频率偏差。在时刻，工作钟与备份钟的时差为，经过时间后，变为，则相对频率偏差的计算如式（1）所示：

在实际的数据处理中，由于噪声对测量结果的影响，不直接用测量值求频率偏差，需要对钟差进行预测。下面给出了3种钟差预测的模型：灰色模型，二阶多项式模型以及一阶多项式模型[1]，并给出了其对应频偏的计算公式。

1）灰色模型

灰色模型是用指数函数作为拟合函数对等间隔的钟差数据进行拟合，通过对原始钟差数据实行累加或累减使之成为具有较强规律的新数列，然后对此生成数列进行建模。设原始钟差数据列为

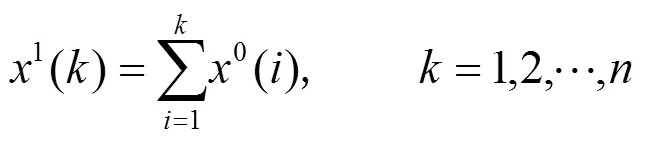
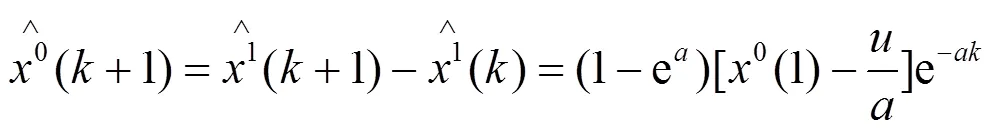
2）二阶多项式模型

3）一阶多项式模型

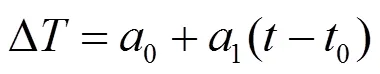
对上述3种模型下预测钟差与实测钟差的差异进行测试：每3 s采集1个数据，每100个点进行一次钟差预测，测试结果如图3所示。

图3 不同模型下的预测钟差值与实测钟差值之差

由图3可见，一阶多项式和二阶多项式模型下，钟差预测值与实测值之差均在0.3 ns以内，该差异是由原子钟自身噪声和系统测量误差引起的，该2种模型下钟差预测效果相当；灰色模型下，预测值与实测值之差达到1.5 ns，此差异不是简单地由噪声和测量误差引起，表明灰色模型不适合对同步系统进行钟差预测。与二阶模型相比较，一阶模型相对简单，且预测效果不逊于二阶模型，故本文选用一阶多项式模型进行钟差预测和相应频偏的计算。

3 频率补偿与效果分析

3.1 同步状态的划分

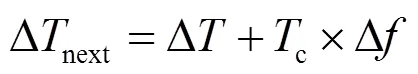
将也进行区间划分，图5是区间划分的示意图。

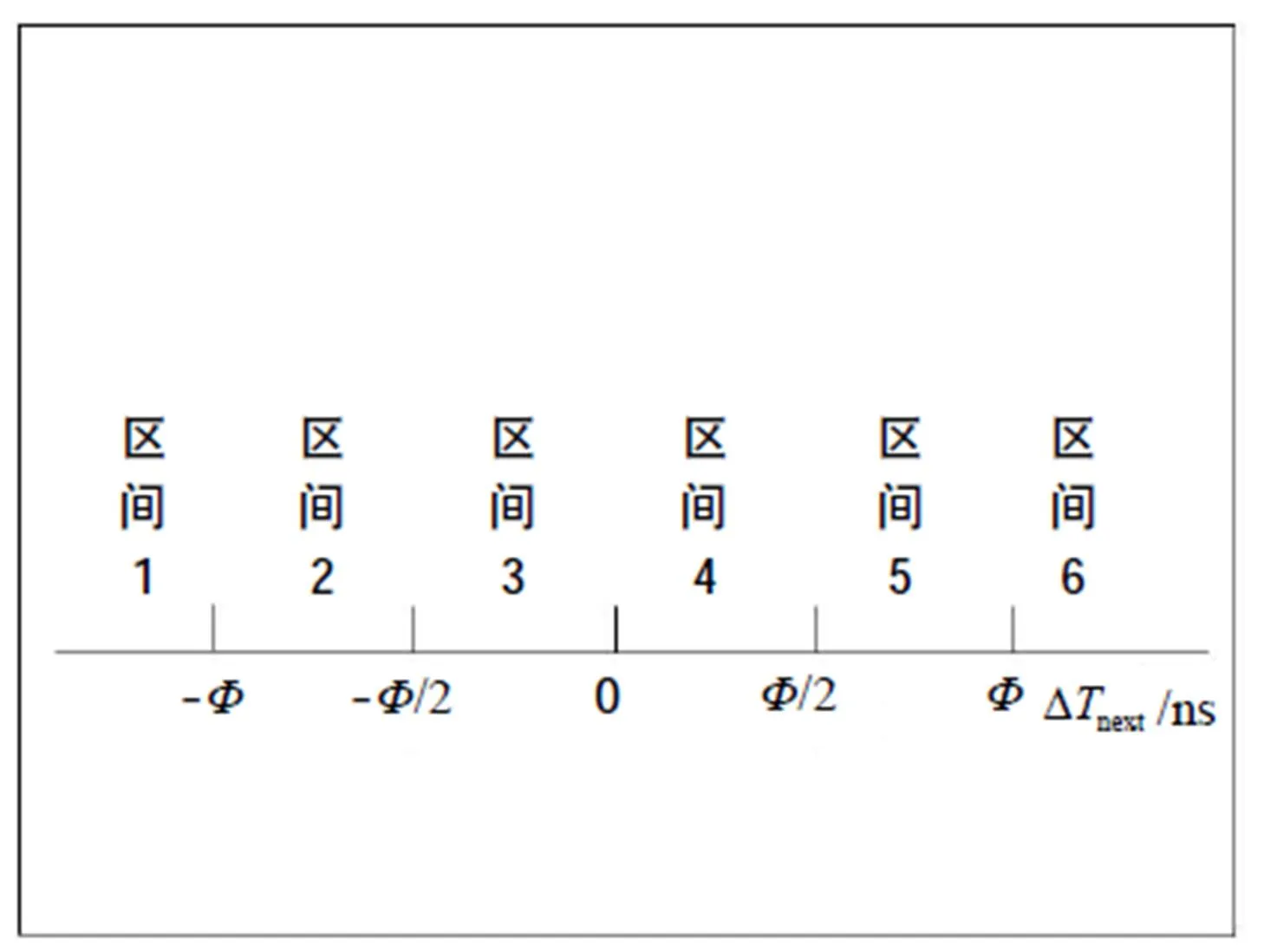
图5 区间划分示意图

3.2 频率补偿的方案

进行原子钟的频率补偿时需要考虑2个问题[2]：1）为了尽可能快地去除相位差而使补偿量太大，出现过度调整；2）为保持时间的稳定度，对补偿量加以限制，避免出现剧烈波动，而使相位差不能达到最小。系统进行频率补偿时遵循的原则是：保证相位同步精度的前提下，尽可能地提高备钟输出信号的频率稳定度，避免出现过度调整现象。下面以原子钟处于状态1和状态5时为例，介绍频率补偿的方案。

表1根据控制后对钟差数据的分析，列出了同步状态1时频率补偿量的计算公式，表2列出了同步状态5时频率补偿量的计算公式。

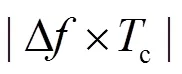
表1 状态1下频率补偿量的计算公式列表

注：表中表示上一个控制点处的频率补偿量。

表2 状态5下频率补偿量的计算公式列表

注：表中表示上一个控制点处的频率补偿量。

3.3 测试效果分析

图6 不同测控周期下钟差曲线图

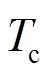
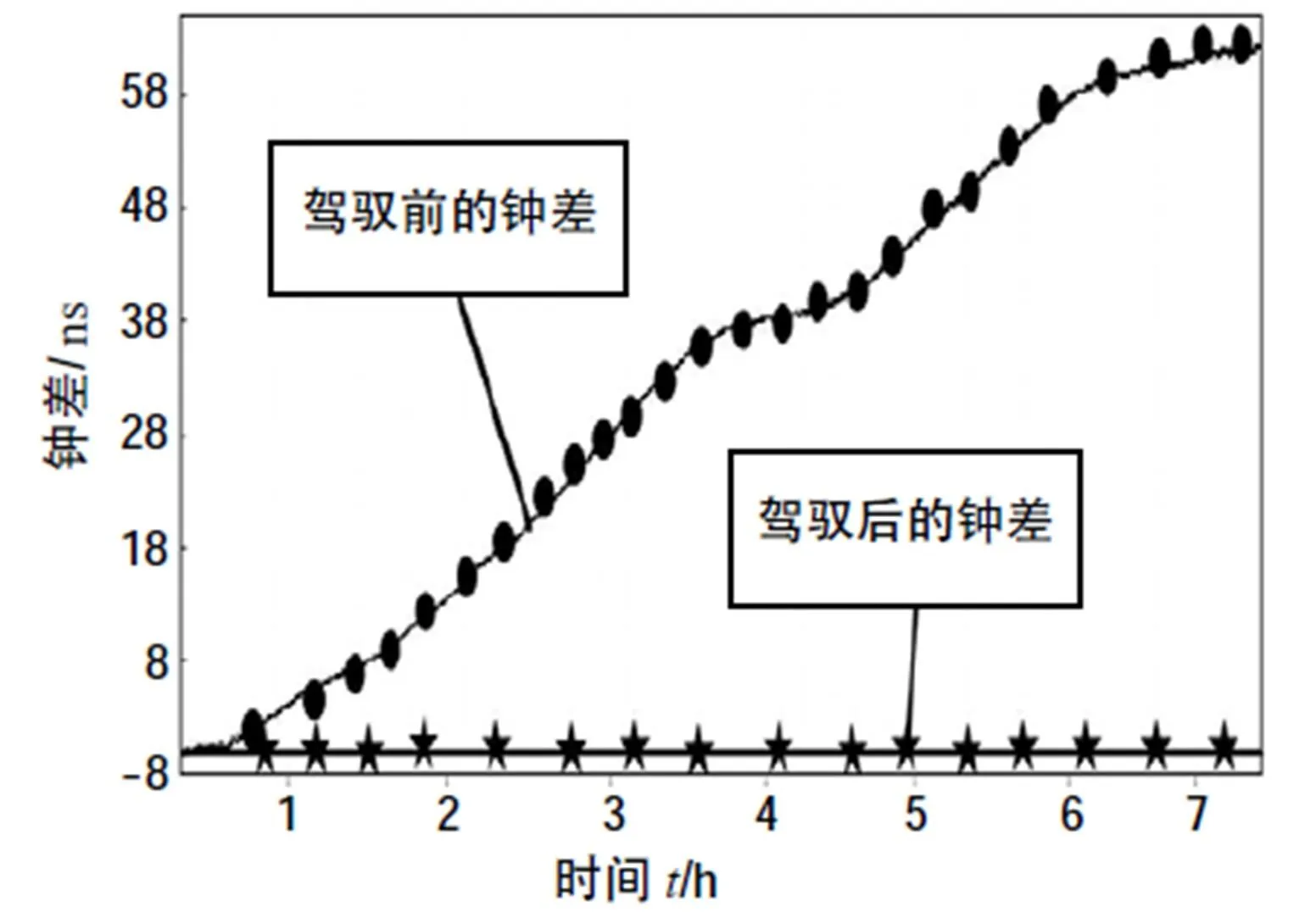
图7 驾驭前后钟差曲线（＝150 s）

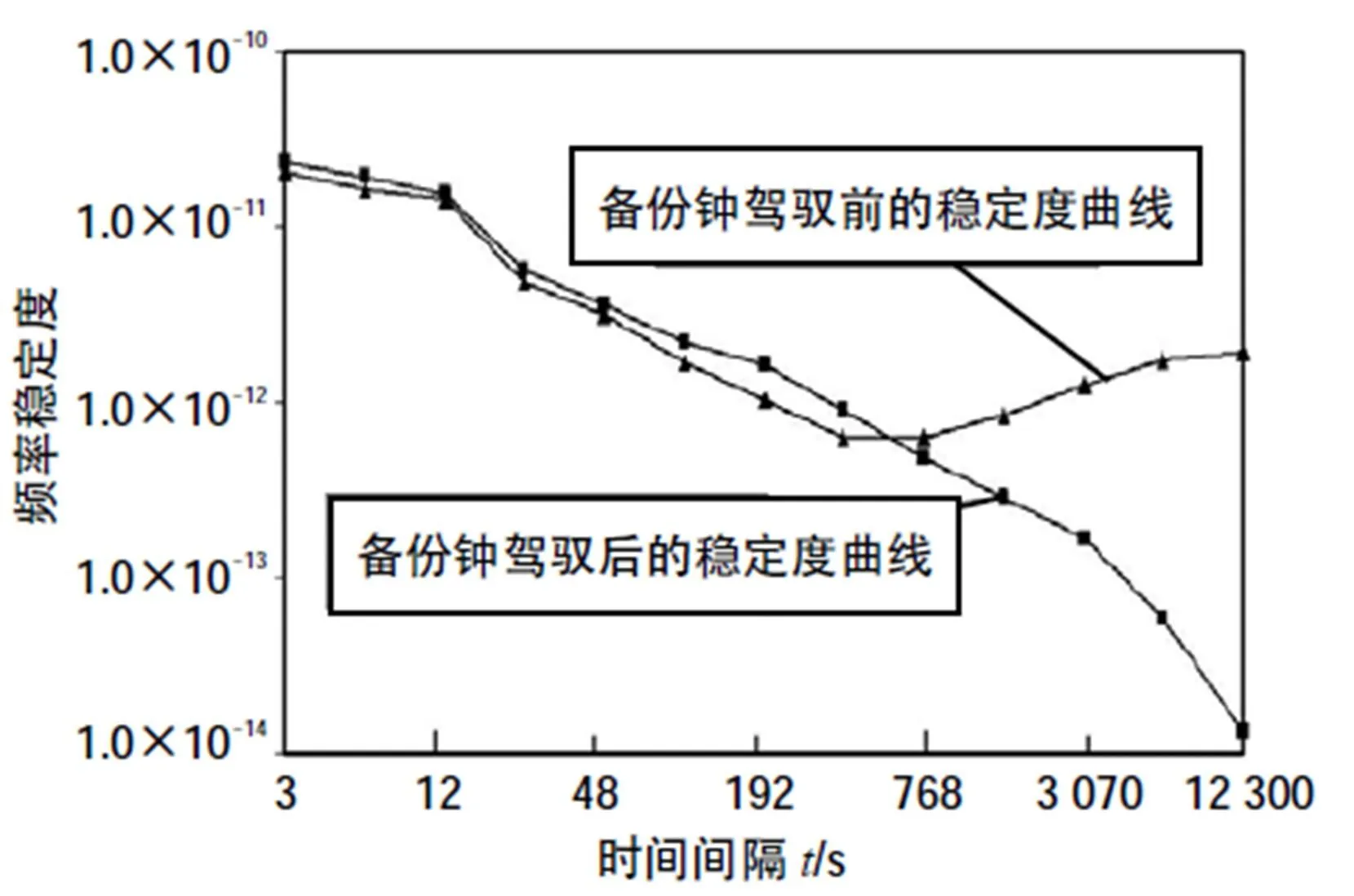
图8 驾驭前后的稳定度曲线（＝150 s）

4 结语

本文设计并实现了铯原子钟与铷原子钟间的相位一致性保持系统。通过测试分析表明：采用本文所述的主、备钟一致性保持方法，可以实现2个原子钟间相位实时偏差小于1 ns的要求，并能有效地提高备份钟输出信号的长期频率稳定度。对于不同的系统，测控周期的大小应先根据目标精度与备份钟的稳定度确定相应的范围，最后通过实际的测试效果确定测控周期的大小。

[1] 朱陵凤, 李超, 刘利, 等. 基于国产氢原子钟的钟差预报方法研究[J]. 大地测量与地球动力学, 2009, 29(1): 148-151.

[2] 李变. 机动条件下时间保持方法研究[D]. 北京: 中国科学院研究生院, 2011.

[3] 邢彦超, 杨俊, 汤超, 等. 一种铷原子钟双钟热备相位无扰切换系统的设计[J]. 时间频率学报, 2011, 34(2): 101-106.

[4] 王正明, 袁海波. 氢钟和铯钟联合守时初探[J]. 天文学报, 2007, 48(1): 72-83.

Study of methods of maintaining consistency between primary and backup clock in time/frequency system

LU Jian-fu1,2, GAO Yu-ping1,3, LIN Si-jia1,2, LIU Biao1,2

(1. National Time Service Centre, Chinese Academy of Sciences, Xi′an 710600, China;2. University of Chinese Academy of Sciences, Beijing 100039, China;3. Key Laboratory of Time and Frequency Primary Standards, National Time Service Center,Chinese Academy of Sciences, Xi′an 710600, China)

In order to ensure the accuracy and stability of time signal in switching the primary and backup clock, we studied the methods of maintaining consistency between the primary and backup clock and built an experiment system to maintain the consistency between the primary and backup clock. In this paper, the principle of the system is demonstrated, the results of different clock offset prediction models are analyzed, and the formula of frequency compensation for backup clock is given. The levels of synchronization for different control cycles are tested and the tests show that by using the method described here the time difference between the primary and backup clock is less than 1ns as well as the long-term frequency stability of the output signal of the backup clock can be improved.

atomic clock; time synchronization; frequency steering

TM935.115

A

1674-0637(2013)04-0222-07

2013-01-22

国家自然科学基金资助项目（11103025）

卢建福，男，硕士，主要从事时间同步方法研究。