卸荷下老黏土的静力特性试验研究

陈 聪，郑新定，刘召刚，简琦薇，周 健，陶文涛，侯云亮

(1.武汉地铁集团有限公司，湖北 武汉 430070;2.中铁隧道勘测设计院有限公司，天津 300133;3.同济大学，上海 200331)

0 引言

作为一种区域性黏性土，老黏土具有特殊的工程性质，多年来一直受到工程界的关注。近年来，对老黏土的研究比较多［1－5］，但是现有的一些研究成果是在常规土工试验基础上取得的，尚不能很全面、系统地反映老黏土的工程性质，特别是土体在卸荷状态下的工程性质。

土体的强度和变形参数受应力路径的影响变化很大。当前大多数本构模型对土工参数的取用是在加载试验基础上取得的，对基坑开挖及隧道这类卸荷工程不甚适用。因此，对这类工程有必要区别于加载试验，按工程的实际情况采用卸荷下的三轴试验指标。朱百里等［6］用粉质黏土进行了不同K0固结的等K应力路径试验，并确定了修正剑桥模型参数，将其用于深基坑开挖分析。陈永福等［7］对上海灰色黏土进行了卸荷－再加荷三轴试验，提出估算基坑回弹量和全补偿沉降的计算式，建立了相应的应力－应变模型。张文慧等［8］通过各项等压轴向加载三轴压缩试验和等应力比固结侧向卸荷三轴试验研究了应力路径对基坑工程变形的影响。本文在三轴试验结果的基础上，首先对卸荷下武汉老黏土的应力应变关系进行归一化处理，并推导了老黏土应力应变的关系式，为其本构模型的建立和参数选取打下基础。

1 试验方案

1.1 试验土样

试验土样取自武汉钟家村地铁项目，为粉质黏土，呈硬塑状态，局部夹碎石。老黏土局部(呈鸡窝状分布)存在弱膨胀潜势，虽强度较高，但遇水易软化，易产生边坡失稳。其物理性质指标见表1。

1.2 试验排水条件

为了模拟施工过程中开挖、降水等实际情况，真实反映坑底及坑周土体应力路径的改变，本次三轴应力路径试验采用固结不排水条件。

表1 老黏土的物理性质指标Table 1 Physical indices of old clay

1.3 试验参数选取

基坑开挖是在土的原始状态下完成的，因此，卸荷试验前应首先恢复土体原有的应力状态，选用K0固结。K0取 0.65，固结围压取 100，200，400 kPa。

围压卸荷比 η =Δσ3/σ3，取 10%，30%，50%。应力变化比 δ=Δσ1/Δσ3，取0，0.5，2。

对于黏性土，固结稳定的标准为1 h内固结排水量变化小于0.1 cm3，或5 min内轴向变形不大于0.005 mm。结合武汉老黏土的实际工程性质，本试验固结时间统一为12 h。

对于按应变控制的不排水剪切试验，黏土应变宜为(0.05% ～0.10%)/min。本试验应变为 0.08%/min，达到20%的应变需4 h左右。

对于脆性破坏的试样，将会出现峰值，则以峰值作为破坏点，如果试样为塑性破坏，则按应变量的15%作为破坏点。

2 试验结果分析

2.1 试验破坏的主要型式

老黏土三轴试验过程中，试样剪切破坏面是逐渐发展的。如图1所示有一部分土体基本上呈鼓状破坏，并出现一定的径向变形;另外一部分剪切破坏面比较明显，并与最大主应力约呈(45°+φ/2);认真观察各剪切带在三轴试样中出现的位置和延伸方向，可以发现武汉老黏土三轴剪切带滑裂面出口通常可以延伸到试样端部透水石位置，这种破坏型式跟老黏土的结构特征有关。

图1 试样破坏型式Fig.1 Failure situations of specimens

2.2 应力应变特性曲线

根据卸荷下的三轴试验结果，将各组试验所得数据经过整理，以轴向应变εa为横坐标，以主应力差(σ1－σ3)为纵坐标绘制偏应力－轴向应变关系曲线，如图2所示。

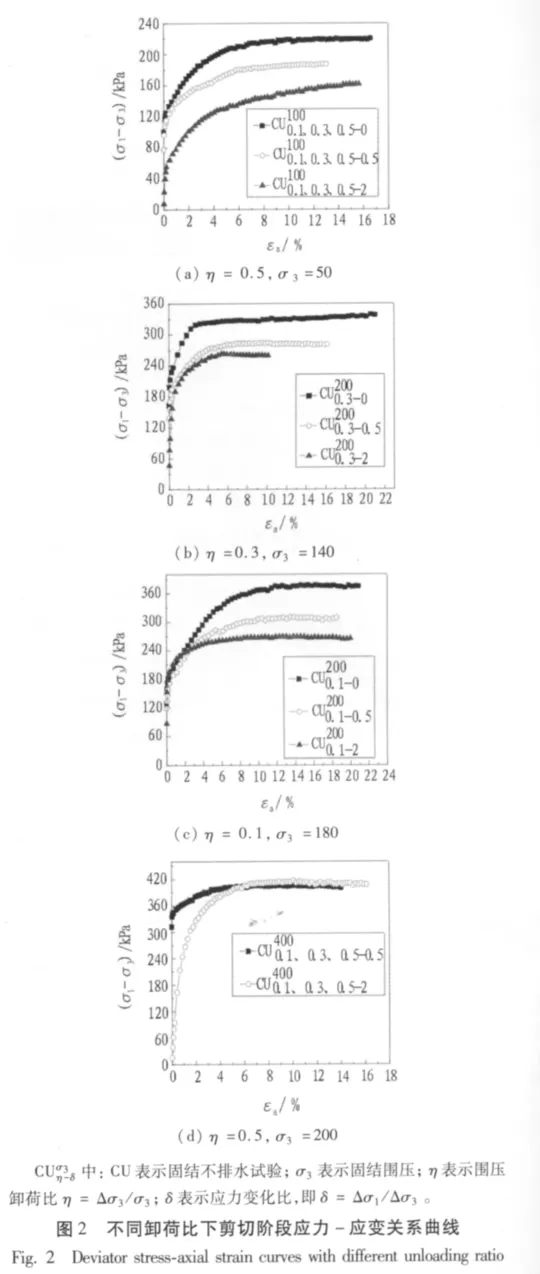
通过上述不同卸荷比与应力变化比下的几组常规三轴试验曲线可知，老黏土的应力－应变特性如下。

1)应力－应变曲线近似为双曲线型，多为硬化型曲线，说明土体经过弹性变形及塑性屈服阶段后并没有进入明显的破坏阶段，即没有明显的峰值破坏点。土体在塑性变形屈服后强度继续增长至相对稳定，在剪切过程中结构变得紧密，表现为剪缩，因而强度也在提高，呈现硬化特性。但也有部分试样试验曲线表现为一定的弱软化性，这主要与老黏土的结构性有关，原状土取不同的土层，其性质有较大的差别。

2)偏压固结(K0固结)下，剪应力在固结过程已经存在，从而造成在剪切阶段的变形特性与等压固结不同，土体达到屈服后较小的应力增量下会产生较大的轴向变形，应力－应变关系基本上为水平直线状，即表现为理想的弹塑性材料的变形性质。

3)在卸荷的情况下，土体的应力应变曲线有明显的区别，主要表现为土样在应变较小时呈现明显线性，这是因为土体在经历卸荷时发生回弹变形，再压缩时将会有比较大的弹性变形;在弹性变形后，经历过卸荷路径的土体应力增长有限，应变发展较快，塑性变形明显，特别是当卸荷量较大时，在围压较大的情况下，应力－应变曲线基本呈理想塑性变形状态。

4)由图2(d)可知:土样在卸荷过程中只要不拉断，在再加载过程中总有一定的强度，特别是伸长应变小于1%时，抗剪强度并没发生多大变化;当伸长应变大于1%时，由于土体结构被破坏，再加载时的抗剪强度会大大低于无卸载时的强度。

不同卸荷比下老黏土的基本变形特性为:武汉老黏土表现为非线性特性，但卸荷下也具有比较明显的线性阶段特性;剪切过程具有硬化特性和剪缩性，部分土样具有一定的弱软化性。

2.3 老黏土与软土土样的对比分析

为了对武汉老黏土的变形特性有更加清晰地认识，本文特选择武汉软土土样进行对比分析。

张勇［9］基于武汉软土的固结不排水三轴剪切试验，分析了武汉软土的应力－应变关系特性:在低围压下，土体表现出稳定型或弱应变硬化型;在高围压下，土体呈现出弱应变软化型;土体的应力－应变关系曲线为典型的双曲线;并用主应力差渐近值作为标准归一化因子，从理论上推导了应力－应变归一化方程。

通过对比分析，老黏土不同卸荷比下的偏应力随轴向应变的增加而增大，偏应力－轴向应变曲线基本相似，呈应变硬化状态，这可能与老黏土的结构性有关。

2.4 应力应变归一化特性研究

分别采用围压σ3和平均固结压力σm进行应力应变特性归一化分析，如图3所示。从图3可以看出，老黏土在偏压固结下三轴试验应力应变曲线具有归一化性状，但还存在一定的离散性。造成归一化离散性的原因主要是原状土样的非均匀性和土样的扰动，还有每次试验操作所存在的不可避免的误差;固结状态的不同也对归一化性状有很大的影响，一般土体在正常固结状态归一化性状较好，超过一定的固结压力，土体的归一化性状会差些。图4为采用εaσ3/(σ1－σ3)～εa和 εaσm/(σ1－ σ3)～ εa进行归一化曲线。

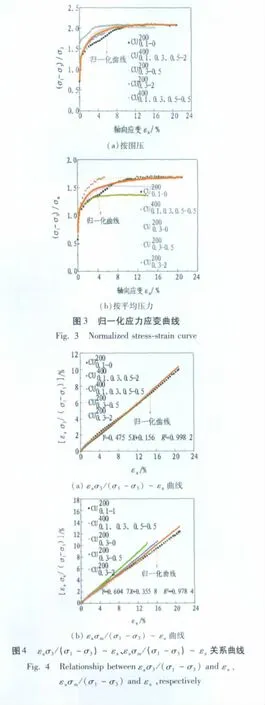
1)采用围压进行归一化。图4(a)为采用围压归一化应力应变关系曲线来表示土体的应力应变关系。从图中可以看出二者基本上成线性关系，表达式如下:

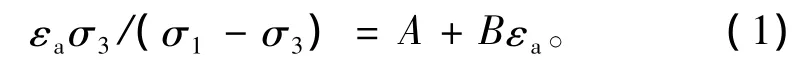
2)采用平均固结压力进行归一化。图4(b)为采用平均固结压力εaσm/(σ1－σ3)归一化应力应变关系曲线来表示土体的应力应变关系。从图中可以看出这二者也基本上成线性关系，表达式如下:

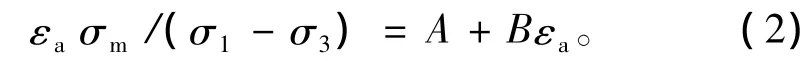
式(1)和式(2)都具有典型双曲线形状，都能反映老黏土固结不排水试验的归一化应力应变特性，其中参数A和B均表示试验归一化应力应变关系曲线的相关参数，反映了土体在相应状态下的变形特征和强度特征，其取值如表2所示。

表2 老黏土三轴试验归一化应力应变曲线参数Table 2 Parameters of normalized stress-strain curve of old clay on tri-axial test

归一化曲线可以用来确定相同试验条件下其他应力状态下土体的性状。图3为不同固结压力下，饱和老黏土的不排水(σ1－σ3)/p'和轴向应变εa的归一化曲线。由于试样的不均匀性及试验步骤上的某些差别，曲线有些差异。对于相同剪切方式，不同初始固结应力的土体其归一化强度基本一致，对于不同剪切方式的土体归一化强度会有所差异。

2.5 老黏土的Duncan－Chang模型及参数确定

2.5.1 Duncan－Chang模型

Duncan－Chang模型是基于弹性理论的非线性弹性模型，采用Kondner双曲线公式来推导关于土体本构关系的双曲线模型。

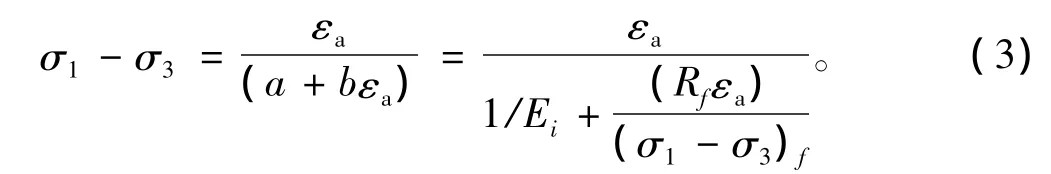
式中:初始切线模量Ei=1/a;(σ1－σ3)f表示土样破坏时的偏差应力(即强度);(σ1－σ3)ult表示双曲线的渐近线所对应的偏差应力，(σ1－σ3)ult=1/b;破坏比 Rf=(σ1－ σ3)f/(σ1－ σ3)ult=b(σ1－ σ3)f，Rf一般为 0.75 ～ 1.00。

2.5.2 参数确定

1)c，φ值确定。由表3绘制不同围压下的摩尔应力圆，见图5。

c=51.6 kPa，φ =23.1°。

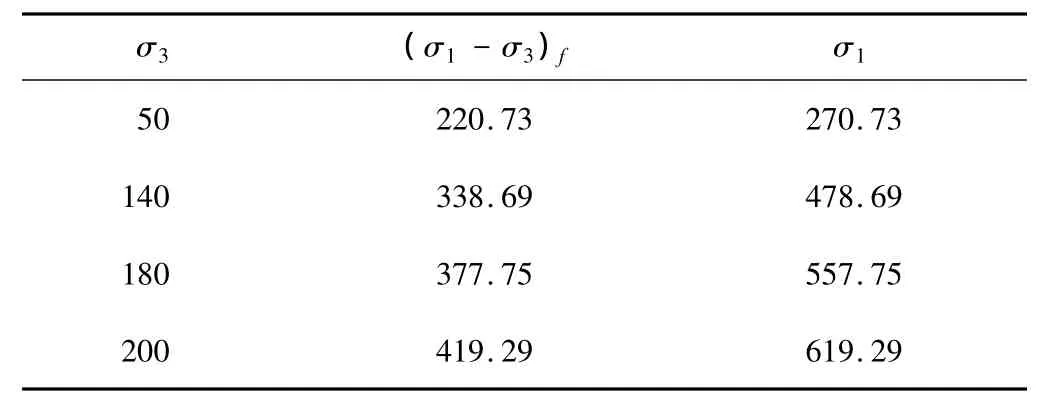
表3 不同围压下的最大应力值Table 3 Maximum stress under different confining pressure kPa

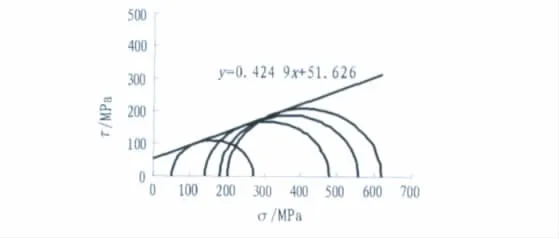
图5 老黏土不同围压下的莫尔圆Fig.5 Mohr’s circle of old clay under different confining pressure

2)Rf值确定。由式(3)绘制曲线如图6所示，不同的围压和卸荷比下几乎所有曲线都有良好的线性关系，这也证明式(4)能够很好地接近试验结果，表明老黏土在卸荷条件下的应力－应变关系能由双曲线表示。

根据式(3)对试验结果进行双曲线函数关系分析，可以通过应力应变关系的线性关系求得双曲线模型中的参数a和b。

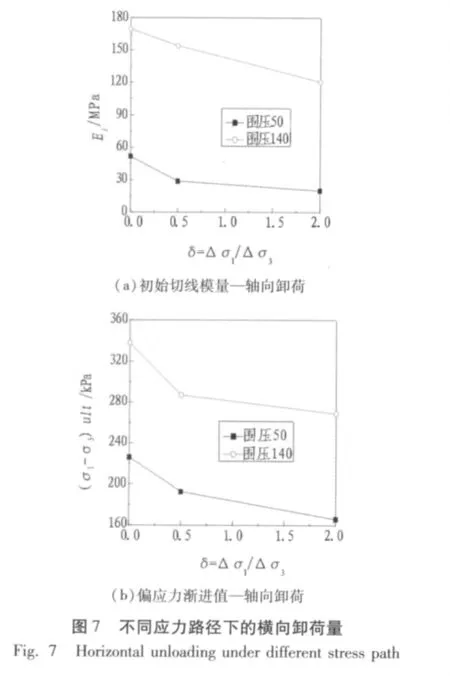
图7(a)为不同卸荷应力路径下，初始切线模量Ei随着轴向卸荷量的增加而逐渐减小，基本为线性减小。图7(b)为偏应力渐进值(σ1－σ3)ult随着轴向卸荷量的增加而逐渐减小，但并非线性减小。

由于轴向卸荷量反映了试样受扰动的程度，轴向卸荷量较小的试样受到的扰动程度较小;反之试样受到的扰动程度较大。故图7说明了卸荷扰动对土体的性质有较大影响。

3)K，n值确定。取大气压 =103.3 kPa，求得各围压下的lg(Ei/pa)和lg(σ3/pa)值，并以lg(Ei/pa)为纵坐标，以lg(σ3/pa)为横坐标绘制于双对数坐标系中，根据 lg(Ei/pa)=lgK+n·lg(σ3/pa)，可求出K，n的值。

若将所有试验拟合，得 lg(Ei/pa)=2.340 8+0.409 lg(σ3/pa)，故取 K=219，n=0.409，拟合表达式的相关性较差R2=0.423 8。

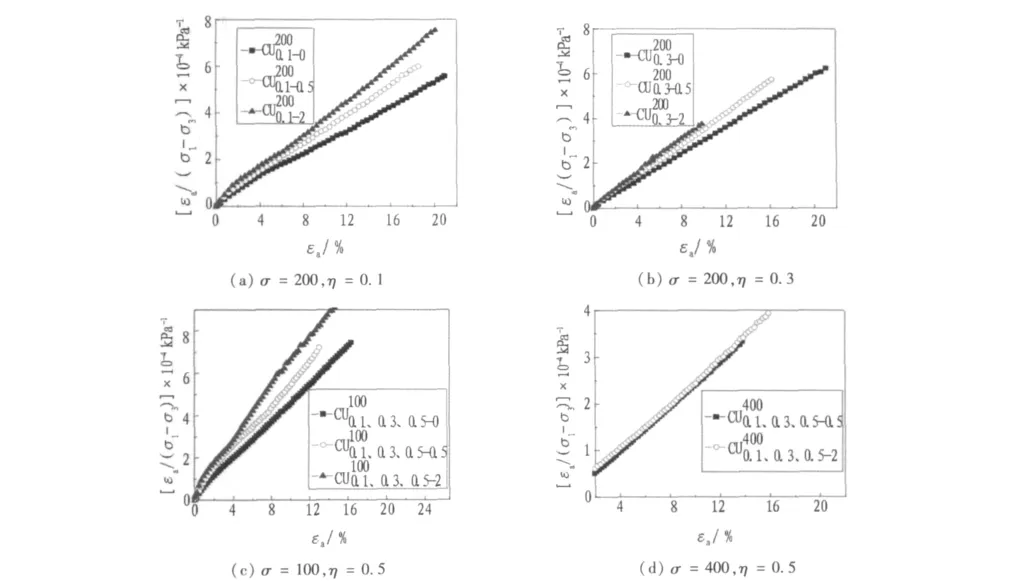
图6 剪切阶段εaσ3/(σ1－σ3)与εa关系曲线Fig.6 εaσ3/(σ1－ σ3)～ εacurves under shearing

由lg(Ei/pa)和lg(σ3/pa)的拟合结果可知，K、n值离散性较大，分析其原因主要有以下几点:

①本试验经历了不同的卸荷过程，从结果可知，卸荷比和应力变化比的大小对试样的初始切线模量有较大影响。

②原状土取样的离散性较大，本试验土样取自2个钻孔不同深度的土层，本身土样的性质不同。

③原状土样在取样、运输、切削、装样等过程中存在人为误差。

综合上述对Duncan－Chang模型中各参数的讨论结果，各参数的建议值如下:c为51.6，φ为23.1°，Rf为0.98，K 为181，n 为0.355。该试验结果对探讨工程中参数的获取方式将有一定的参考价值。

3 结论与讨论

利用应力路径三轴仪对武汉地区具有代表性的老黏土进行固结不排水三轴试验，研究了不同卸荷下土体的强度和变形规律，并从归一化应力－应变曲线出发，验证了适合武汉老黏土的非线性弹性模型，并对模型中的各个参数进行确定，试验结果表明:

1)老黏土不同卸荷比下的偏应力随轴向应变的增加而增大，偏应力－轴向应变曲线基本相似，呈应变硬化状态，这可能与老黏土的结构性有关。

2)武汉老黏土具有归一化性状。由于试样的不均匀性及试验步骤上的某些差别，归一化曲线有些差异，但对于相同剪切方式，不同初始固结应力的土体其归一化强度基本一致;对于不同剪切方式的土体归一化强度会有所差异。

3)本文所用的Duncan－Chang模型参数少，而且意义非常明确，易于确定，对工程应用有一定的参考价值。

［1］ 李芳.武汉市东西湖区老粘土的工程地质特性浅析［J］.土工基础，2004(3):55 －56.(LI Fang.The geological characteristic of old clay in Dongxi Lake in Wuhan［J］.Soil Engineering and Foundation，2004(3):55 －56.(in Chinese))

［2］ 艾传井，唐辉明，罗红明，等.武汉市青山地区老黏土的变形参数及承载性能研究［J］.中国水利水电，2006(8):72 －77.(AI Chuanjing，TANG Huiming，LUO Hongming，et al.Research on the deformation parameter and bearing performance of paleo-clay in Qingshan area of Wuhan［J］.China Rural Water and Hydropower，2006(8):72 － 77.(in Chinese))

［3］ 谭松林，王江.老黏土地基承载力的确定［J］.地质科技情报，2007(4):76 －78.(TAN Songlin，WANG Jiang.Determination of the bearing capacity of aged clay groundsill［J］.Geological Science and Technology Information，2007(4):76－78.(in Chinese))

［4］ 尹旭.武汉经济技术开发区老粘土基本物理力学参数统计分析［J］.资源环境与工程，2008(S2):57－60.(YIN Xu.The statistical analysis of old clay’s physical and mechanical parameters in Wuhan economic and technological development zone［J］.Resources Environment＆ Engineering，2008(S2):57－60.(in Chinese))

［5］ 曾义.武汉市老粘土内发现剪切滑裂面［J］.湖北地矿，1998(3):23 －26.(ZENG Yi.Discovery of the shear sliding-face in the aged soil in Wuhan city［J］.Hubei Geology ＆Mineral Resources，1998(3):23－26.(in Chinese))

［6］ 朱百里，刘国彬.软粘土深开挖的弹塑性分析［C］//中国土木工程学会第六届土力学及基础工程学术会议论文集.上海:同济大学出版社，1991.(ZHU Baili，LIU Guobin.The elastic-plastic analysis of soft clay in deep excavation［C］//China civil engineering society soil mechanics and foundation engineering academic conference.Shanghai:Tongji University Press，1991.(in Chinese))

［7］ 陈永福，曹明葆.上海地区软粘土的卸荷－再加荷变形特性［J］.岩土工程学报，1990，12(2):9－18.(CHEN Yongfu，CAO Mingbao.The deformation characteristics of soft clay under unloading and reloading in shanghai［J］.Chinese Jounal of Geotechnical Engineering，1990，12(2):9－18.(in Chinese))

［8］ 张文慧，王保田，张福海.应力路径对基坑工程变形的影响［J］.岩土力学，2004，25(6):964－966.(ZHANG Wenhui，WANG Baotian， ZHANG Fuhai. Influence of stress paths and consolidation stress ratios on soil’s deformation characteristics［J］.Rock and Soil Mechanics，2004，25(6):964－966.(in Chinese))

［9］ 张勇.武汉软土固结不排水应力－应变归一化特性分析［J］.岩土力学，2006，27(9):1509 －1513.(ZHANG Yong.Normalized stress-strain behavior of Wuhan soft clay［J］.Rock and Soil Mechanics，2006，27(9):1509 － 1513.(in Chinese ))