三坐标测量机在风电齿轮箱行星架加工中的应用

大连华锐重工集团股份有限公司通用减速机厂（辽宁 116000）张本麒 郝丽格 陈世刚 徐书岭

随着风力发电机组向大型化发展，对齿轮箱寿命和可靠性的要求也越来越高，对风电齿轮箱零件的加工精度要求也越来越高。行星架是风电齿轮箱的重要零件，行星架轴孔位置度精度直接影响齿轮箱的载荷分布是否均匀、运转是否平稳、转矩传动能力及噪声值指标，提高行星架的轴孔位置度精度对整个增速机运行十分必要。在本文中举例的某大兆瓦级风电齿轮箱，其行星机构的传动载荷不均匀系数kc为1.35。

为了保证行星架位置度精度，我厂在风电行星架加工时结合三坐标测量机进行行星架的位置度检测，并根据检测结果，对数控镗床等加工设备进行程序补偿，从而大大提高了行星架的位置度精度。同时，我们充分利用三坐标测量位置度的特点，基于最大值极小化思想，采用对三坐标位置度检测结果进行优化处理的方法，解决了一系列生产中遇到的零件的位置度加工和测量问题，挽救了许多濒临报废的零件，明显降低了行星机构的传动载荷不均匀系数kc，为公司产生了巨大的经济效益。

1.利用三坐标检测结果对数控镗床进行程序补偿

三坐标测量机检测零件的位置度采用的是坐标测量的方法，测量时，按照零件上的检测基准，测量机可自动建立一个三维校正坐标系，很方便地把零件上各孔的位置坐标量出来，并把位置度计算出来。三坐标测量机测量位置度不仅准确性好，而且可精确测量出各孔坐标偏差的具体数值和方向，对现场生产有很好的指导作用。

（1）位置度误差值的计算方法 孔的实际轴线的位置度误差值是以被测实际轴线的理想位置定位，做实际轴线的最小包容区域（圆柱面），该最小区域的直径即为孔的位置度误差值。

（2）位置度误差值的分析及应用 如图2所示的行星架，为我公司某兆瓦级风电齿轮箱的二级行星架，我们以此行星架为例，介绍一下我公司是如何利用三坐标测量机来提高行星架的位置度精度的。

由图样可以看出，此行星架为5孔均布，每孔分上、下两孔，理论中心距为817mm，相对于基准A、B的位置度要求为f0=φ0.05mm。

第1步：在数控镗床上，根据图样给出的各孔的理论位置，对行星架进行试加工，各孔可留量。

第2步： 对加工完成后的行星架进行三坐标检测。三坐标测量机根据图样给出的基准A、B建立坐标系，如图2所示。对三坐标位置度测量结果分析如表1所示。

根据表1，可得出各孔的实际位置与理想位置的偏差f，并可以得出偏差的数值及方向。

表1 行星架三坐标测量结果分析 （单位：mm）

但仅一次的测量结果，对生产实际的指导意义并不大，我公司一般采用多次测量对比分析得出结论来指导生产。如表2所示，为3下孔五次测量结果的对比。

表2 3号下孔五次三坐标结果对比 （单位：mm）

第3步：对表2数据进行分析。其中序号4的测量结果，明显分离其余四次，可被排除。其余四次的测量结果，其偏差的数值及方向有较好的一致性。其一致性，反映了机床在加工3号下孔时，有一致性很强的误差，则在实际生产时，可将其误差值进行程序补偿，提高机床加工精度。

第4步：对数控镗床程序进行补偿。

关于补偿数值，可计算各偏差的平均值，

则3号下孔的补偿数据为：

则补偿后3号下孔的程序为：

第5步：其他各孔分别得出补偿数据后，对机床程序进行补偿。利用补偿后的程序，将以上各试验行星架，按成品尺寸进行加工，并进行三坐标位置度检测。

以上利用三坐标进行行星架加工程序补偿的方法，在实际生产中得到了很好的验证，对提高行星架的位置度精度效果十分显著，明显提高了零件的合格率，降低了企业成本。

同时，以上方法在实际操作中，有以下注意事项：①严格控制机床周围的环境温度。最好有恒温加工车间，室温常年控制在（20±1）℃。②严格控制三坐标测量机的环境温度。最好有恒温测量车间，室温常年控制在（20±1）℃。被测零件在测量车间需放置24h以上，使其温度与恒温车间一致后再进行三坐标位置度测量。③机床上的胎具、夹具等工装零件，在机床调整过程中及调整完成后，不得随意改动。若改动，需重新进行三坐标检测及程序补偿。④行星架各孔加工及检测顺序要固定，不得随意更改。

2.行星架三坐标检测结果的优化方法

位置度的定义：以被测实际轴线的理想位置定位，做实际轴线的最小包容区域，该最小区域的直径为孔的位置度误差值。

分析位置度的定义，其要求包容区域为最小，该性质称为“定位最小区域准则”。

仍以图2行星架为例，在三坐标测量机建立坐标系时，以过1号孔的实际中心点来确定X、Y轴，这就可能使直接获得的检测结果偏离“定位最小区域准则”。因而，在实际测量工作中对行星架的此类问题的数据处理与评定一定要慎重，避免误判而给企业造成损失。如果按照一次测量就下结论，该行星架就有可能报废，但在许多情况下，根据位置度公差三坐标测量原理是可以通过对基准坐标系旋转来优化测量结果，使之得出符合图样和工艺要求的位置度测量结果。

以下，仍以图2行星架为例，举例说明三坐标检测结果的优化过程。

（1）检测数据分析 某行星架的三坐标检测结果如表3所示。

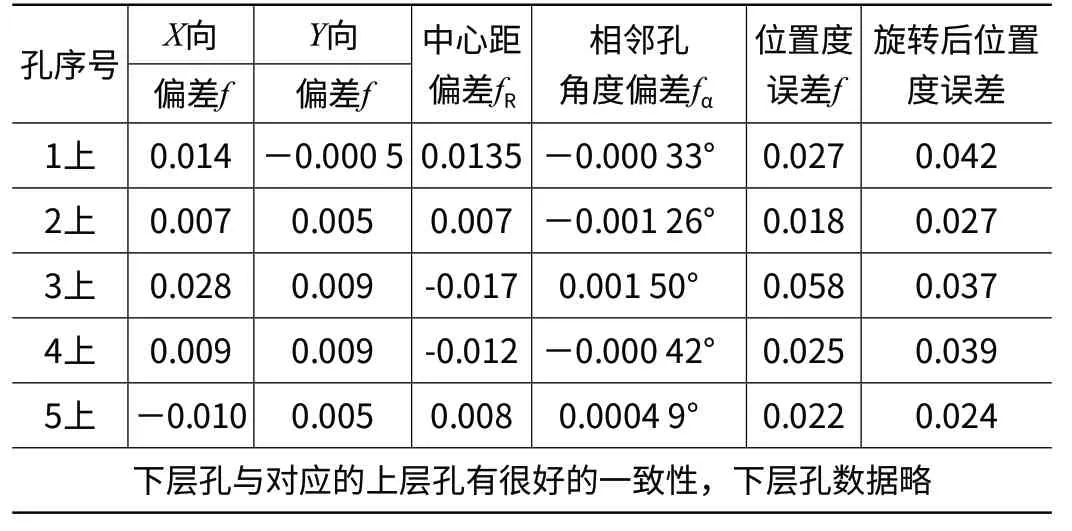
表3 某行星架三坐标测量结果 （单位：mm）

对表3的数据做如下进一步分析。首先判断各孔位置度测量值在初始坐标系下是否有可能满足公差要求，首先判断各孔的中心距偏差fR的2倍是否小于所要求的位置度公差值f0，若大于，则该行星架位置度肯定超差，该零件不合格，没有必要进行下一步，直接报废。若小于须进行下一步分析，方可对初始坐标系进行旋转，在旋转后的坐标系下重新评价各孔位置度。根据表3数据，本行星架满足坐标系旋转条件。

（2）旋转量的确定 从表3中5孔的角度偏差fa中找出角度偏差中的最大值fαmax及最小值fαmin，然后得出坐标系的最佳旋转量。

坐标系的最佳旋转量

该行星架的坐标系最佳旋转量Q=0.0015°－│－0.00033°│=0.00117°

坐标旋转方向与fαmax方向一致，故原始坐标系绕原点逆时针方向旋转0.00117°，得到新的坐标系，如图3所示，在新坐标系下，各孔的位置度见表3中f 所示，各孔位置度均合格。通过这样的坐标系旋转处理得到的位置度才符合各孔的实际位置度误差“定位最小区域准则”。

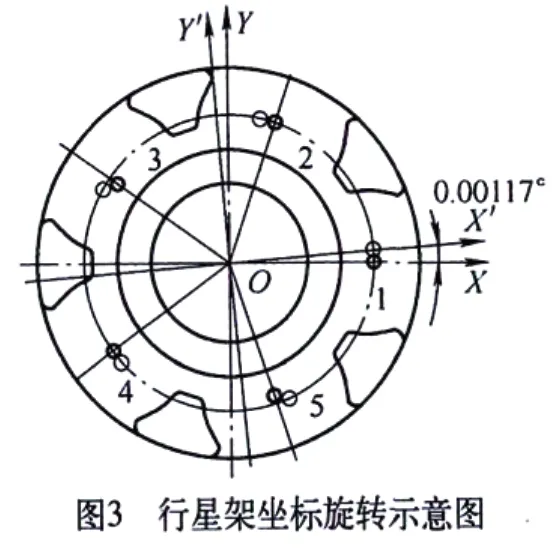
可见，我们在使用三坐标测量均布孔系的位置度时，一定要注意测量坐标系的优化处理，以便使测量结果符合位置度误差最小区域法的评价原则，避免合格零件的报废，为企业产生巨大的经济效益。

3.结语

行星架是风电齿轮箱中关乎整机运行稳定的关键零部件，其位置度误差要求十分严格。企业在正确使用三坐标测量机进行程序补偿后，明显提高了行星架的位置度合格率，降低企业成本。

同时，对已通过程序补偿，但一次检测位置度仍不合格的行星架，通过对初始坐标系的旋转来分析、优化初始坐标系下的测量结果，得到符合位置度误差最小条件的测量数据，避免了合格零件的报废，这对于降低企业成本，保证产品质量，提升企业的竞争力有非常积极的意义。

通过以上提高行星架位置度的方法明显降低了行星机构的传动载荷不均匀系数kc。该大兆瓦级风电齿轮箱在试验台进行满载荷试验时，通过在齿面贴应变片得到的行星机构的传动载荷不均匀系数kc为1.15，明显低于设计要求的1.35，也使该齿轮箱顺利通过了德国劳氏船级社GL认证。这使得我公司成为迄今为止国内首台获得大兆瓦级别风电齿轮箱权威认证的企业，为公司风电产品在国内及国际市场竞争力提供了有力的保证。