城市公交客运量预测的线性测量误差模型

乔路芳，乔路娜

（1.中国矿业大学 理学院，江苏 徐州 221116；2.山西省襄垣一中，山西 长治 046200）

所谓预测指的就是人们对未来的事物或未知时间的行为和状态作出的主观上的判断.然而，一切正确的预测都应该建立在对客观事物的过去和现状进行深入研究和科学分析的基础上，并同时利用一种逻辑结构将其与未来的情况联系起来，用来达到预测的效果[1].城市公交客运量系统可以看作为一个灰色系统，其中的公交客运量又是一个随机变化的灰色量[2]，它受到多种关联因素的影响和制约，例如该市的职工人数，居民的零售额和职工收入等.

测量误差模型是我们经常会遇到的一类模型，它的优点主要是可以考虑原始数据的测量误差，因此该模型在很多领域都有应用，但在城市公交客运量预测方面还没有见到.本文以某市1998～2007年城市公交年客运量及该市的职工人数、居民零售额和职工收入作为原始数据，建立了城市公交客运量预测的线性测量误差模型，并对该市2008年、2009年和2010年的公交客运量进行了预测，最后与实际值进行对比，拟合结果对比表明，线性测量误差模型预测精度较高.

1 模型的建立与分析

设Y为公交年客运量，X为影响客运量的几个变量组成的矩阵，X有一定的误差，其期望为Z且未知，则可得到如下线性测量误差模型[3-4]：

式中：f是已知的函数；yi是观测响应变量；Z是n×p阶第i行为zTi的矩阵；In是n阶单位矩阵；β是p维未知参数；X是n×p阶第i行为xTi的矩阵；σ2是未知参数；Λ是已知的非负定矩阵；εi是测量值的随机误差；ξ是n×p阶矩阵.

因为X和Z是两种不同性质的协变量，X是测量值，而Z未知，所以我们可以用Nakamura的校正似然法来处理此类测量误差问题.

设 l(β,Z,Y)，U(β,Z,Y)，J(β,Z,Y)和 I(β,Z,Y)分别为模型的对数似然函数，得分函数，观察信息及 Fisher信息.记E+为Y的数学期望，其中

则根据得分函数的性质有E+U(β,Z,Y)=0.校正似然函数l*(β,X,Y)需满足条件[5]

其中 E*表示 Y 给定时关于 X 的条件期望. 设 U*(β,X,Y)=∂l*(β,X,Y)/∂β ，J*(β,X,Y)=-∂U*(β,X,Y)/∂β ，I*(β,X,Y)分别为校正得分函数，校正观察信息和校正Fisher信息.如果E*与∂β可以交换，则

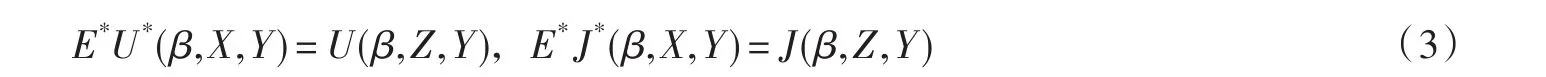
参数 β 的估计满足条件U*(,X,Y)=0，称为校正最大似然估计（CMLE）[6].记E=E+E*，显然有

这表明校正得分函数是无偏的.对于上述的正态测量误差模型（1），Nakamura证明了参数估计的渐近正态性和相合性，而且有

将上述结果应用到模型（1），则对数似然函数为

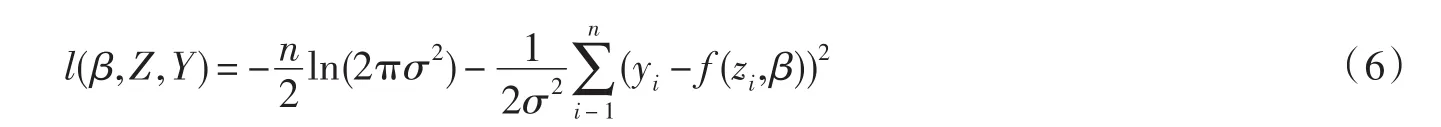
校正似然函数可表示为

通过计算可知E*l*(β,X,Y)=l(β,Z,Y).因为校正似然函数性质比较好，根据它可很容易求出参数 β的CMLE.

特别地，如果式（1）中 f(xi,β)=xTiβ，那么将式（7）对 β求导，得

其元素为hij，=Y-为残差向量.σ2的估计为=||||2/(n-p).则由（7）式可知，校正Fisher信息阵为 I*(β,X,Y)=σ-2(XTX-nΛ).

从上述可以知道校正似然法也可以应用于一些广义的线性模型及其非线性模型.

2 实例验证

2.1 模型的建立

城市公共交通系统可以用测量误差模型来描述，而测量误差模型也可以说是个多元回归模型，多元回归模型中自变量可以用关联分析的方法进行选取.公交客运量是一个随机变化的量，它受到很多种关联因素的影响、制约，如职工人数、居民零售额、职工收入、公交线路条数及总长度、公交车辆数、公交客运收入等.利用文献[2]提供的关联分析的方法，职工人数、居民零售额和职工收入是影响城市公交客运量的前三位优势因素.

以某市1998～2007年的公交年客运量、职工人数，居民零售额和职工收入（见表1）为原始数据[7]，建立公交年客运量预测的线性测量误差模型，与普通线性回归模型进行比较，并对该市2008、2009、2010年的公交客运量进行预测.

分 析 过 程 中 ，采 用 yi=β0+β1xi1+β2xi2+β3xi3+ εi，其中 i=1,2,3,...,10.xi～N(zi,λ). 由Λ是已知非负定矩阵，这里采用λ服从标准正态分布.为使得（7）式达到最大，应用Matlab编

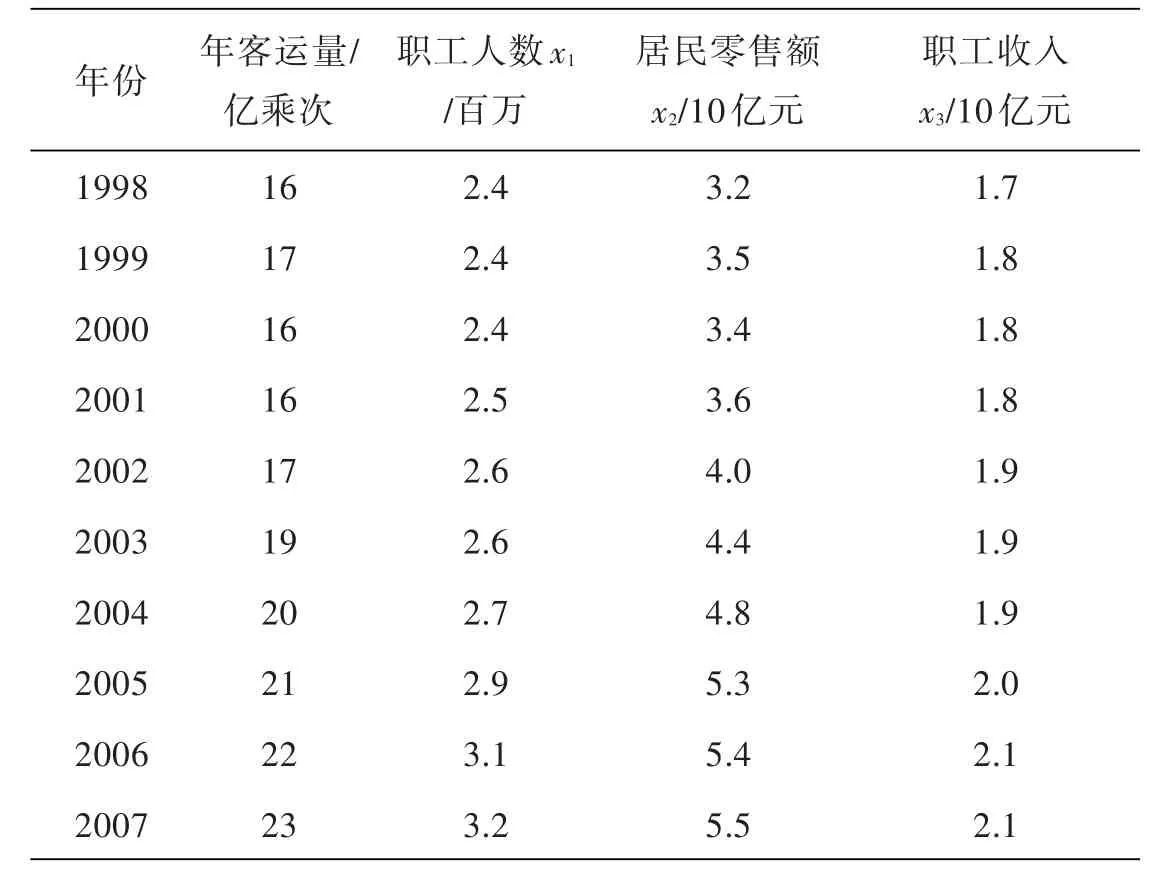
表1 某市年客运量数据

写计算程序得到 β和 σ2的参数估计分别为0=0.5613，1=1.6291,2=2.8284，3=1.1283，σ2=1.1334.该市公交年客运量的预测线性测量误差模型为：

经计算，普通线性回归模型为：

式中y为年客运量，x1为职工人数，x2为居民零售额，x3为职工收入.

2.2 预测

根据该市社会经济发展的规划，运用（11）式和（12）式对2008、2009、2010年该市的公交年客运量进行预测，同时根据“3σ准则”确定预测区间，并与实际值进行对比，预测结果见表2（x1为职工人数，x2为居民零售额，x3为职工收入）.

从表2可以看出，通过测量误差模型和普通线性回归模型分别对城市公交客运量进行预测，并与实际值进行对比，测量误差模型的预测精度较高.

表2 年客运量预测表

3 结 语

目前我国大多数城市的交通仍然是以客运为主的，然而城市公共交通的合理规划和快速健康的发展又要建立在公共车辆客运量科学预测的基础之上.本文以某市1998～2007年城市公交年客运量及该市的职工人数、居民零售额和职工收入作为原始的数据，通过考虑原始数据的测量误差，建立了城市公交客运量预测的线性测量误差模型，并对该市2008年、2009年、2010年的公交客运量进行了预测，并且把预测的结果与实际值进行对比，拟合结果表明，线性测量误差模型的预测精度比较高，因此它的预测结果可以为城市公共交通合理规划和发展提供依据.

[1]姜华平，陈海泳.城市公交客运量的预测模型研究[J].理论新探，2005，6（12）：1-2.

[2]李群.我国城市公交客运量的关联分析[J].苏州市职业大学学报，2007，18（4）：1-3.

[3]贾仁甫，陈守伦，丁鑫.需水量预测的线性测量误差模型[J].河海大学学报，2008，36（4）：1-2.

[4]赵俊.需水量预测的测量误差模型[J].扬州大学学报，2009，12（3）：1-2.

[5]FULLER W A.Measurement error models[M].New York：Wiley，1987：1-10.

[6]宗序平.线性测量误差模型及其诊断[J].系统工程学报，1999，14（2）：1-2.

[7]张雅君，刘全胜，冯萃敏.多元线性回归分析在北京城市生活需水量预测中的应用[J].给水排水，2003，29（4）：1-3.