考虑转矩波动的电动汽车悬架NVH性能参数优化*

李程祎，左曙光，段向雷

(同济大学新能源汽车工程中心，上海 201804)

前言

作为电动汽车的一种重要形式，轮边驱动电动汽车依靠独立电机驱动单个车轮，并将驱动电机布置在车架或悬架上(而不同于轮毂驱动直接集成在轮胎内的形式)，从而使等效非簧载质量大幅减小，较好地解决了非簧载质量过大带来的平顺性问题[1];通过精确的电子控制来实现理想的车辆稳定性控制(如牵引力控制、制动防抱死控制和横摆稳定性控制等)，从而改善了车辆的行驶性能。

汽车的NVH性能是衡量汽车水平的一个重要指标[2]。但由于受到供电电流谐波分量、磁场的非正弦分布、定转子偏心、定子开槽和电机控制系统测量误差等因素的影响，电机输出转矩存在一定幅度的波动[3]。而波动的转矩直接作用在轮胎上，引起轮胎与地面间纵向和垂向作用力的冲击与波动，从而导致整车纵向和垂向的振动问题。有研究表明[4－5]，驱动电机的 1、2和 6阶转矩波动是车身结构振动和车内噪声的主要激励源，且激励峰值频率分布在30～280Hz的中高频范围内。

对此，许多学者进行了深入的研究。有些学者就转矩波动的来源入手，从电机控制的角度出发研究如何抑制电机的转矩波动[6－7];还有些学者尝试通过在电机输出端加入扭转减振器，试图从传递途径的角度来衰减转矩波动。本文中从轮胎-悬架系统的角度出发，将悬架作为轮胎和车身之间的隔振元件考虑。首先在Adams中建立悬架-轮胎-路面多体动力学模型;然后通过响应面法对性能参数进行第1次优化和灵敏度分析;最后对灵敏度较高的参数用梯度下降法进行第2次优化。最终的优化结果明显减小了转矩波动对车身振动的影响。

1 悬架-轮胎-路面多体动力学模型的建立

要想正确分析转矩波动对悬架NVH的影响，首先在Adams/View中建立准确的悬架-轮胎-路面多体动力学模型。为了排除前、后悬架间振动的耦合，只建立基于后悬架的多体动力学模型。

1.1 悬架模型

本文的研究对象是某轮边驱动电动汽车，其后悬架三维模型见图1。该车后悬架为扭转梁结构，采用电机加两级斜齿轮减速器的驱动形式。减速器的壳体同时也是悬架的纵臂，减速器输出端连接车轮，驱动电机用螺栓固接在减速器壳体上并驱动减速器输入端。中间一根扭转梁分别连接左右悬架的纵臂。

根据三维模型关键硬点和拓扑结构，在Adams/View中建立后扭转梁悬架模型，并做了如下简化:

(1)所有零部件均为刚体，各部件的惯量参数和质心位置从三维模型中测取;

(2)纵臂与车身间、减振器上端与车身间通过衬套连接;减振器用Spring元件简化;中间的扭转梁用Torsion Spring元件简化;且各弹性元件参数均做线性化处理;

(3)车身以刚体代替，并且车身与大地之间通过平行副连接，即只限制车身俯仰和横摆自由度，其余自由度不做限制。

1.2 轮胎路面模型

由于须进行的是平顺性仿真，且要分析的频率较高，因此轮胎模型选择Ftire。它是一种基于柔性环理论、完全非线性的轮胎模型。其适用频率高达120～150Hz，且仿真精度较高，是MSC公司官方推荐的进行平顺性和耐久性仿真的轮胎模型[8]。

在使用Ftire时须注意的是:为了发挥其精度优势，Adams积分器积分最大步长Hmax设置为0.001s。

为了排除转矩波动以外的激励对车身振动的影响，本文中选择平直路面。

1.3 转矩波动模型

在纵臂和车轮之间定义单向转矩，作用方式为Two Bodies，即准确模拟轮胎与减速器之间的作用转矩和反作用转矩。

建立考虑转子磁场前3阶谐波影响的永磁同步电机转矩模型[9]为

式中各符号含义及取值见表1。

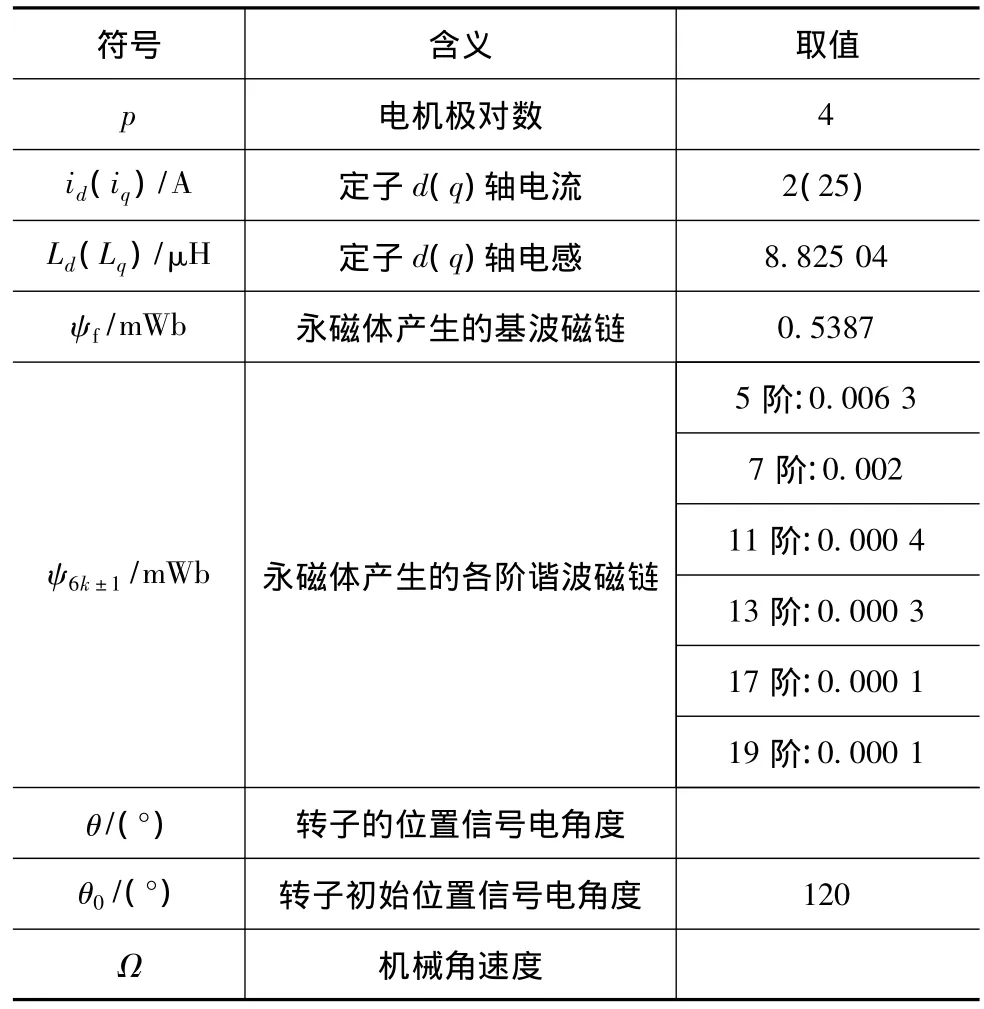
表1 转矩dq模型符号

转矩时域曲线如图2所示。

1.4 完整模型

最终建立的悬架-轮胎-路面多体动力学模型共有5个刚体(左右纵臂、左右减振器上支撑盖和车身)、30个自由度，如图3所示。

2 悬架性能参数的两次优化

悬架的结构参数(如硬点位置)主要影响悬架的运动学特性，而悬架的性能参数(如弹性元件参数)主要影响悬架的弹性运动学特性[10]。本文的目的是优化悬架的NVH性能，故对悬架性能参数进行了两次优化，具体流程如图4所示。

2.1 响应面法优化

响应面法是一套数学与统计学相结合的方法，是用一个超曲面来近似替代实际复杂结构的输入与输出关系的方法[11]。其基本方法是进行若干次试验，用最小二乘法回归模型在优化目标和优化因素之间拟合出一个定量的一次或二次多项式，即响应面。有了响应面，就可不用再进行额外的仿真，只须对表达式用数学的方法求极值，就能算出最优解和对应的因素取值。

进行响应面法分析一般遵循以下5个步骤:(1)定义优化目标;(2)选择一系列变量作为优化因素;(3)确定各因素的变化水平，根据策略设计试验表;(4)进行试验，记录试验结果;(5)分析试验结果，进行优化。

本文中采用的具体步骤如下。

(1)考虑到人体对不同频率的振动敏感程度不同，参考 ISO2631—1:1997的规定，选择0～120Hz频率范围内车身质心垂向加权加速度均方根值作为优化目标[12]。不同频率f的频率加权函数为

(2)所选取作为优化因素的悬架性能参数如表2所示，各因素变化范围为－50% ～+50%。

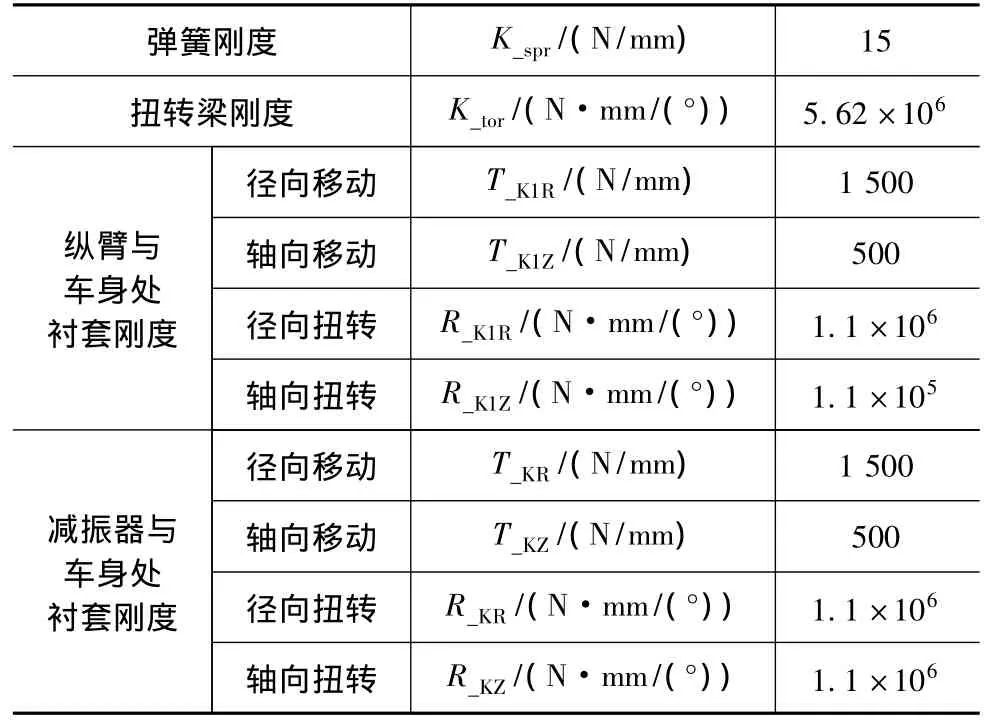
表2 弹性元件参数

(3)常用的试验设计方法有全因素法、部分因素法、中心复合设计(CCF)、D-最优设计和Box-Behnken。D-最优设计的根本思想是使XTX的行列式最大，其中X是试验因数输入矩阵[13]，其最少试验次数为(n+1)(n+2)/2，其中n是试验因素的个数。本文中选择D-最优设计，共进行100次试验。

(4)仿真由悬架波动的转矩驱动，在平直路面上直线行驶。仿真时间为10s，仿真步长为0.001s。

(5)响应面法优化后的悬架性能参数见表3。对响应面拟合结果进行模型适应性检查，得到复相关系数R2=0.962(大于0.95，满足要求)、修正的复相关系数R2

adj=0.923(大于0.9，满足要求)，表明拟合精度较高，结果可靠，可做进一步分析。

2.2 灵敏度分析

各性能参数灵敏度如图5所示。图中纵坐标指的是某因素取值发生变化后(其余因素仍取初始值)所引起目标值的改变量与目标原始值的比值。正负号表示因素对目标的影响是增大还是减小。因此，纵坐标绝对值越大，表明该因素对目标的影响越明显。由图可见，T_K1R和R_K1Z灵敏度相对较大。

2.3 梯度下降法优化

由于响应面法最高只是2次拟合，因此即使拟合精度足够高，用响应面法算出来的极值仍可能与目标的全局最优解存在一定的偏差。因此，有必要以这一优化为初始点再次进行优化，以便能更准确地找到全局最优解。优化因素就选择T_K1R和R_K1Z这两个灵敏度高的参数。

此处利用Adams自带的优化计算功能:优化方法选择梯度下降法;优化目标不变，其结果见表3。

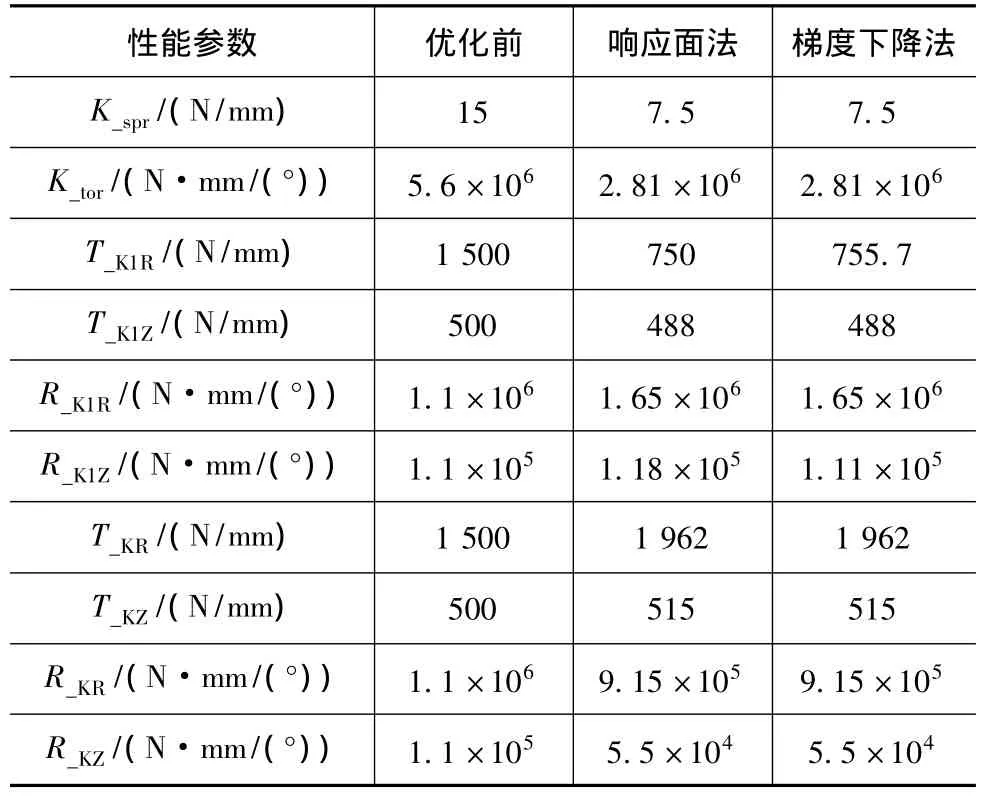
表3 性能参数优化结果

3 结果分析与对比

图6为优化前后质心垂向加速度的自功率谱。由图可见，优化后的功率谱在25～100Hz范围内的幅值明显降低，能量分布更均匀。

优化前、后的质心垂向加权加速度均方根值对比见表4。可见，经过两次优化后，下降了11.2%，车身振动明显减小。

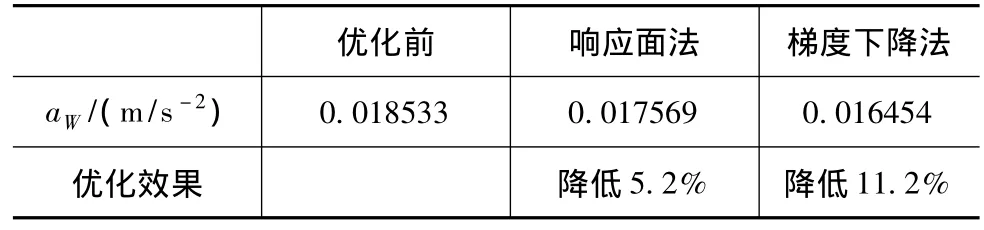
表4 垂向加权均方根对比

此外，通过响应面法和梯度下降法的优化效果对比可以发现，响应面法优化后的结果并不是全局最优的，其依然存在继续降低的可能性。从而说明本文中进行两次优化的思路是可行且必要的。

3 结论

(1)通过对悬架性能参数的优化，使车身振动能量降低，且在0～120Hz的频带内分布更均匀，明显改善了由于转矩波动引起的车身振动，提高了悬架的NVH性能。

(2)通过两次优化结果的分析与比较，可以看出单纯用响应面法得到的结果仍不是全局最优解，有必要通过后续的二次优化来求得全局最优解。

[1]陈辛波，钟再敏，唐峰，等．减小单纵臂悬架轮边电驱动系统等效簧下质量结构及方法:中国，102092256 A[P]．2011－06－15．

[2]李欣冉，陈晓新，王家恩，等．橡胶衬套对汽车悬架系统NVH性能影响研究[J]．合肥工业大学学报(自然科学版)，2012(5):581－584．

[3]张立军，钱敏，余卓平．轮毂电机-轮胎总成非线性动力学特性仿真分析[C]．第五届中国智能交通年会暨第六届国际节能与新能源汽车创新发展论坛优秀论文集(下册)．北京:电子工业出版社，2009．

[4]王建，张立军，余卓平，等．燃料电池轿车电机总成的振动阶次特征分析[J]．汽车工程，2009，31(3):219 －223．

[5]于增亮．轮毂电机驱动电动车悬架系统振动特性[D]．上海:同济大学，2010．

[6]陈冬雪，宗长富，何磊，等．轮毂电机的转矩脉动抑制方法研究[J]．科学技术与工程，2012(8):1811 －1815．

[7]刘和平，赵智辉，尹贤亮．新型轮毂电机转矩脉动抑制方法应用[J]．微电机，2011(3):21 －24．

[8]陈军．MSC．ADAMS技术与工程分析实例[M]．北京:中国水利水电出版社，2008．

[9]李景灿，廖勇．考虑饱和及转子磁场谐波的永磁同步电机模型[J]．中国电机工程学报，2011(3):60 －66．

[10]刘慧斌．Strut-Links型后悬架硬点及衬套刚度优化方法的研究[D]．长春:吉林大学，2011．

[11]王延克．基于响应面法的汽车悬架系统优化设计[D]．成都:西南交通大学，2009．

[12]陈晓新．基于刚柔耦合的整车动力学建模与悬架隔振性能分析[D]．合肥:合肥工业大学，2010．

[13]隋允康，宇慧平．响应面方法的改进及其对工程优化的应用[M]．北京:科学出版社，2011．