太原湖滨广场超高层结构的抗震性能化设计
樊永盛,王大斌
(太原市建筑设计院,太原 030002)
0 引言
太原湖滨广场综合项目是在原太原市湖滨会堂旧址上的改扩建工程。本项目建筑场地总用地面积为48 412 m2,总建筑面积约为19.14 万m2。地下3 层,地上由1 幢47 层塔楼和4 层裙房组成。塔楼与裙楼之间设有防震缝,缝宽取中震作用下的位移计算极值,为300 mm。主体与裙楼完全断开,形成各自独立的结构单元。主体塔楼的建筑总高度为208 m,属于超高层结构;裙房总高度为25.25 m,属于多层结构。

图1 建筑效果图
塔楼采用矩形钢管混凝土框架、钢筋混凝土筒体组成的混合结构体系,我国《高层建筑混凝土结构技术规程JGJ3—2010》[1](以下简称《高规》)规定的高度限值为150m。而室外地面到屋面的总高度为208m,超过规范限值38.7%。结构的高宽比为4.26,满足《高规》[1]规定的高宽比限值。平面布置中,由于建筑门厅的设置,造成二层楼面留有“L”形的洞口,局部楼板缺失面积达到31.8%,造成平面刚度急剧变化。根据我国《超限高层建筑工程抗震设防管理规定》(建设部令第111 号),塔楼为超限高层。
1 结构模型的建立
根据我国《建筑抗震设计规范GB50011—2010》[2](以下简称《抗规》)规定,计算程序采用ETABS(ver9.2.0)以及MIDAS/GEN(ver7.3.0)分别建立模型进行计算分析。
分析过程中,塔楼以地下室顶板作为嵌固端,板厚为180 mm。地下1 层的抗震等级与地上部分相同,地下2、3 层的抗震等级为三级。其他参数如下:
1)抗震设防类别为丙类,场地类别为Ⅲ类。
3)采用振型分解反应谱法计算结构响应,振型数取为15,各振型贡献按CQC 组合;周期折减系数取0.8。
4)考虑偶然偏心(计算控制位移比)和双向地震扭转效应组合工况。
5)整体分析时楼板假定为刚性楼板,2 层楼板进行单独分析时采用弹性楼板假定。
6)塔楼采用型钢钢筋混凝土筒体结构,框架的抗震等级为一级,抗震墙的抗震等级为特一级。
(1)时间因素(粒度精确到15分钟)。电力负荷的大小会随用电时间的峰谷而显著变化,因此,其属于时间序列数据,这也是使用LSTM算法可以高精度预测的原因,它在处理时间序列数据上有优秀的成绩。
7)设计使用年限为50 年,建筑结构安全等级为二级。
2 小震下结构弹性分析
2.1 振型分解反应谱法
分别使用两种软件对塔楼进行小震下的振型分解反应谱法计算,得出塔楼的各阶自振周期。
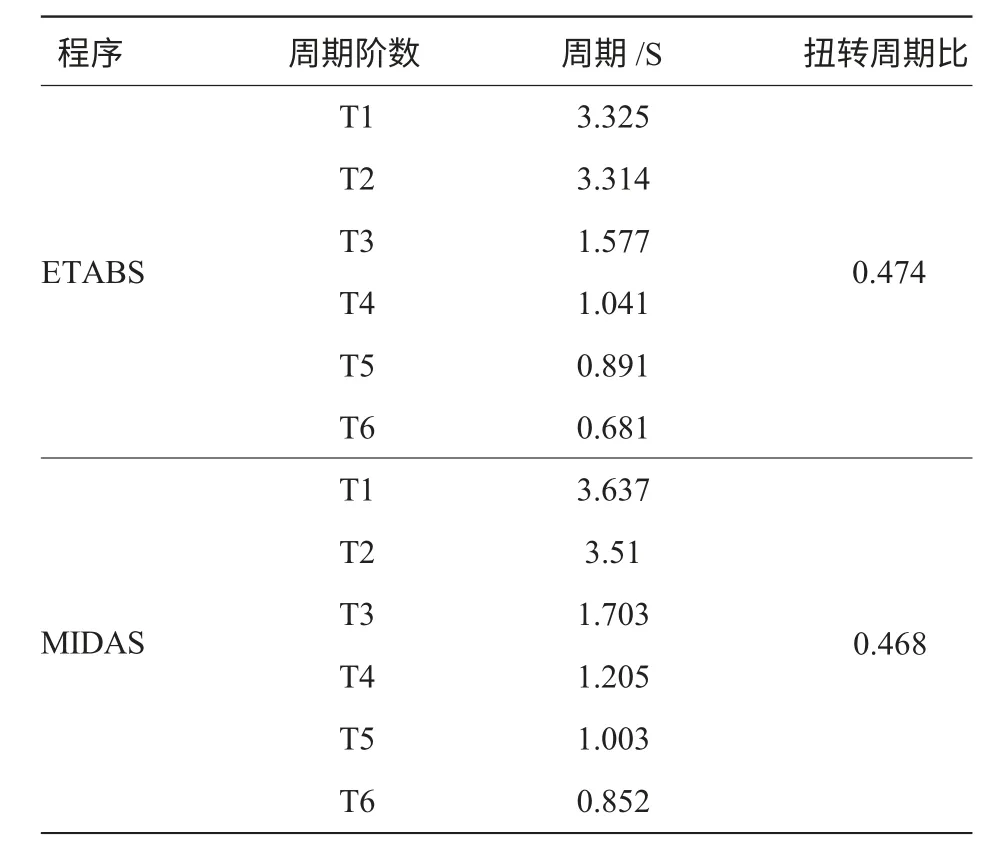
表1 塔楼各阶自振周期
由表1 可得,两个程序计算所得的各阶自振周期及扭转周期比数值接近,说明两个模型建立合理,能准确反映结构体型特点。
根据我国《高规》[1]第3.7.3 条第3 款,高度在150~250 m 之间的高层建筑,其最大层间位移角限值按高度在1/800~1/500 之间线性插入取值。可得本工程最大位移角限值为1/659。使用ETABS 及MIDAS 计算的结构层间位移角分别见图2 和图3。
由图2、3 可得,两个程序得出的层间位移角变化曲线基本一致。在设置了伸臂桁架的第24 层和第40 层,结构的层间位移角显著减小,可见伸臂桁架对层间位移角的控制作用显著。
由表2 可得,结构的最大层间位移角满足规范限值,说明抗震墙的平面布置较为合理。位移比限值均小于1.4,说明结构的扭转控制较好。且两个程序的其他计算结果也较为接近。说明两个模型的建立符合结构的受力特征。
2.2 弹性时程分析法
由于拟建高层位于Ⅲ类场地,且高度达到208 m,根据《抗规》[2]规定,应采用时程分析法进行多遇地震下的补充计算。计算中采用的地震波为一条人工模拟波和两条实际的强震记录(一条是1971 年2 月9 日的SAN FERNANDO 地震记录,另一条是1970 年9 月12 日的LYTLE CREEK 地震记录)。各地震波的波形如图4~9。
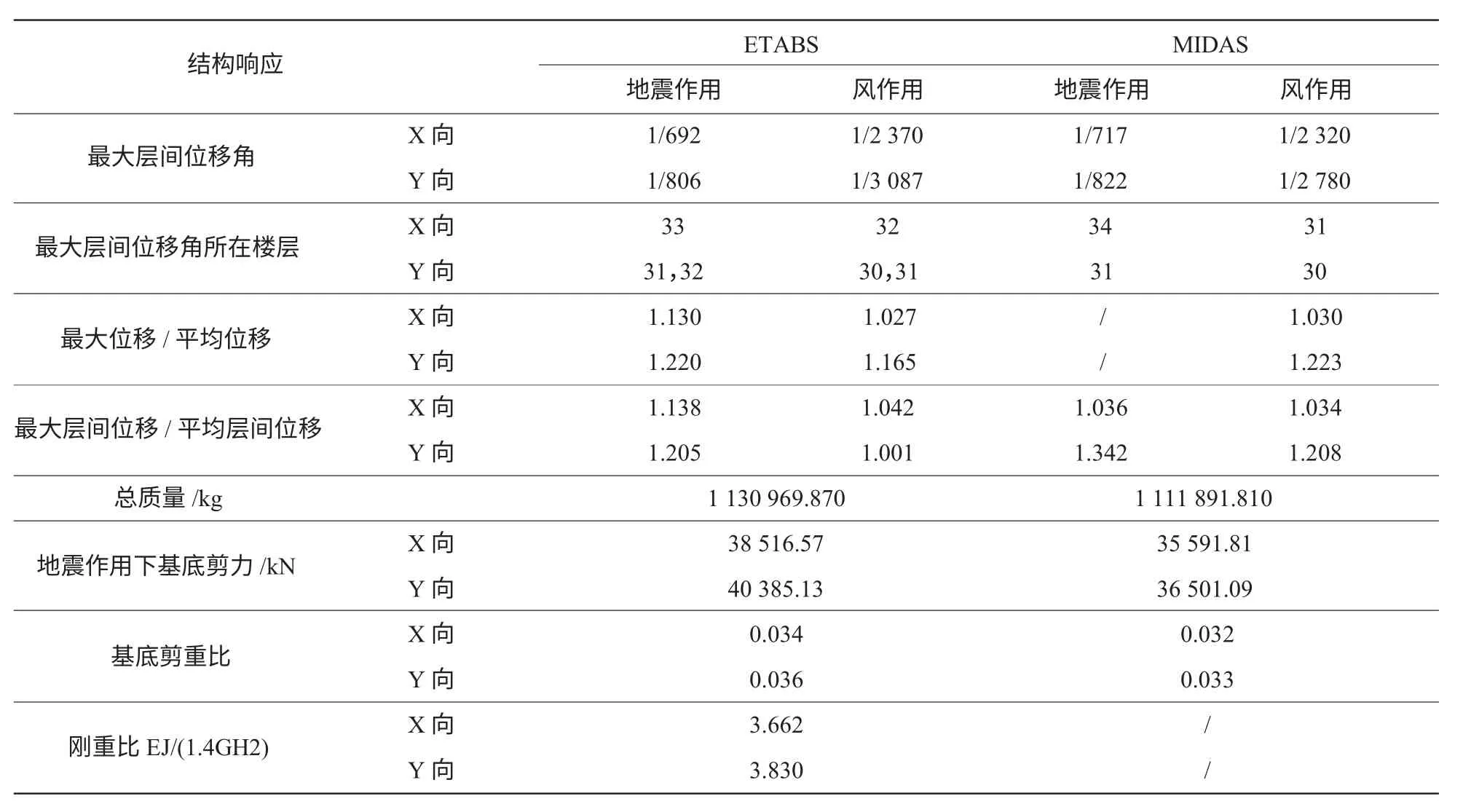
表2 ETABS 和MIDAS 部分计算结果对比

图2 ETABS 中X 向及Y 向层间位移角
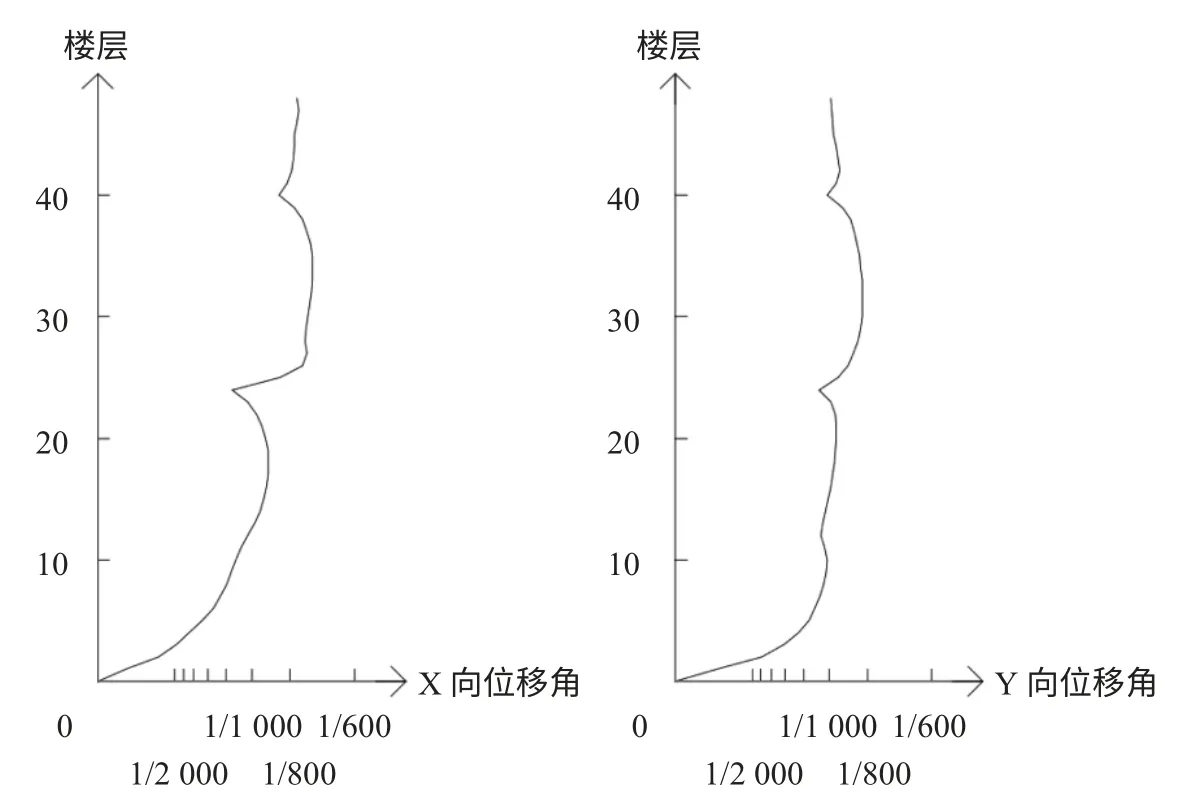
图3 Midas 中X 向及Y 向层间位移角
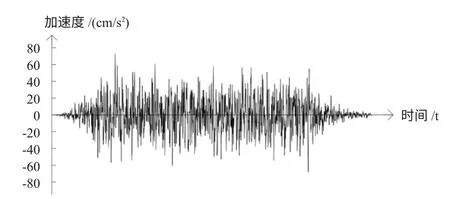
图4 人工波RGB 的X 向波形曲线

图5 人工波RGB 的Y 向波形曲线
弹性时程分析时,按照地面运动最大加速度为70 gal,对波形进行相应调整。由于反应谱计算时考虑双向地震作用,时程分析中的地震波也按照双向输入,主方向与次方向的水平分量比为1:0.85,取结构阻尼比为0.04 进行时程分析。由于地震波数据的时间间隔为0.02 s,持续时间最长的LYTLE CREEK波为49.46 s,故设置时程结果输出按0.2 s 步长,共250 步,以覆盖地震波作用全过程。
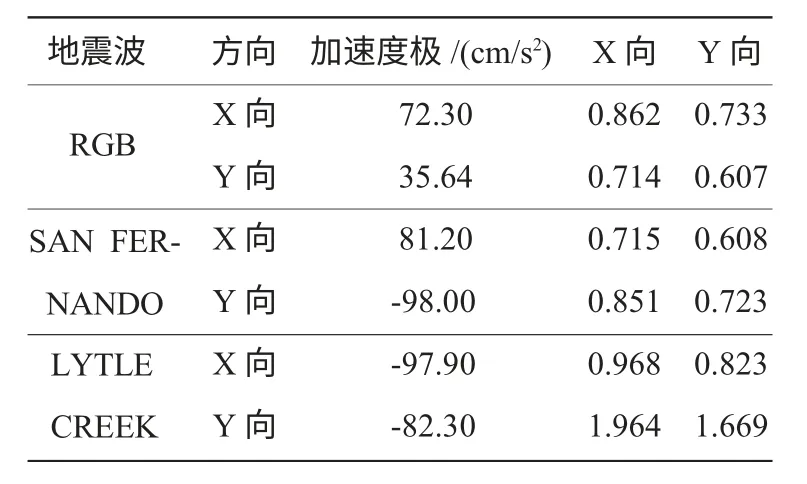
表3 时程分析中各条波的调整系数

表4 ETABS 弹性时程分析结果
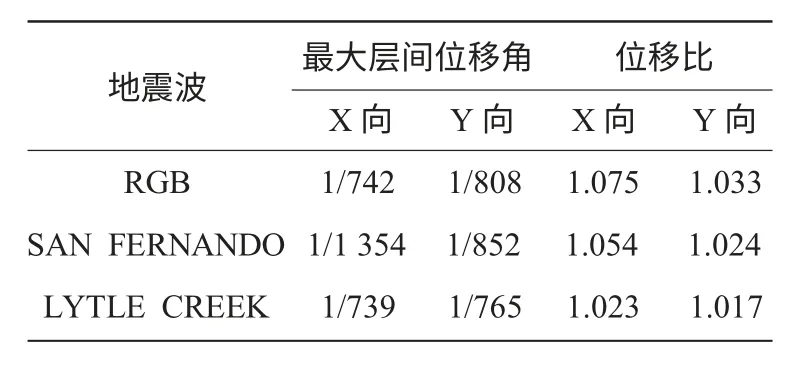
表5 MIDAS 弹性时程分析结果
由表中可以看出,结构弹性时程分析的结果满足规范规定。并且通过与振型分解反应谱法的结果对比,二者计算结果基本吻合,亦符合规范规定。
2.3 结果对比
采用时程分析法与反应谱法计算得到的各层层间位移角如图10、11。
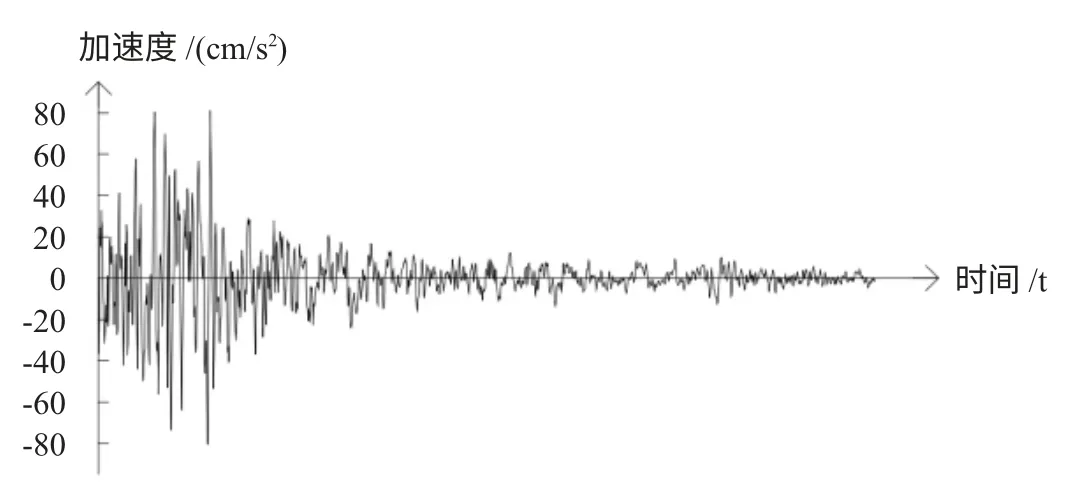
图6 天然波SAN FERNANDO 的X 向波形曲线

图7 天然波SAN FERNANDO 的Y 向波形曲线
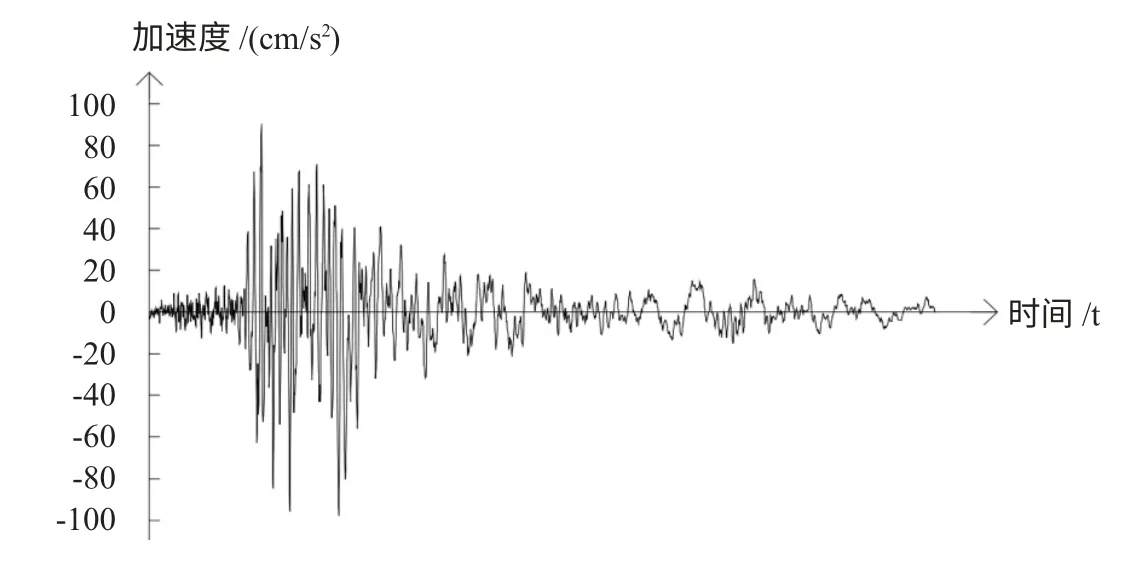
图8 天然波LYTLE CREEK 的X 向波形曲线
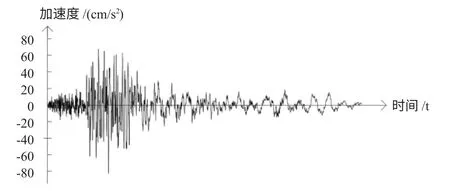
图9 天然波LYTLE CREEK 的Y 向波形曲线

表6 结构塑性铰的设置
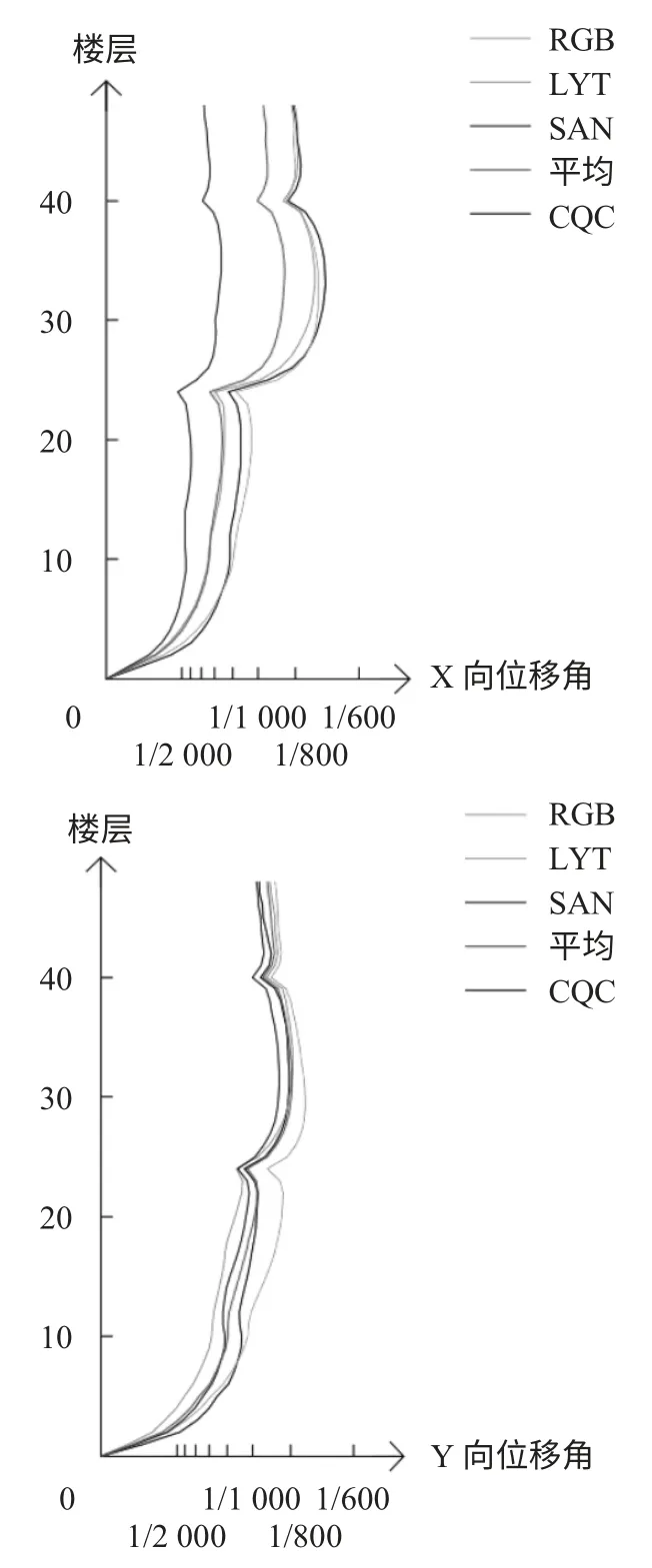
图10 弹性时程分析法与振型分解反应谱法X 向与Y 向层间位移角对比
由图中数据可以看出,对于X 向的层间位移角,弹性时程分析法计算的平均值小于反应谱法的结果;对于Y 向,从22 层开始,弹性时程分析法的平均值大于反应谱法的结果,但幅度较小(最大值为5.53%,47 层)。对于基底剪力,弹性时程分析法的平均值小于反应谱法,但上部有些楼层的层间剪力,弹性时程分析法的平均值大于反应谱法的结果,主要是47、48 层的X 向和20~34 层的Y 向,但幅值很小(仅0.2%~3.7%),所以在设计阶段,对于这些楼层的层间剪力,按弹性时程分析法的结果取用。
3 大震下静力弹塑性变形分析
3.1 参数设置
由于本结构的高度超过规范规定的限值较多,并且从25 层起,X 方向由于结构立面收进,造成结构竖向刚度变化较大。为了控制结构的竖向刚度和位移,在相应位置设置了伸臂桁架。因此,采用空间结构模型进行罕遇地震下的弹塑性变形分析,以准确反映结构在大震下的弹塑性变形性能和屈服机制,分析采用ETABS 程序进行。
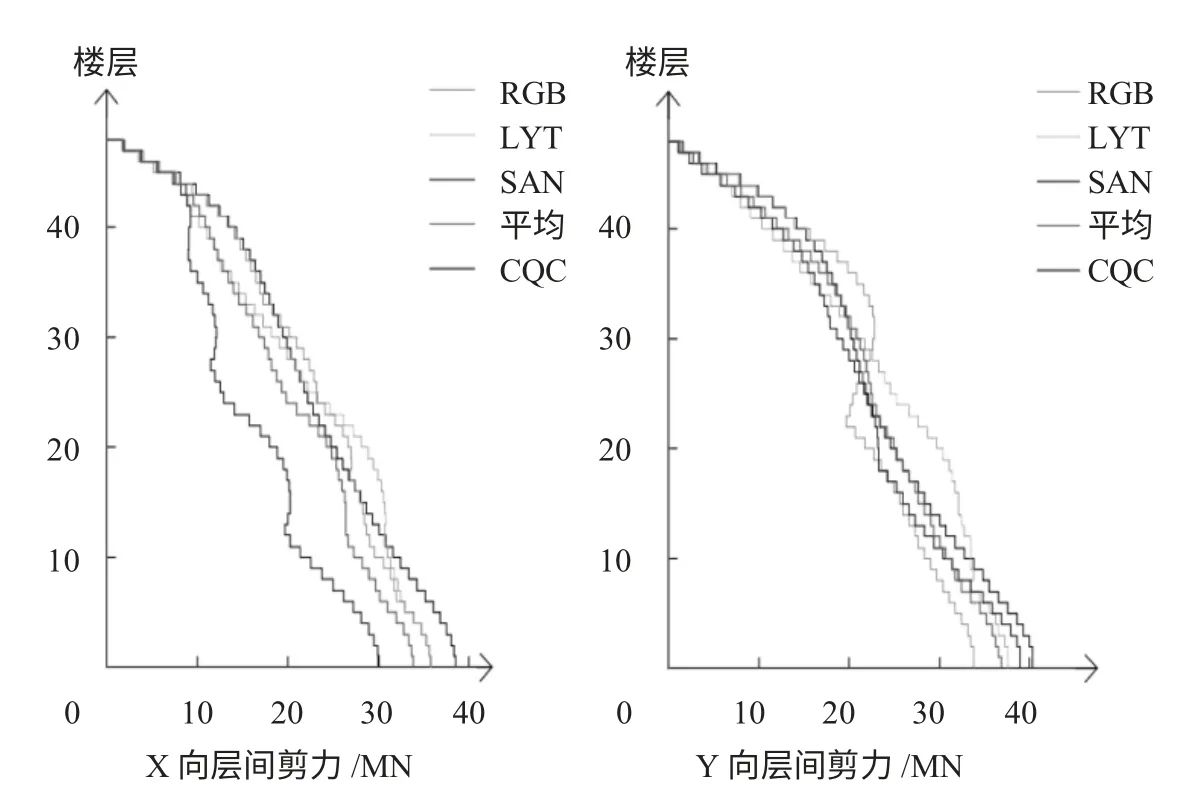
图11 弹性时程分析法与振型分解反应谱法X 向与Y 向层间剪力对比
3.1.1 塑性铰的设置
3.1.2 侧向加载模式
侧向荷载的分布方式,应该既能反映出地震作用下结构各层惯性力的分布特征,又能使所求的位移真实地反映地震作用下结构的位移状况[3]。因此,本工程采用按照结构的主振型分布方式进行侧向加载。即模型中的各个节点的力与该振型模态位移,模态角速度的平方以及从属此节点质量的乘积成比例,并在模态位移方向上作用。
根据整体结构在罕见地震作用下的弹性振型分解反应谱法的计算结果,机构的第一阶振型X 向平动质量参与系数为41%、Y 向平动质量参与系数为22%;第二阶振型X 向平动质量参与系数为63%、Y 向平动质量参与系数为64%。由此可认为,结构的地震响应以第二阶振型为主,而第二阶振型以平动为主,并包括一定的扭转效应。
弹塑性静力分析时,地震惯性力的大小是按照振型分布的。因此,结构在平面外会承受很大的扭转效应。对该结构而言,按第二阶振型侧向力分布进行分析,不仅能够反映结构的抗侧性能,也能够较准确地模拟结构在平面外的受力情况。
3.1.3 ETABS 中弹塑性工况参数
在ETABS 中,弹塑性计算过程分为两个工况,工况1 为在结构上施加竖向荷载,通常就是结构的1倍恒荷载+0.5 倍活荷载,加载监控目标为达到预定荷载;工况2 为在工况1 的基础上施加水平推覆荷载,加载监控目标为顶层位移达到结构总高度的1/50。
构件塑性铰的卸载方法选取“卸载整个结构”,这种方法效率最高,迭代计算参数根据多次计算得出经验,取最小保存步数为20 步,最多空步数取为50,最大总步数取为500,最多迭代次数取为20,这样设置可满足“卸载整个结构”对空步数的要求,同时可以使得计算时间大幅度减少。
3.2 能力谱法
ETABS 中性能平衡点的确定采用了ATC40 中的方法:性能平衡点是能力谱与一簇变化阻尼的需求谱之间交点中两种频谱的阻尼比相同的点。它的确定需要通过迭代完成,将弹塑性计算得到的力-位移关系和罕见地震下的反应谱分别转换为能力谱和需求谱,并绘在同一坐标系中[4]。
随着能力谱的原点割线斜率的减小,结构受到损坏,结构阻尼增大,相应的在该阻尼水平下需求谱响应减小,如下图,能力谱达到1 点后,结构显示出塑性性能,结构的刚度减小,周期增大,结构的阻尼比也有所增大,阻尼的加大引起需求谱的降低,当能力谱原点割线与相应阻尼需求谱交点位于能力谱上(图12 中4 点)时,该交点即为性能平衡点,由点2 至点4 的曲线反映了迭代的过程,如果这样的交点不存在,即表明结构难以抵御地震作用,将会倒塌。
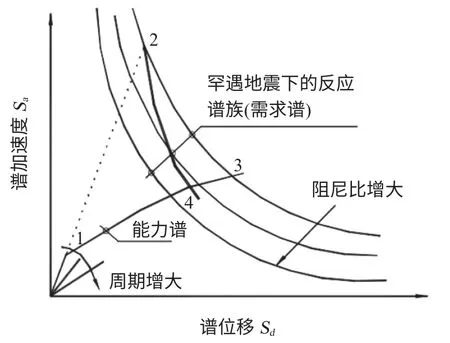
图12 性能平衡点迭代过程曲线图
ETABS 中内嵌了ATC40 的反应谱,用于性能平衡点的迭代计算。中国规范与ATC40 的反应谱的函数形式不同,可近似采用下列公式,将中国规范的反应谱用ATC40 反应谱等效。

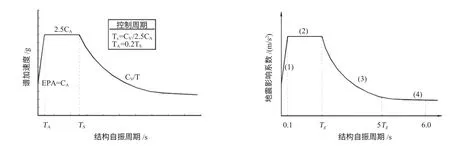
图13 ATC40 反应谱曲线与中国规范反应谱曲线对比图
式中:αmax为中国规范中的水平地震影响系数最大值,Tg为场地特征周期,CV、CA为ATC40 中在描绘谱加速度-谱位移曲线时所用的地震参数,其中CA为与地震加速度峰值成正比例的参数,CV是和阻尼相关联的参数。
从图14~16 可得,在结构弹塑性分析中,随着地震作用的增大,层间位移角较大的楼层(第31、32、33 层)首先出现塑性铰,其部位在与框架柱相连的梁端,并逐渐向上、下部楼层发展,极限状态下,部分梁端及大部分支撑均有塑性铰。结构的塑性铰主要出现在结构的框架梁及支撑上,说明支撑对结构的刚度贡献很大,同时也是结构耗能的主要构件。同时,在整个分析过程中塑性铰均出现在支撑和梁端,墙和柱均不出现屈服状态,说明本结构体系能够很好地满足“强柱弱梁”这一抗震的原则要求。

图14 结构模型

图15 X 向塑性铰分布情况

图16 Y 向塑性铰分布情况
在罕遇地震作用下,结构X 方向的最大层间位移角为1/163,Y 方向的最大层间位移角为1/175,均小于1/100 的规范限值,即结构满足“大震不倒”的抗震设防标准。

图17 X 向基底剪力与监测位移(N,mm)
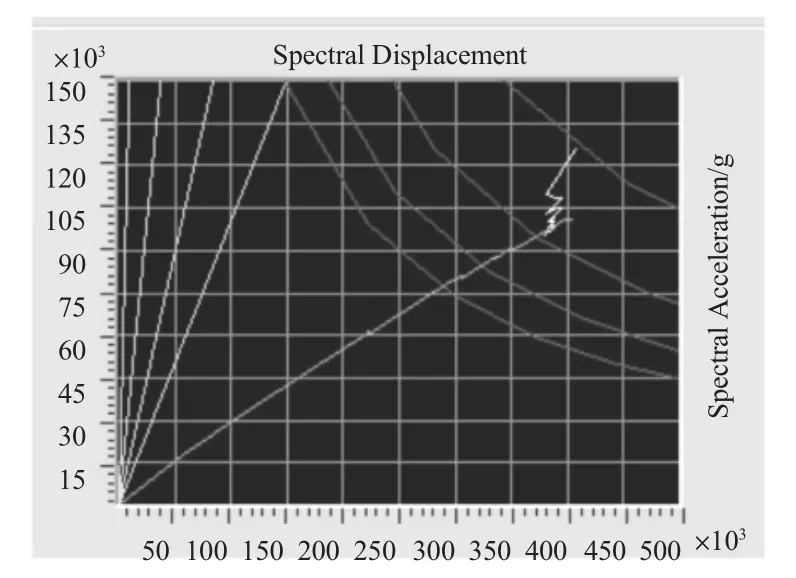
图18 X 向能力谱与需求谱曲线
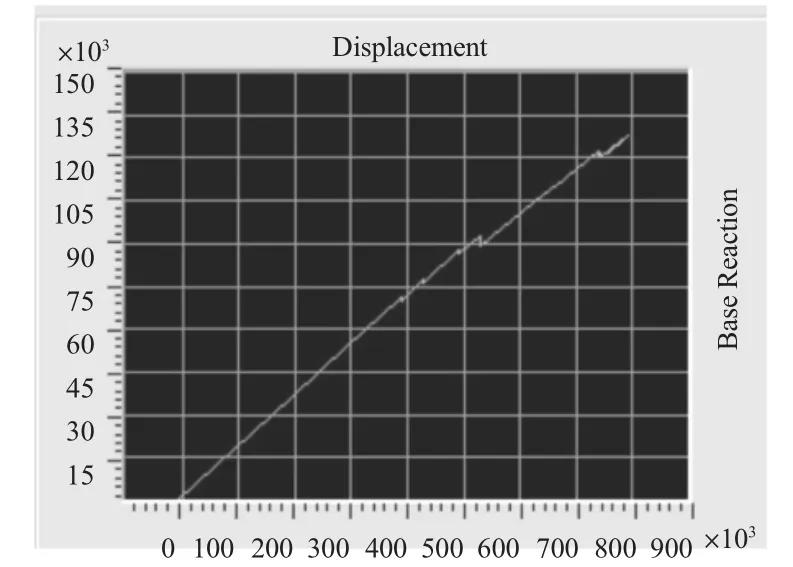
图19 Y 向基底剪力与监测位移(N,mm)
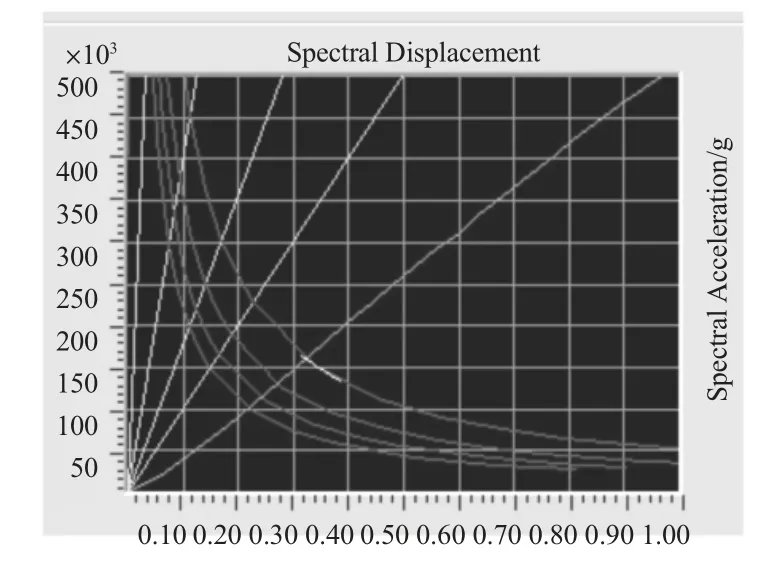
图20 Y 向能力谱与需求谱曲线
4 性能目标验算
对结构受力的关键部位及水平和竖向的薄弱部位进行截面验算:
4.1 底部加强区和25~26 层的筒体抗震墙,按“中震不屈服”进行抗弯设计验算
中震不屈服计算时,地震影响系数按小震时的2.812 倍取值,为0.45;荷载分项系数取1.0,保留各自的组合系数;构件的内力调整系数与承载力抗震调整系数均为1.0;材料强度采用标准强度。
通过验算,局部墙肢,主要是300 mm 厚薄墙存在计算超筋,且底部加强区出现的数量较25~26 层的筒体抗震墙多,但超筋的幅度不大,通过增大墙肢边缘约束构件的尺寸使其满足配筋要求。
4.2 底部加强区和25-26 层的筒体抗震墙,按“中震弹性”进行抗剪设计验算
中震弹性计算时,地震影响系数按小震的2.812倍取值,为0.45;荷载分项系数和各自的组合系数均保留;构件的内力调整系数为1.0;承载力抗震调整系数按规范取值;材料强度采用设计强度。
通过验算,中震条件下全楼墙肢验算中发现有569 片墙肢出现抗剪验算不满足,但均未出现在目标楼层,底部加强区和25~26 层的筒体抗震墙的全部墙肢均满足“中震弹性”的要求。
4.3 底层长、短柱分别承担全部的底层框架剪力验算
根据计算结果,基底剪力分别为38 516.57 kN(X 向)和40 385.12 kN(Y 向),框架的计算剪力为4 481.82 kN(X 向)和5 462.98 kN(Y 向),按照框架内力调整方法,取基底剪力的20%和框架计算剪力的1.5 倍两者的较大值,为8 194.47 kN,由全部的长柱和全部的短柱各自承担。
由于长柱的数量(6 根)比短柱(12 根)少,但截面相同,故可以仅验算长柱,调整后的柱内力为8 194.47/6=1 365.75 kN,柱截面为1 500×1 500×50×50 矩形钢管,内灌C60 混凝土,根据《矩形钢管混凝土结构技术规程CECS159—2004》[5],柱剪力可假定由钢管管壁承受,可得柱的抗剪承载力设计值为21 700 kN,远大于调整后的柱内力。
4.4 2 层大开洞楼板的验算
由于2 层楼板开有大洞口,局部楼板缺失面积达到31.8%,为真实反映该层楼板的空间特性,防止其由于承担过多的水平剪力,在楼板的薄弱处较早地进入塑性变形甚至发生破坏,需要对此部位的楼板进行有限元应力分析。对分析中出现的薄弱范围的楼板采取加大板厚和加强配筋的处理方法。
分析采用中国建筑科学研究院的PMSAP(特殊多高层建筑结构分析与设计软件,ver05.04)程序进行,模型中将2 层楼板全部设置为弹性板6(程序真实计算楼板的平面内和平面外刚度)进行分析计算。
从计算结果可知,多遇地震作用下2 层楼板的最大主应力分别为0.897 MPa(X 向)和0.981 MPa(Y 向),均小于混凝土轴心抗拉强度标准值(C40,2.39 MPa),可知在多遇地震条件下,楼板不会开裂,同时设计中将根据中震的水平地震影响系数与小震的水平地震影响系数的比值,将楼板应力放大2.8 倍进行配筋设计,保证在中震下楼板不屈服。
5 结语
本工程属于超高层建筑,由于在结构设计中采用了较为合理的结构布置,并在相应楼层设置伸臂桁架,同时加强楼板开大洞后形成的薄弱部位,使得整个结构具有良好的抗震性能,满足“强柱弱梁”这一抗震设计的基本要求,并达到了规范所要求的“小震不坏、中震可修、大震不倒”的三水准二阶段的设防目标,主要的计算结构满足现行规范和规程要求。
[1]JGJ3—2010,高层建筑混凝土结构技术规程[S].
[2]GB50011—2010,建筑抗震设计规范[S].
[3]熊向阳,戚震华.侧向荷载分布方式对静力弹塑性分析结果的影响[J].建筑科学,2001,17(5):8-13.
[4]王力,李红玲.静力弹塑性设计方法(pushover)的原理和改进[J].山西建筑,2013,17(29):8-9.
[5]CECS159—2004,矩形钢管混凝土结构技术规程[S].

