基于边光滑有限元方法的三角形单元在复合材料反对称铺设角层合板的自由振动分析中的应用
李 明,李 宁,李 诤,李 威
(1.海军驻渤船重工军代表室,辽宁 葫芦岛125004;2.华中科技大学 船舶与海洋工程学院,武汉430074)
目前,用于复合材料层合板分析的有限元单元主要基于以下三个理论:①经典层合板理论;②一阶剪切变形理论;③高阶剪切变形理论。有限元方法作为重要的数值方法被广泛应用,其中三角形单元以其方便的前处理和对复杂几何形状的适应性,深受研究者的喜爱。然而,有限元三角形单元的发展深受精度和稳定性低的制约。应变光滑技术是在节点积分无网格方法中为得到稳定解而提出来的[1],很快被应用到自然单元。针对有限元方法(FEM)“过刚”的问题[2-4],有研究将标准有限元方法和应变光滑技术结合起来提出的基于单元光滑的有限元方法(SFEM)和基于节点光滑的有限元方法edge-based smoothed finite element method(NSFEM)。与FEM“过刚”的特性相反,NS-FEM表现出“过柔”的问题,而过柔的模型也将会导致结果的不稳定。基于边光滑的有限元方法用于计算平面问题,表现出较好的性能[5]。本研究基于Mindlin一阶剪切变形理论,应用光滑有限元方法对复合材料层合板的自由振动进行分析。
1 光滑域的构造
在光滑有限元方法中,离散域也是基于普通三角形单元。假设问题域Ω离散为N个三角形单元,问题域,这些单元网格共有Nn个节点和Ne条边。将每条边的两个端点和这条边相邻的两个三角形单元的中心相连接,这样就在三角形单元的基础上形成了Ns个基于边的光滑域,问题域在这种情况下光滑域的数目与普通三角形单元边的数目相等,即Ne=Ns,见图1。
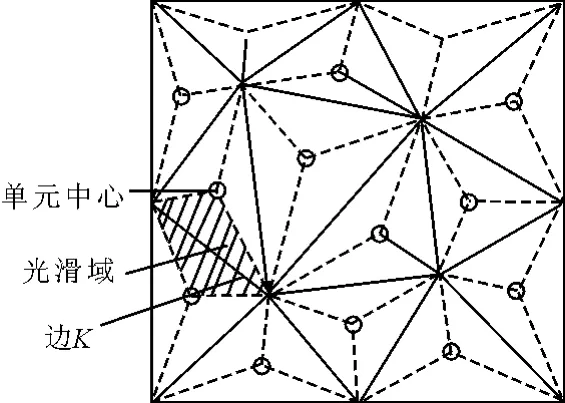
图1 三角形单元和基于边的光滑域
2 有限元模型
考虑一块固定厚度为h的层合板,由一定数目的铺设角为θ和-θ的各向异性等厚薄板交替铺设组成,每层板的材料均为正交各向异性体。坐标系的原点在层合板的中面,z轴垂直于板中面,见图2。

图2 反对称层合板示意
根据Mindlin假设,单元内任意一点的位移可表示为
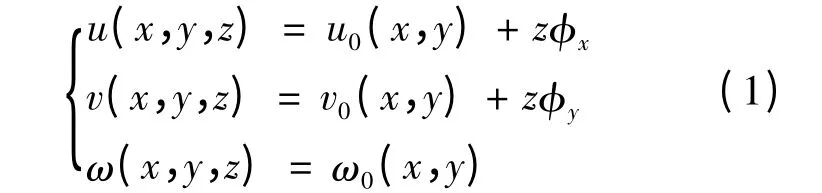
式中:u0、v0、ω0——中面上任一点的位移;
φx、φy——板变形后横截面绕坐标轴的转角。
线弹性位移应变关系为

对于正交各向异性体,每一层在(x,y)平面内的应力-应变关系为
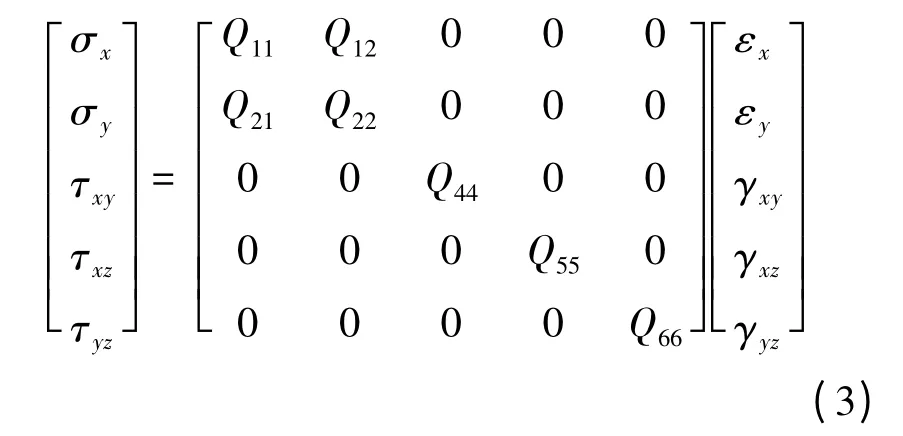
式(3)决定了层压板各层的弹性矩阵D,它和复合材料纤维铺设角θ有关,并且各层是不一样的,具体见文献[6]。
在每个铺层内沿z方向对各应力分量进行积分,式(2)、(3)用合力和位移的形式可表达为

式中:

刚度系数Qij取决于该层的材料特性和铺设角。参数k0为剪切修正系数。对于反对称层合板,系数A16,A26,B11,B12,B22,D16和D26等于零。
根据Hamilton原理,不考虑阻尼,可得层合板自由振动的有限元控制方程:
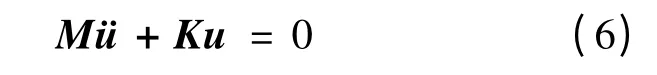
式中:M——结构的系统质量矩阵;
K——结构的系统刚度矩阵;
u——系统的位移矢量。
单元的刚度矩阵:
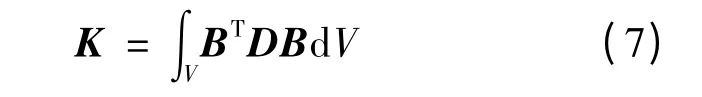
单元的质量矩阵:

式中:B——应变位移矩阵;
D——弹性矩阵;
N——形函数矩阵;
R——质量密度阵。

对第k层材料有

3 刚度矩阵光滑处理
在光滑有限元方法中,光滑刚度矩阵为

对于线性三角形单元网格,光滑应变位移矩阵¯B可以由式(12)求得:

Aej———边k周围第j个单元的面积;
Bej———边k周围第j个单元的应变位移矩阵;
Ask———边k所在光滑域的面积,对于三角形单元:

4 数值结果与讨论
为了验证光滑有限元方法的数值精度,下面分析反对称角铺设复合材料层合板的自由振动问题。四边简支矩形复合材料层合板,无量纲材料参数如下。
材料一:E1/E2=40,G12/E2=0.6,G13/E2=G23/E2=0.5,υ12=0.25;
材料二:E1/E2=25,G12/E2=0.5,G13/E2=G23/E2=0.2,υ12=0.25。
层合板无量纲一的量固有频率

式中:ω——圆频率;
a——层合板长;
h——板厚。
在同样的材料,面内位移,铺设角和网格划分等条件下用有限元方法和光滑有限元方法的计算结果见表1。层压板材料的物理参数为:a/h=10,a/b=1,四层反对称铺设,例如45°/-45°/45°/-45°。用21×21节点3DOF的FEM结果作为参考值,将FEM和ES-FEM的计算结果与其进行对照,可以看出,在相同的材料、节点划分、位移矢量和铺设角条件下,与FEM相比,ES-FEM的数值结果更精确。很显然,在0°~45°范围内,层压板自由振动的固有频率会随着铺设角的增大而增大,而随着铺设角的增长,固有频率增长的速度会放缓(铺设角为90°-θ的结果等于铺设角为θ的结果)。三自由度(3DOF)解是通过抑制面内位移(u,v)得到的。由表1的结果来看,在节点数比较少时,3DOF解更好一些,随着节点越来越密集,ES-FEM的5DOF解呈现出更好的收敛性。但无论是3DOF还是5DOF,ES-FEM都可以得到比FEM更好的结果。

表1 层压板面内位移、纤维铺设角、有限元网格对四边简支方板无量纲频率的影响
层压板铺设角和铺设层数对其无量纲基频的影响见表2。层压板材料的物理参数为:a/h=10,a/b=1,各铺层间的铺设情况为θ/-θ/θ/…/-θ。表中显示,层压板自由振动的基频会随着铺设层数的增加而增长,而随着铺设层数的增加,基频的增长会表现出越来越慢的趋势。两种方法的结果见表2。
5 结束语
本文采用边光滑有限元方法对复合材料层合板的自由振动进行分析,简单讨论了各参数对自由振动固有频率的影响,并将结果与标准有限元方法进行对比,结果表明:边光滑有限元方法改善了标准有限元方法模型过刚的问题,在同样的计算条件下结果更为精确,收敛性更好,是一种比较理想的数值计算方法。在接下来的工作中,将在以下几个方面开展进一步的研究和讨论。
1)针对更复杂的单元,例如多边形单元和体单元,验证光滑有限元方法的可靠性。
2)复杂边界和任意纤维铺设层条件下层合板的振动分析。
3)光滑有限元方法在夹层板振动和声辐射研究中的应用。

表2 层压板纤维铺设角、铺设层数对四边简支方板无量纲频率的影响
[1]CHEN JS,WU CT,YOON S,et al.A stabilized conforming nodal integration for Galerkin mesh-free methods[J].International Journal For Numerical methods in Engineering,2001(50):435-466.
[2]LIU G R,NGUYEN T T,DAI K Y,et al.Theoretical aspects of the smoothed finite element method(SFEM)[J].International Journal for Numerical Methods in Engineering,2007,71(8):902-930.
[3]LIU G R,DAI K Y,NGUYEN T T,et al.A smoothed finite element method for mechanics problems[J].Computational Mechanics,2007,39(6):859-877.
[4]LIU G R.A generalized gradient smoothing technique and smoothed bilinear form for Galerkin formulation of a wide class of computational methods[J].International Journal Of Computational Methods,2008,5(2):199-236.
[5]LIU G R,DAI K Y,NGUYEN T T.An edge-based smoothed finite element method(ES-FEM)for static,free and forced vibration analysis of solids[J].Journal of Sound and Vibration,2009(320):1100-1130.
[6]张少实,庄 茁.复合材料与粘弹性力学[M].北京:机械工业出版社,2005.

