信息快速插入与搜索算法研究

沈春元，张晓峰，李华君

(1.海军驻南京地区雷达系统军事代表室，南京 210003;2.中国船舶重工集团公司第七二四研究所，南京 210003)

0 引言

随着计算机的不断升级，关于信息的插入大多数采用的是遍历方式，在通常情况下很符合条件，其原理为:

(1）在信息库中查找是否有相同标识的信息，如果有转到(3），否则转到(2）;

(2）查找是否有空闲的位置，如果有转到(3），否则转到(4）;

(3）更新数据信息;

(4）满信息后，采用处理方式。

此算法的时间复杂度为O(2n）。在实际处理过程中，信息量越来越大，在一些强实时情况下，采用上述的算法很难达到要求。

本文提出的快速插入与搜索算法(Quick Insert and Search Algorithm，简写QISA）QISA算法主要包括快速插入算法(QIA）和快速搜索算法(QSA）。

1 快速插入算法

本文提出的快速插入算法(见图1），主要是基于双索引之上实时变化索引关系，快速达到空闲位置，其时间复杂度为O(1）。

图1中，索引表A 存放索引表B的位置信息，索引表B 存放索引表A 对应的位置信息，指针p为读指针指向当时可以写的位置，指针q为写指针指向索引表A中所要修改的位置。

图1 快速插入算法

图2 算法关系图

算法流程如下:

(1）初始化p和q 指向索引表A中的A1的位置，索引表A与索引表B 一一对应，如图1(b）所示;

(2）有信息输入时，直接索引到p所指定的位置，对应的索引表B中的信息为B［p］;

(3）第3个信息需要删除时(图2(a）），交换A［q］与A［Bi］中的位置信息，更新索引表A的值，其结果如图2(b）所示。

2 快速搜索算法

搜索算法实际上是根据初始条件和扩展规则构造一颗“解答树”并寻找符合目标状态的节点的过程。

图3 树形关系图

由图3所知，形成的一棵树为搜索树。初始状态对应着根节点，目标状态对应着目标节点，图中的实线则为我们需要寻找的路径。

本文采用的快速搜索算法(QSA）同样是基于树的关系之上，实时计算树信息，为之后搜索的信息提供必要条件。

信息不同构建搜索树的方式也会不同，本文处理的信息主要是关于点迹、航迹的信息。根据此特征选取一个标识，确定此标识为关键字，最后通过此标识来检索相关信息。其时间复杂度为O(L），其中L为标识的复杂度，例如用4 位的标识来确定关键字，那么L=4。

图4 标识分解树

由图4 可知，标识为“知419”，在树中表示为用实线箭头表示的成功路径。

算法流程如下:

(1）初始化树的根节点、标识有效信息;

(2）分解标识信息;

(3）查找搜索树，如果寻找到目标节点转到到(4），否则转到到(5）;

(4）更新目标节点信息;

(5）添加目标节点信息。

3 结果与分析

仿真环境配置:

CPU:Core i5系列、内存:4G、操作系统:Windows XP。

本文的仿真测试主要对20000 批内的批数进行抽样测试，测试结果如图5所示。

图5 测试结果图

由图5(a）所知，如果信息的批数在1000 批以内时，通用的算法优于本文的QISA，时间主要消耗在搜索树的构建上，其时间差也是控制在0.5 ms 以内。由图5(b）所知，当批数大于1000 批时，通用的算法时间会直线上升，QISA的耗时仍然是稳步上升;如果把批数提高到20000 批时，通用算法需要消耗约为477 ms，而QISA 则只需消耗约为20 ms的时间，如图5(c）所示。详细的数据对比结果如表1所示。

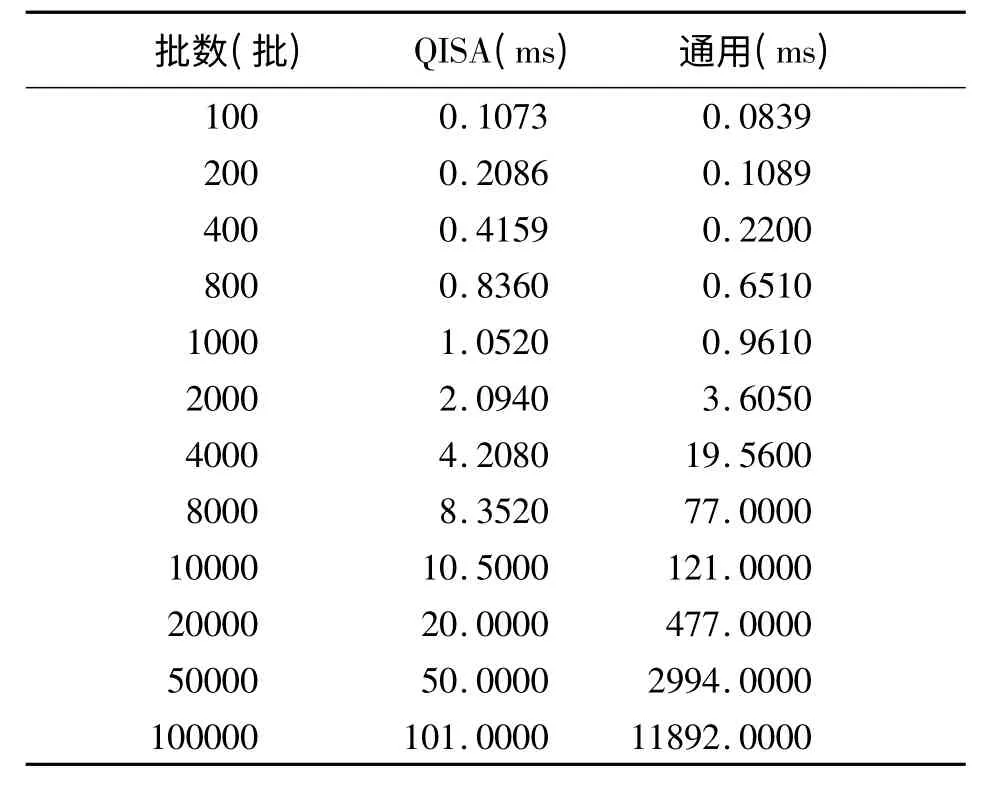
表1 QISA与通用结果对比

4 结束语

QISA 主要是采用了双索引技术，并构建搜索树的方式，实时为目标信息分配索引位置，减少了重复遍历搜索消耗的时间，提高了搜索速度。QISA的时间耗费主要在于对搜索树的建立、更新、删除等的操作，关系到系统内存的分配、更新、删除的操作，对QISA的更深入的研究可以扩展到内存优化的研究中。

［1］张水平.数据结构及算法分析［M］.西安:西北工业大学出版社，2003.

［2］夏定纯，徐涛，等.人工智能技术与方法［M］.武汉:华中科技大学出版社，2004.

［3］Thomas H.Cormen，Charles E.Leiserson，Ronald L.Rivest，Clifford Stein.Introduction to Algorithms［M］.3rd Edition.The MIT Press，2009.