离心泵蜗壳内压力脉动特性数值分析

刘厚林,杜 辉,董 亮,吴贤芳,刘东喜

(江苏大学流体机械工程技术研究中心,江苏镇江 212013)

离心泵蜗壳内压力脉动特性数值分析

刘厚林,杜 辉,董 亮,吴贤芳,刘东喜

(江苏大学流体机械工程技术研究中心,江苏镇江 212013)

为揭示离心泵蜗壳流道内的压力脉动变化规律,采用雷诺时均方法(RANS),对3种工况下的离心泵内部三维非定常湍流流场进行数值计算,分析同一蜗壳断面不同位置以及沿蜗壳周向不同点的压力脉动特性。结果表明:蜗壳流道内具有非常明显的压力脉动,在各种工况下压力脉动的主频均是叶片通过频率;同一蜗壳断面上的压力脉动从蜗壳底部到蜗壳背面先减小后增大,蜗壳底部监测点的高频脉动成分较多;沿蜗壳周向,随着圆周角的增大,压力脉动减弱,隔舌附近压力脉动幅度最大,且高频脉动成分明显增加。

离心泵;蜗壳隔舌;压力脉动;雷诺时均法;数值分析

离心泵的空间非对称结构使其内部流动呈现出复杂的非定常特性,这种特性使泵在产生静态压力分量的同时还会产生动态压力分量,也就是压力脉动[1]。

压力脉动在泵内是有害的,会引起泵系统及其设备的振动和噪声,严重时会损坏设备[2]。因而对蜗壳内部压力脉动特性进行研究有助于掌握泵内压力脉动发生和发展的特点,为泵的设计提供参考,从而提高泵和系统运行的稳定性。

获取压力脉动数据的最直接方法是进行试验测试,但是实际操作中受限于泵的体积等因素,实施起来具有很大的技术难度,且周期长,成本高[3]。计算流体动力学(CFD)技术的发展为压力脉动的研究提供了另外一种方法,其快速灵活的特点使其在压力脉动等泵的内部流动研究中得到越来越广泛的应用[4-7]。但以往的研究大多只针对叶片区域或者蜗壳背面附近点的压力脉动情况进行分析[8-12],对同一蜗壳断面上不同点的压力脉动情况以及压力脉动沿蜗壳周向的变化情况的研究则较少,进行这方面的研究能更充分地认识压力脉动在蜗壳内的分布,从而为减轻压力脉动提供指导。

本文选取商用CFD软件Ansys CFX,采用雷诺时均方法(RANS)计算了一台离心泵在3种工况下的三维非定常湍流流场,并对计算得到的压力脉动情况进行了分析。

1 数值计算模型

本文所用离心泵的参数如下:设计流量Qd= 0.0139m3/s,转速n=2900 r/min,比转数ns=99,叶轮外径D2=168 mm,叶轮出口宽度b2=10 mm,叶片出口安放角β2=31°,蜗壳基圆直径D3=180 mm,蜗壳进口宽度b3=20 mm,叶片数z=5。

2 数值计算方法

计算区域由进口延长段、叶轮、蜗壳、出口延长段4部分组成,如图1所示,采用网格划分软件ICEM划分得到网格总数为3550256个。

图1 计算区域及网格示意图

在进口延长段入口处设置速度进口,出口延长段设置自由出流出口,对于泵内转子部件和定子部件之间的交界面采用滑移网格进行处理,固壁采用无滑移壁面边界条件。

采用有限体积法对瞬态控制方程进行离散,利用CFX12.0全隐式耦合多网格线性求解器对所有变量整场联立求解,同时求解动量方程组和连续方程。在稳态求解阶段选取在离心泵数值计算中具有良好表现的标准k-ε湍流模型[12]进行计算,之后以此计算结果为非定常计算的初始场进行非定常求解。

在非定常计算时,将旋转水体与非旋转水体之间的交界面设置为瞬态动静转子(transient rotorstator)模式[13],这对于两部分水体间的动静干涉作用是至关重要的。

为了提高计算结果对内部流场的分辨率,选取叶轮每旋转1°为1个时间步长,所对应的时间为5.75×10-5s。这样每经过360个时间步为1个叶轮周期,共计算10个叶轮周期,取最后1个周期的数据进行处理,此时脉动已经稳定。

本研究所计算的3个工况点流量和设计流量之比Q/Qd分别为0.8、1.0和1.2。压力脉动监测点的设置如图2所示,其中P6、P6B和P6M是同一蜗壳断面上的点,分别位于蜗壳背面、蜗壳底部和蜗壳中间位置处。

图2 蜗壳区域压力脉动监测点设置示意图

3 计算结果与分析

3.1 外特性分析

根据计算得到的进出口总压力差以及轴功率可以得到泵在不同工况下的扬程和效率,如表1所示。从表1可见,扬程和效率计算值的总体趋势与试验值相同,扬程相对误差的最大值为5.05％,效率绝对误差的最大值为3.43％。可见本文所选取的计算方法较为准确地预测了该泵的外特性,从而为进一步的预测分析打下了基础。

表1 水泵外特性计算值和试验值的对比

3.2 压力脉动分析

3.2.1 不同工况下同一蜗壳断面上监测点压力脉动特性

为方便下面的阐述,这里定义压力脉动系数CP= (P-Pavg)/Pavg,其中P为静压,Pavg为静压平均值,该压力脉动系数是指压力脉动振幅占静压平均值的比例。同时对时间进行归一化处理,定义时间系数:Ct=(t-tb)/(te-tb),其中,tb为所选用叶轮周期开始时刻的时间,te为该叶轮周期结束时刻的时间。这样,该周期内压力脉动情况所对应的时间便可以用一个变化范围为0～1的无量纲系数来表示,以便于理解。

图3为不同工况下位于同一蜗壳断面上的3个点P6、P6B和P6M处的压力脉动时域特性。由图3可见,在各工况下,3个点的压力脉动均具有非常明显的周期性,呈现出非常规律的5个波峰和5个波谷,这正好与叶轮叶片数相同。但是3个点的压力脉动幅度不同。

由图3(a)可见,Q/Qd=0.8工况下,P6B处的脉动幅度最大,约为静压均值的2.5％;P6处的脉动幅度次之,约为静压均值的2％;P6M处的脉动幅度最小,为静压均值的0.8％。分析图3(b)和图3(c)可以得到与图3(a)相同的结论,即位于蜗壳底部的P6B脉动幅度最大;位于蜗壳背面的P6次之,但与P6B处脉动幅度差别不大;位于该蜗壳断面中间位置的P6M压力脉动幅度最小。这说明在同一蜗壳断面上,压力脉动幅度从蜗壳底部到蜗壳背面先减小后增大。理论上,这是因为在蜗壳底部和蜗壳背面,叶片和动静干涉作用的影响分别居于主导地位,而在蜗壳流道中间位置二者作用相对较弱的缘故。

通过快速傅里叶变换(FFT)得到上述各监测点在不同工况下的压力脉动频域特性,如图4所示。可以看出,在各工况下,同一蜗壳断面3个监测点的压力脉动频率均以叶片通过频率(242Hz)为主。其中,P6和P6M处的频率主要是叶片通过频率,高频成分很少。相比之下,P6B处的高频成分明显增多,可见,在叶轮的影响下,蜗壳底部监测点体现出了更为复杂的频率特性。

3.2.2 设计工况下蜗壳周向不同监测点的压力脉动特性

图5为设计工况下沿蜗壳背面周向各监测点的压力脉动时域特性。由图5可见,沿蜗壳周向各点的压力脉动均呈现出明显的周期性,具有5个波峰和5个波谷。但各监测点压力脉动的幅度不同,其中以正对隔舌处的P2点脉动幅度最大,约为静压均值的11.5％;P1和P3分别位于P2两侧,脉动幅度也较大,分别为静压均值的10.3％和8.7％。P4、P5、P7和P8处的压力脉动幅度分别为静压均值的5％、2.57％、0.9％和0.4％,均明显小于隔舌附近监测点的脉动幅度。可见沿蜗壳周向,隔舌附近监测点压力脉动幅度最大,这主要是因为叶轮与蜗壳的动静干涉作用在此处最为强烈;随着圆周角的增大,叶轮与蜗壳背面之间距离增大,叶轮与蜗壳的动静干涉作用减弱,脉动幅度逐渐减小。

图6是设计工况下沿蜗壳周向各点的压力脉动频域特性。由图6可知,蜗壳周向各点的压力脉动主频均在叶片通过频率处。隔舌附近3个点的脉动幅值均较大,且高频脉动成分较多;随着圆周角的增大,各监测点到隔舌的距离增加,压力脉动幅值减小,叶片通过频率逐渐居于统治地位,高频脉动明显减少。可见,隔舌对离心泵压力脉动频域特性的影响显著。

图3 不同工况下同一蜗壳断面上监测点压力脉动时域

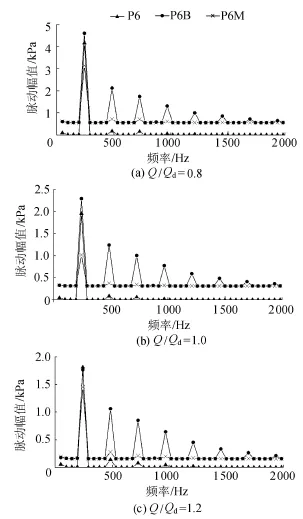
图4 不同工况下同一断面上监测点压力脉动频域

4 结 论

a.蜗壳流道内各监测点的压力脉动具有非常明显的周期性,且在各种工况下的主频均为叶片通过频率。

图5 设计工况下蜗壳周向不同监测点压力脉动时域

图6 设计工况下蜗壳周向不同监测点压力脉动频域

b.处于同一蜗壳断面不同位置的监测点的压力脉动幅度不同,从蜗壳底部向蜗壳背面先减小后增大,且位于蜗壳底部监测点的高频脉动成分较多。

c.沿蜗壳周向,隔舌附近监测点压力脉动幅度最大,频域特性也最为复杂,高频脉动成分十分明显;随着圆周角的增加,各监测点沿周向与隔舌距离变大,脉动幅值逐渐减小,叶片通过频率居于主导地位,高频脉动成分很少。

[1]朱荣生,苏保稳,杨爱玲,等.离心泵压力脉动特性分析[J].农业机械学报,2010,41(11):43-47.(ZHU Rongsheng,SU Baowen,YANG Ailing,et al.Numerical investigationofunsteadypressurefluctuationsin centrifugal pump[J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(11):43-47.(in Chinese))

[2]袁建平,付燕霞,刘阳,等.基于大涡模拟的离心泵蜗壳内压力脉动特性分析[J].排灌机械工程学报,2010,28 (4):311-314.(YUAN Jianping,FU Yanxia,LIU Yang, et al.Analysis on pressure fluctuation within volute of centrifugal pump based on large eddy simulation[J]. Journal of Drainage and Irrigation Machinery Engineering, 2010,28(4):311-314.(in Chinese))

[3]瞿丽霞,王福军,丛国辉,等.双吸离心泵叶片区压力脉动特性分析[J].农业机械学报,2011,42(9):79-84. (QU Lixia,WANG Fujun,CONG Guohui,et al.Pressure fluctuations of the impeller in a double-suction centrifugal pump[J].Journal of Drainage and Irrigation Machinery Engineering,2011,42(9):79-84.(in Chinese))

[4]BYSKOV R K,JACOBSEN C B,PEDERSEN N.Flow in a centrifugal pump impeller at design and off-design conditions:partⅡ:large eddy simulations[J].Journal of Fluids Engineering,2003,125(1):73-83.

[5]NAGAHARA T,INOUE Y,SATO T,et al.Investigation of the flow field in a multistage pump by using LES[C]// Proceeding of the ASME Fluids Engineering Division Summer Meeting.Houston:ASME,2005:1321-1329.

[6]朱荣生,胡自强,杨爱玲,等.双叶片泵内非定常流动的数值模拟[J].排灌机械工程学报,2011,29(1):26-30. (ZHU Rongsheng,HU Ziqiang,YANG Ailing,et al. Numerical investigation of unsteady pressure fluctuations in centrifugal pump[J].Journal of Drainage and Irrigation Machinery Engineering,2011,29(1):26-30.(in Chinese))[7]杨敏,闵思明,王福军.双蜗壳泵压力脉动特性及叶轮径向力数值模拟[J].农业机械学报,2009,40(11):83-88.(YANG Min,MIN Siming,WANG Fujun.Numerical simulation of pressure fluctuation and radical force in a double volute pump[J].Transactions of the Chinese Society for Agricultural Machinery,2009,40(11):83-88. (in Chinese))

[8]柴立平,潘兵辉,石海峡,等.高速部分流泵整机非定常流动数值模拟[J].排灌机械工程学报,2011,29(4): 303-306.(CHAI Liping,PAN Binghui,SHI Haixia,et al.Numerical simulation of unsteady flow in high-speed partial emission pump[J].Journal of Drainage and Irrigation Machinery Engineering,2011,29(4):303-306. (in Chinese))

[9]康伟,祝宝山,曹树良.离心泵螺旋形压水室内流场的大涡模拟[J].农业机械学报,2006,37(7):62-65. (KANG Wei,ZHU Baoshan,CAO Shuliang.Large Eddy Simulation of the flow through the spiral casing of a centrifugal pump[J].Transactions of the Chinese Society for Agricultural Machinery,2006,37(7):62-65.(in Chinese))

[10]刘厚林,任芸,谈明高,等.双流道泵内压力脉动的CFD计算及测试[J].排灌机械工程学报,2010,28(4):277-281.(LIU Houlin,REN Yun,TAN Minggao,et al.CFD calculation and test of pressure fluctuation in doublechannel pump[J].Journal of Drainage and Irrigation Machinery Engineering,2010,28(4):277-281.(in Chinese))

[11]王春林,易同祥,吴志旺,等.混流式核主泵非定常流场的压力脉动特性分析[J].动力工程,2009,29(11): 1036-1040.(WANGChunlin,YITongxiang,WU Zhiwang,et al.Analysis on pressure fluctuation of unsteady flow field in mixed-flow main coolant pump[J]. Journal of Power Engineering,2009,29(11):1036-1040. (in Chinese))

[12]耿少娟,聂超群,黄伟光,等.不同叶轮形式下离心泵整机非定常流场的数值研究[J].机械工程学报,2006,42 (5):27-31.(GENG Shaojuan,NIE Chaoqun,HUANG Weiguang,et.al.Numerical study of unsteady flow in centrifugal pump with different type of impellers[J]. Chinese Journal of Mechanical Engineering,2006,42 (5):27-31.(in Chinese))

[13]祝磊,袁寿其,袁建平,等.阶梯隔舌对离心泵压力脉动和径向力影响的数值模拟[J].农业机械学报,2010,41(增刊1):21-26.(ZHU lei,YUAN Shouqi,YUAN Jianping,etal.Numericalsimulationonpressure fluctuations and radial hydraulic forces in centrifugal pump with step-tongue[J].Transactions of the Chinese Society for Agricultural Machinery,2010,41(Sup1)21-26.(in Chinese))

Numerical analysis of pressure fluctuation in the volute of centrifugal pump

//LIU Houlin,DU Hui,DONG Liang, WU Xianfang,LIU Dongxi(Research Center of Fluid Machinery Engineering and Technology,Jiangsu University,Zhenjiang212013,China)

In order to reveal the variation laws of the pressure fluctuation in the volute of a centrifugal pump,the threedimensional unsteady flow fields in the centrifugal pump under three different conditions are numerically solved by means of the Reynolds-averaged Navier-Stokes method.The pressure fluctuations at different points of the same section of the volute and different points along the circumferential direction of the volute are analyzed.The results show that the pressure fluctuations in the volute are obvious.The dominant frequencies under three conditions are found to be the ones that the blades pass.The pressure fluctuations at the same section decrease first and then increase from the bottom to the rear of the volute,and high-frequency fluctuations at the monitoring points on the bottom of the volute are evident.Along the circumferential direction,with the increase of circular angles,the pressure fluctuations decrease.The amplitude of pressure fluctuations is the largest near the tongue where high-frequency fluctuations dramatically increase.

centrifugal pump;tongue;pressure fluctuation;Reynolds-averaged Navier-Stokes method;numerical analysis

10.3880/j.issn.10067647.2013.01.004

TV136+.2

A

10067647(2013)01001804

2012-04-25 编辑:周红梅)

国家自然科学基金(51179075,51079062);江苏省自然科学基金(BK2009006,BK2010346);江苏省成果转化资金专项(BA2010155)

刘厚林(1971—),男,江苏溧水人,研究员,博士,主要从事泵现代设计理论与方法研究。E-mail:liuhoulin@ujs.edu.cn