一类线性多乘积规划的分支定界算法

赵营峰,尹景本

（河南科技学院,河南新乡453003）

一类线性多乘积规划的分支定界算法

赵营峰,尹景本

（河南科技学院,河南新乡453003）

针对广泛应用于金融及经济等实际问题中的一类线性多乘积规划问题,提出一种分段线性化全局优化算法.首先将问题转化为等价问题,然后利用分段线性化技术得到问题目标函数和约束函数的线性下界,构造出等价问题的松弛线性规划,并从理论上证明了算法的收敛性.数值试验表明算法是有效可行的.

多乘积规划；分支定界；松弛线性规划

多乘积规划广泛应用于产品计划、任务管理、化学工程设计、交通运输和商业等很多领域[1-4].本文针对一类特殊的线性多乘积规划问题提出了一种新的分枝定界算法,该算法在理论上具有重要意义,很多数学规划是其特殊情形或者可以转化为多乘积规划[5-9].针对多乘积规划问题,首先利用恒等变形,建立了原问题的等价问题,然后对等价问题进行松弛得到松弛线性规划,通过对松弛线性规划的可行域的细分以及一系列线性规划的求解,不断更新上下界,并从理论上证明了算法收敛到原问题的全局最优解.

1 松弛线性规划

考虑如下线性多乘积规划问题

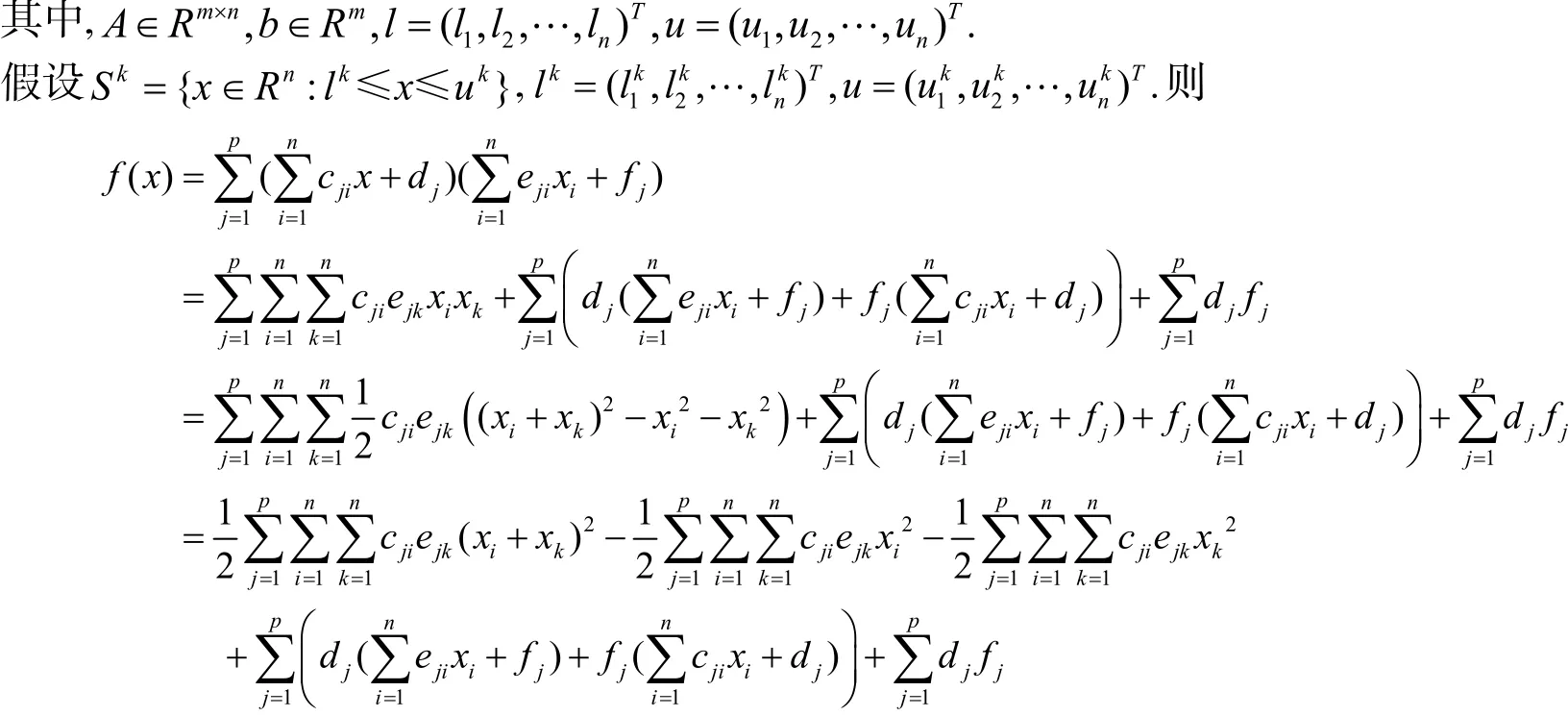
根据x2i在区间[li,ui]上的几何性质可知

且

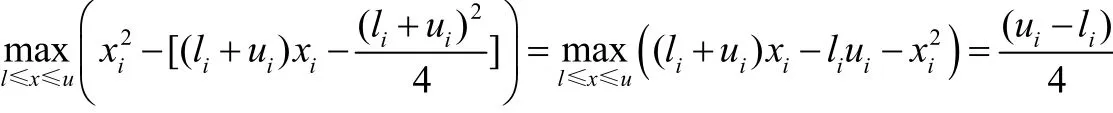
因而令

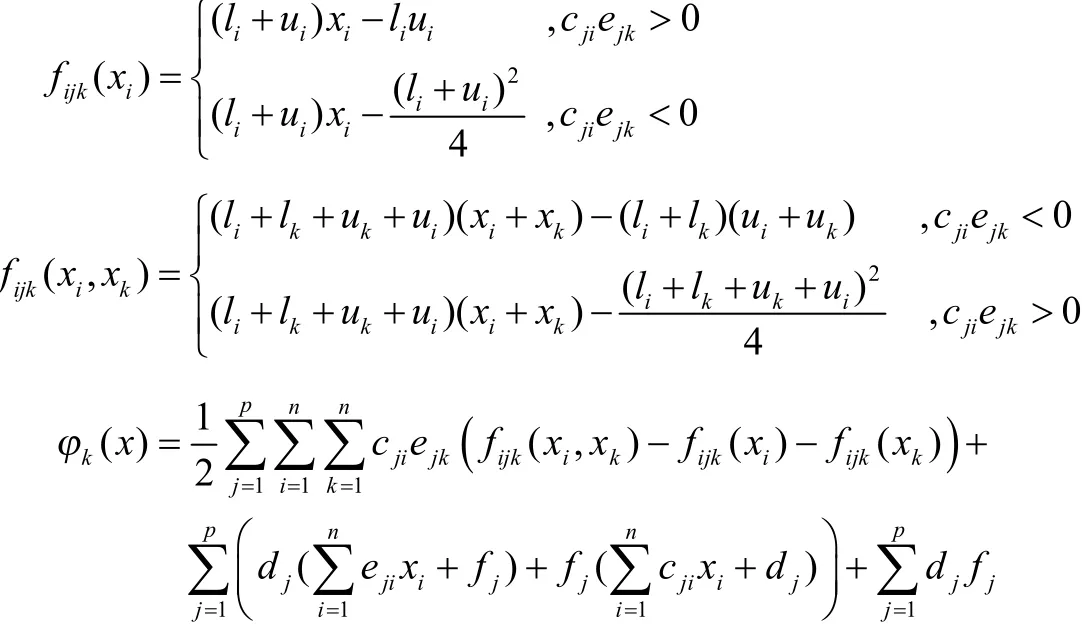
可得到问题（P）在Sk上的松弛线性规划

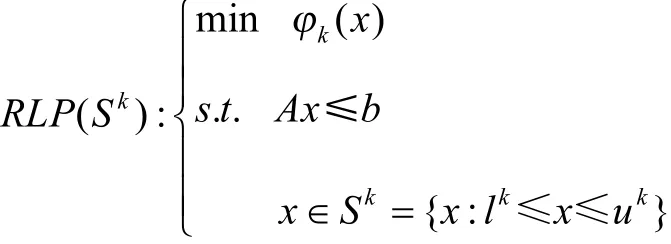
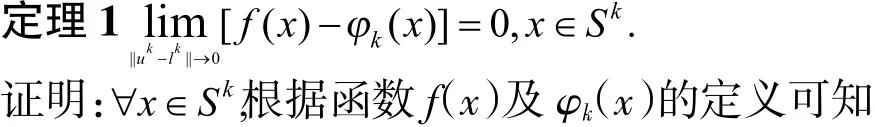
2 分支定界算法

下面给出分支定界算法,通过求解一系列松弛线性规RLP（Sk）,逐步改进原问题（P）的最优值的上界和下界,最终确定（P）的全局最优解：

步骤1.给定收敛参数ε＞0,可行点集F=Φ,置迭代次数k=1,上界uk=∞,活动节点,求Lk={Sk}解松弛线性规划RLP（Sk）,设其最优解和最优值分别为xk*和vk=φ（xk*）,令下界lk=vk,若xk*是原问题（P）的可行解,则令uk=f（xk*）,若uk-lk≤ε,算法停止,且xk*和vk=φ（xk*）就是原问题的全局最优解和最优值,否则执行步骤2.

步骤2.沿着垂直于Sk的最长边方向平均分割Sk为两部分设为S1k、S2k,然后分别求解RLP（Stk）,t=1,2.假设求得的最优解和最优值分别为xkt*和vk=φ（xkt*）,如果xkt*对原问题（P）可行,则令F=F∪{x（Stk）}, uk=min{uk,f（xkt*）}.

定理2若问题（P）的全局最优解存在,则算法或在有限步内求得问题（P）的全局最优解,或产生收敛到问题全局最优解的迭代序列{yk}.

证明：若算法在有限步内终止,则根据算法知算法终止时uk-lk=f（xk*）-φ（xk*）ε.设v为问题的全局最优值,因为xk*是问题的一个可行解,所以

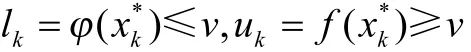
因此

命题成立.

如果算法产生一个无限迭代序列{yki},由于原问题的可行域是紧的,可设y*是它的一个聚点,则存在子序{yk}列收敛到y*.由算法知uk是单调递减有界序列,lk是单调递增有界序列,所以

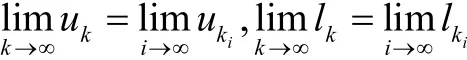
不妨设序列{yki}对应的序列对原问题是可行的.

由于

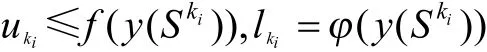
所以

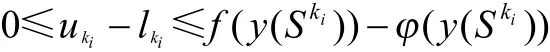
而举行的二分法是穷举的且f（x）和φ（x）都是连续函数,因而

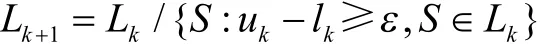
即

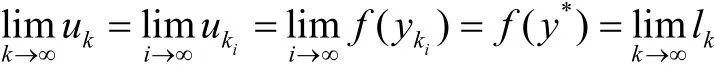
故y*是原问题的全局最优解.

3 数值实验

为了验证本文算法的可行性及有效性,采用Matlab编写程序,其中的线性规划采用单纯形方法求解,计算如下例题

经上机测试,算法仅经1次迭代即达到问题的全局最优解（2.0,8.0）.数值实验说明本算法是高效可行的.

4 小结

本文针对一类多乘积线性规划问题,提出了一种新的分支定界收算法,数值实验表明算法高效可行.

[1]Konno H,Yajima Y,Matsui T.Parametric simplex algorithms for solving a special class of nonconvexminimization problems[J]. JournalofGlobalOptimization,1991,1（1）：65-81.

[2]Benson H P,BogerGM.Outcome-space cutting-planealgorithm for linearmulti-plicative programming[J].JournalofOptimization Theory and Applications,2000,104（2）：301-322.

[3]CploantoniCS,Manes R P,Whinston A.Programming,profit rates and pricing decisions[J].The Accounting Review,1969,44（3）：467-481.

[4]Ellero A.The optimal levelsolutionsmethod[J].Journalof Information&Optimization Sciences,1996,17（2）：355-372.

[5]Konno H,Watanabe H.Bond portfolio optimization problems and their application to index tracking：a partial optimization approach[J].Journalof theOperations Research Society of Japan,1996,39（3）：285-306.

[6]Kuno T.A finite branch-and-bound algorithm for linear multiplicative programming[J].Computational Optimization and Application,2001,20（2）：119-135.

[7]Kuno T.Globally determining a minimun-aera rectangle enclosing the projection of a higer dinmensional[J].Operations Research Letters,1993,13（5）：295-303.

[8]Jiao H W,Guo Y R,Shen P P.Global optimization of generalized linear fractional programming with nonlinear constraints[J]. Applied Mathematicsand Computation,2006,183（2）：717-728.

[9]Ryoo H S,SahinidisNV.GlobalOptimization ofmultiplicative programs[J].JournalofGlobalOptimization,2003,26（4）：387-418.

（责任编辑：卢奇）

A global Optim ization Algorithm for a class of linear multip licative programm ing

Zhao Yingfeng,Yin jingben
（Henan InstituteofScienceand Technology,Xinxiang453003,China）

In this paper a piecewise linearization global Optimization Algorithm is proposed for the linear multiplicative programming,which has a lot of important applications in various areas such as financial optimization and economy plan．Firstly,the original program is transformed into the equivalent problems．Second,utilizing piecewise linearization technique,linear underestimates of the objective and constraint functions,linear relaxation programming for linearmultiplicative programming is established over a rectangle,and the proposed global optimization algorithm is proposed that can converge to the globally optimal solution．And finally the numerical experiments are given to illustrate that the proposed algorithm is effective and feasible．

multiplicative programming；branch and bound；linear relaxation programming

O221.1

A

1008-7516（2013）03-0086-04

10．3969/j．issn．1008-7516．2013．03．018

2013-04-23

河南省高等学校青年骨干教师资助计划（2010GGJS-140）；河南省教育厅自然科学研究项目（2010B110010）

赵营峰（1982-）,男,河南辉县人,讲师．主要从事最优化理论与算法研究．