非对称截面环状Kirchhoff弹性细杆的拓扑构型分析
张琪昌,赵 彬,王 炜
(1. 天津大学机械工程学院,天津 300072;2. 天津大学天津市非线性动力学与混沌控制重点实验室,天津 300072)
非对称截面环状Kirchhoff弹性细杆的拓扑构型分析
张琪昌1,2,赵 彬1,2,王 炜1,2
(1. 天津大学机械工程学院,天津 300072;2. 天津大学天津市非线性动力学与混沌控制重点实验室,天津 300072)
为了揭示非对称截面环状Kirchhoff弹性细杆受到外力(矩)作用时其拓扑状态的变化情况,引入了等效初始扭矩的概念,利用势能密度函数与哈密顿函数形式上的相似性,建立了其与系统哈密顿函数、初始自连接数之间的定量关系.以环状DNA分子为背景,对扭矩模型进行了非线性动力学分析,并利用解析方法中的待定固有频率法,分析了主要参数对扭矩模型稳定构型的影响.最后,利用等效刚度得到相应状态下曲率的表达式,为进一步认识和描述DNA环受到生物酶作用下的稳定构型提供了新的理论途径.
Kirchhoff;弹性细杆;环状DNA分子;待定固有频率法;非线性动力学;等效初始扭矩
关于环状弹性细杆的研究,目前所采用的模型是在Kirchhoff假设的基础上,将直杆两端的边界条件进行等效处理,从而衍生出环状形态的杆[1-4].Shi等[4]在弹性杆Kirchhoff方程基础上,以弹性杆的曲率和挠率为基本变量,建立了圆截面弹性杆的Schrödinger模型,并获得了其椭圆函数形式的近似解析解.刘延柱等[5-7]基于弹性杆非线性力学的经典理论,研究了以分子生物学为背景的弹性杆平衡和稳定性问题,发展了以欧拉角为坐标的参数理论体系,在静、动力学方面都获得了大量很有启示意义的结论.文献[8-9]中引入复刚度概念,推导出了非圆截面弹性杆的Schrödinger方程,并同样获得了其椭圆函数形式的近似解析解.王炜等[10]在考虑DNA弹性细杆截面非对称性特征的基础上,构造出复数形式的Kirchhoff系统,利用复变量力矩设解形式,并对Kirchhoff高维系统进行有效简化,得到了以外力矩轴向分量为单独变量的二阶常微分方程.
众所周知,DNA是由两条超长碱基链按一定顺序配对排列而成,由于细胞的空间约束性,现实中的DNA不存在直杆状态,DNA链必须在特定的外力及外力扭矩作用下发生缠绕、弯曲,形成超螺旋状态,基于此研究弹性杆拓扑构型及其发展演变,将有助于揭示其生物学本质.文献[1-2]中提出了一种基于能量最小原理与解析方法的判定方法,该方法可以判定环状杆构型的分岔现象.与数值方法中通常采用的Monta Carlo理论相比,在所得结果基本一致的前提下,定量分析不仅计算耗时短,而且还可以有效地反映拓扑参数之间的相互关系.正是基于上述考虑,作者提出了用连接数和缠绕数来描述弹性杆构型的新方法.
为深入分析外力(矩)作用对弹性杆构型的影响,本文首先引入了等效初始扭矩的概念,运用解析方法,充分分析了其对系统参数和扭矩模型参数的影响.再对文献[10]所提出的扭矩模型进行进一步探讨,结合非线性动力学待定固有频率法[11-12],求出了形式更为直观的近似解析解,利用等效刚度的概念,求出了弹性杆挠性线曲率的表达式.结合环状杆的边界条件,分析了不同力矩作用下杆的姿态特性变化,画出了相应状态下挠性线的实际效果图.
1 等效初始扭矩
任意一个初始扭率为0的环状弹性杆姿态均可由这样的形式得到:如图1所示,在一个挠性线初始扭率为0的非圆截面弹性杆上,设定点O为弧长原点(弧长s变化范围为0~L,L为杆长),在s=0和s=L处两截面分别施以大小相等、方向相反的等效初始扭矩对M30(沿弹性杆中心线切线方向)和主矢对F,使得杆在两端界面发生扭转的同时,保持两界面的距离始终为无限小,当达到既定的状态时,将两端重新粘结在一起,再次形成闭合的回环.非对称截面杆的截面如图2所示,其中Rxy和Rz分别表示垂直轴线上的长短半轴,且Rxy∶Rz≈1.
由于在这个过程中,主矢F的作用只限于控制s=0和s=L两截面之间的距离,使二者不至于分离太远,而扭矩M30才对该环状弹性杆输入有效能量.为保证首尾截面上同一挠性线的首尾端曲率以及曲率变化情况一致,初始扭矩M30的做功扭角必须满足φ=2nπ,n为正整数.在上述过程中,主矢F只是起到端面轴向固定作用,并没有能量输入,大小可以忽略.而初始扭矩M30在做功完成之后使弹性杆的首尾截面相对扭角为φ,杆自身作为传导两端力矩作用的载体,其内部的应力大小直接由M30决定.

图1 环状杆受到等效初始扭矩作用Fig.1 Effect of equivalent initial torque on ring rod

图2 非对称截面杆的截面(Rxy∶Rz≈1)Fig.2 Cross section of asymmetric elastic rod(Rxy∶Rz≈1)
综上所述,由于初始扭矩方向为沿截面法线方向,不具有其他方向的分量,且首尾截面没有发生相对位移和扭角,主矢F(包括其轴向分量F3)对系统的做功为0,可以将哈密顿函数H的定义式简化为

式中:A、B均为弹性杆抗弯刚度;C为抗扭刚度.由式(1)可以看出,此时等效初始扭矩M30的大小,决定了弹性杆再次闭合后封闭系统中的能量,据此,可以由M30对封闭环状杆的状态进行标定.
根据势能最小原理[5],弹性杆的实际平衡状态对应于总弹性势能的极小值,即总势能为0的状态,故有

式中:δE为总势能的一阶变分;Γ为势能密度函数.由于在忽略主矢F的前提下,势能密度函数Γ=H ,首尾端面相对虚角位移为δφ= φ.式(2)中第2个等号两边对弧长s求导,再考虑自连接数的定义,可知初始自连接数Lk0与M30的关系为

生物学上,DNA的扭转、剪切以及聚合等过程是由各种各样的酶来主导并实施的,例如DNA限制性内切酶、解旋酶、连接酶等,直接定量研究这些酶对DNA作用难度较大,而等效初始扭矩则可以在标定外界酶对DNA环的能量输入、预测DNA环在受一定扭矩后的稳定构型以及确定环状杆在某一状态下的数学模型等方面发挥重要作用.这也是本文研究环状弹性杆的拓扑参数进而开展动力学分析的前提条件.
2 动力学分析
非对称截面Kirchhoff杆的模型[10]为
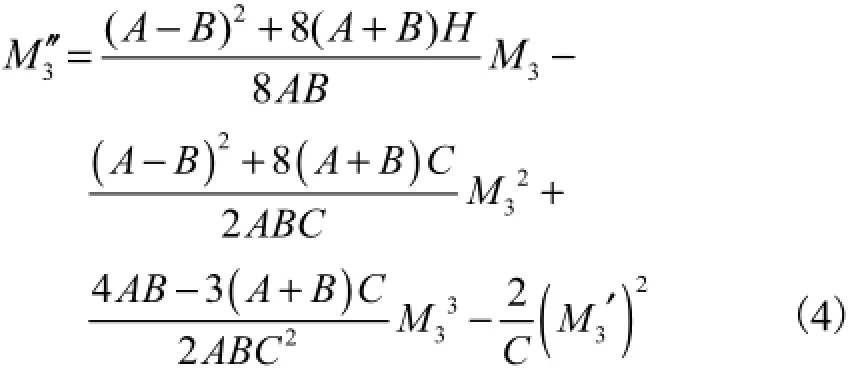
式中:M3为扭矩沿弧长s的分布函数;M′和M′′分别为M3对弧长s的一阶和二阶导数.
考虑实际参数意义可知,抗弯、抗扭刚度以及哈密顿函数值均为正值,所以式(4)中,等号右边关于扭矩M3一次方项的系数满足

该系数的相反数对应于常见振动微分方程中回复力的系数,即固有频率的平方,所以,该系统的平衡点可以在图3中得到定性的描述.利用稳定性理论可以判断出中间的坐标原点为鞍点,周围的轨线是不稳定的,而原点左右两边各分布一个中心点(R-,0)和(R+,0),其周围分布有稳定的轨线环1和环2,说明这两点附近的解是稳定的,而相应扭矩M3的周期变化幅值若超过一定范围,则表示其轨线已经达到甚至越过原点,形成跨度更大的环3和环4,扭矩M3出现零值,甚至跨越远点,出现负值,很显然这会使杆的姿态变得不稳定.
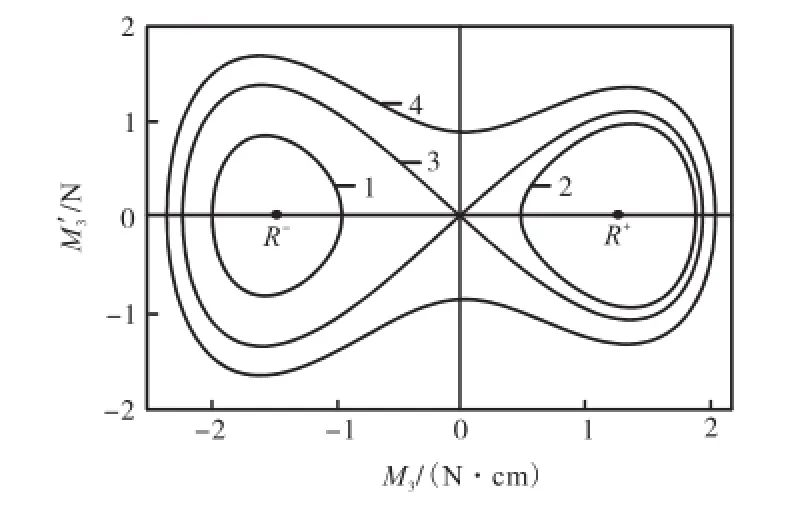
图3 扭矩模型的平衡点及相应的相图Fig.3 Equilibrium points and corresponding phase diagrams of torque model
根据实际意义,只有扭矩M3在正值区域内做周期运动时才是符合工程实际情况的,所以本文选择对右平衡点进行分析.由原振动方程可以知道,该平衡点(R+,0)的坐标其中
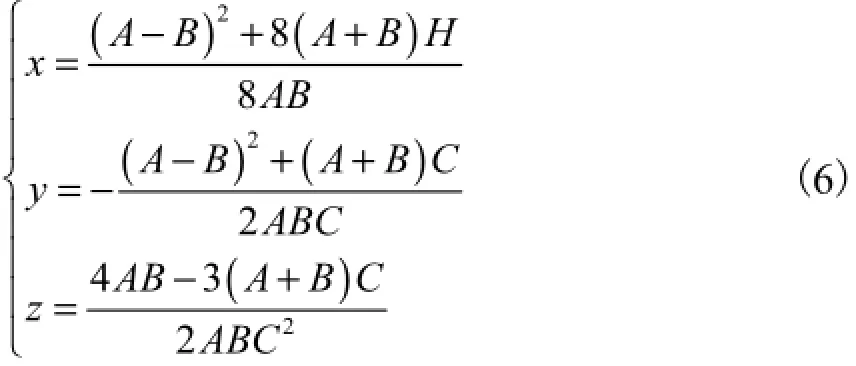
为便于计算和书写,设

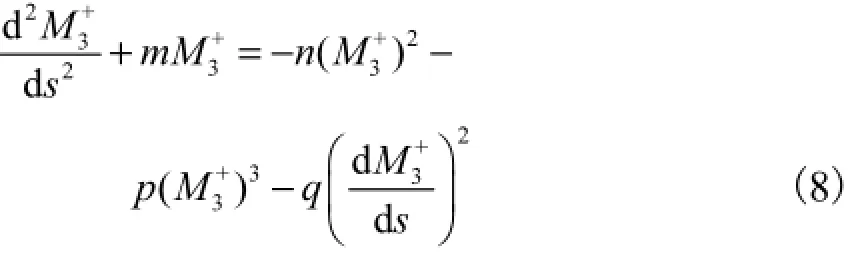
其中

利用待定固有频率法求得该振动系统的近似解析解为

式中:a为振幅;ω1为待定圆频率,二者关系为

幅值a随待定圆频率ω1的变化曲线如图4所示,可见a随ω1的增大而增大.环状杆的边界条件为

式中κ(s)为曲率沿弧长的分布函数.结合式(17)和式(3),可以得出

可见当杆长以及杆的材料特性不变时,环状弹性杆扭矩变化的圆频率与初始等效扭矩大小成正比关系.
综合式(13)~式(17),可以确定出扭矩的近似解析解,这意味着在运用解析方法的基础上,弹性杆稳定构型受各个参数变化的影响而发生的变化情况可以动态的形式得出.同时,由于该扭矩模型可进一步发展和完善,研究者根据模型参数情况,可以更加准确、清晰地判断其对杆构型的影响情况.
利用非对称截面等效刚度Beff的定义[10]可知

根据本构关系

可以得出

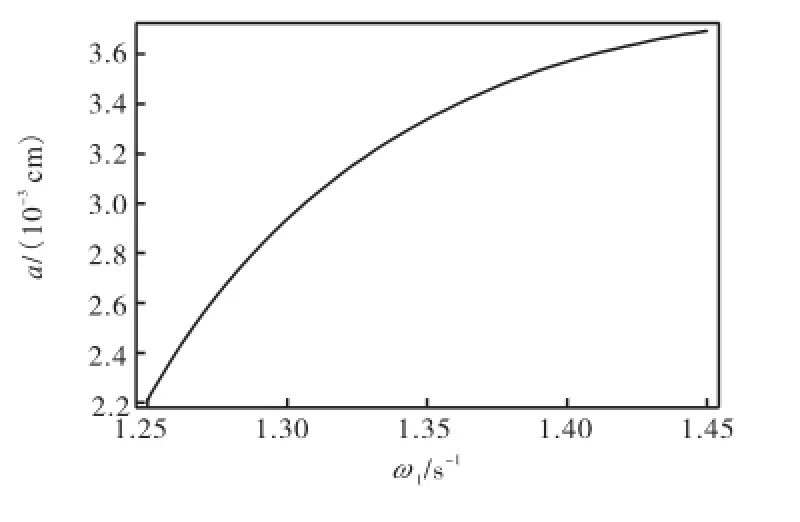
图4 幅值随待定圆频率的变化曲线Fig.4 The ω1-a curve
从而得到了非对称截面Kirchhoff杆挠性线曲率的表达式.上述讨论的右平衡点附近扭矩的周期变化区域始终为正,这也恰恰符合曲率平方的取值范围.
3 数值模拟
本节将以第2节得到的解析解为基础,带入具体数值,分析等效初始扭矩对环状杆稳定构型的影响.
对弹性杆模型的物理参数进行取值:抗弯刚度分别为A=0.13,erg·cm和B=0.12,erg·cm,抗扭刚度C=0.10,erg·cm,杆长L=20,cm,Rxy∶Rz=1.3∶1.2.将其代入式(1)~式(3)以及式(7)~式(17),并将坐标原点移至原始系统的原点处,即M3=3M++ R. 取M30=1.6π N·cm,相应自连接数0kL=4,可得

再将式(22)代入式(21),就可以进一步得到曲率平方的表达式为

取M30=2π N·cm,相应自连接数0kL=5,可以得到扭率近似解以及相应的挠性线曲率表达式为

利用Mathematica软件,分别画出M30=1.6π N·cm(0kL=4)和M30=2π N·cm(0kL=5)时扭矩变化相图和相应的随弧长变化的历程图,如图5和图6所示.可以看出,等效初始扭矩越大,形成稳定状态时它在环状杆上功也越大,扭矩沿弧长的分布就会越来越密集,幅值也越来越大;从图6所示的相图上看,稳定环的半径也越来越大.
由此可见,DNA的双螺旋结构在复制完成时,在酶的扭矩作用下,碱基链所代表的挠性线曲率振动幅值不断变大,封闭环所蕴含的能量也越来越大.图3所示相图中,圆环与横轴的左交点也逐渐靠近原点.由于(0,0)点为鞍点,所以挠性线曲率的最小值越接近0值,曲杆状态中出现直线状态越不稳定,当碱基链的曲率在受到外界干扰时极易跳跃到负值,即正反向扭转同时出现在一个DNA环中,杆的状态即出现失稳.
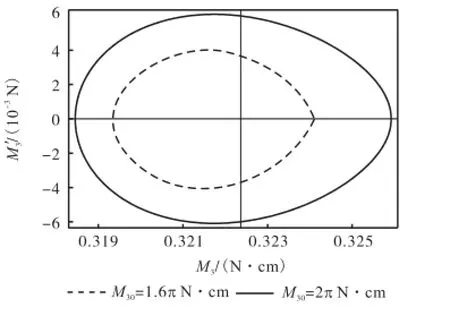
图5 扭矩周期变化的相图Fig.5 Thecurve

图6 扭矩随弧长变化的历程Fig.6 The s-M3curve
同样,根据式(23)和(25)所示的曲率变化情况,画出环状杆挠性线效果图,见图7和图8.
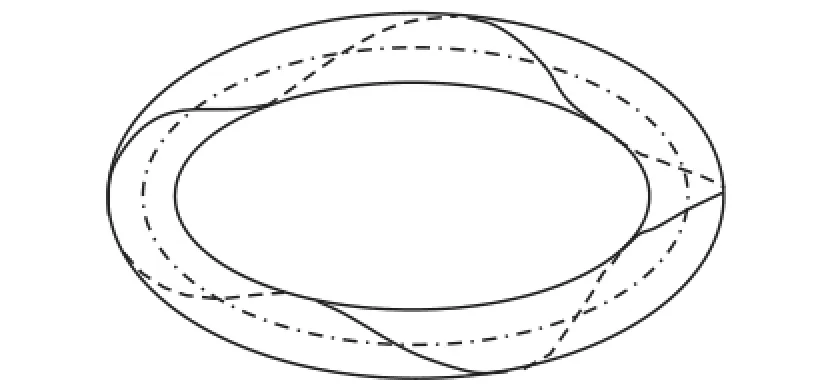
图7 M30=1.6π N·cm对应的挠性线效果图Fig.7 Flexibility of the rod with M30=1.6π N·cm
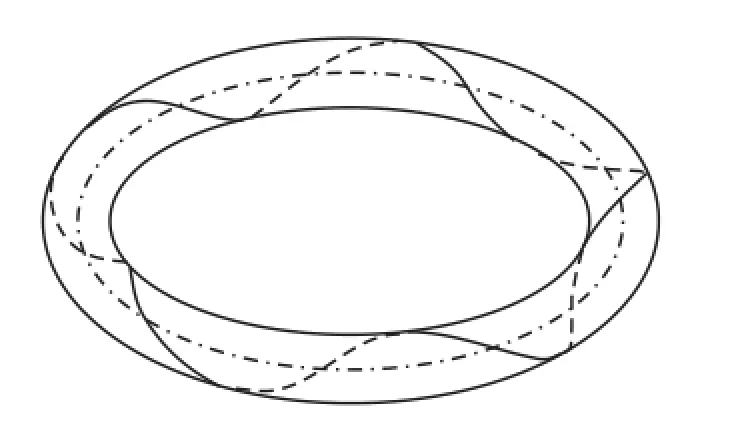
图8 M30=2π N·cm对应的挠性线效果图Fig.8 Flexibility of the rod with M30=2π N·cm
4 结 论
(1) 根据势能密度函数与哈密顿函数的形式相似性,引入等效初始扭矩的概念.结果表明,环状弹性杆作为一个封闭系统,其哈密顿函数的数值大小与等效初始扭矩的平方成正比关系,而初始自连接数与其一次方成正比关系,利用该参数,可以确定在DNA环复制、缠绕、螺旋和解螺旋等过程中,生物酶对封闭环的能量输入作用,以及对稳态构型形成机制的影响等功能.
(2) 运用非线性动力学思想对弹性杆扭矩模型进行了分析,系统分析了非对称截面Kirchhoff弹性杆扭矩沿模型所有平衡点的情况,并重点考虑和分析了符合实际情况的中心平衡点,以解析法为基础,分析了等效初始扭矩对该动力学模型的影响.在中心平衡点附近,当杆长以及杆的材料特性不变时,等效初始扭矩越大,环状弹性杆扭矩变化的圆频率越大,扭矩和挠性线曲率分布的变化范围和幅值也就越大,在相图中的运动轨线就越接近原点,正反绕向挠性线的同时存在,将导致DNA双碱基链在扭转过程中极易出现失稳情况.
(3) 本文分析过程及结论体现了解析方法的优势,即以直观的方式表现出参数变化对弹性杆构型的动态、连续影响.相图中平衡点稳定的中心特性也使得方程解析解的稳定性更具说服力,当然这也体现了李雅普诺夫理论无需求解即可判定解的稳定性的优点.相比数值方法来说,该解析表达式的形式更为直观简便,计算规模却要小很多.本文结果同样与Monta Carlo积分得出的结果相一致,符合能量最小原理的要求.本文分析过程不仅对于非对称截面弹性杆的研究适用,对其他以Kirchhoff方程为基本模型的弹性杆研究也同样具有重要的应用价值.
[1] Hoffman K A,Manning R S,Maddocks J H. Link,twist,energy,and the stability of DNA minicircles[J]. Biopolymers,2003,70(2):145-157.
[2] Furrer P B,Manning R S,Maddocks J H. DNA rings with multiple energy minima[J]. Biophysical Journal,2000,79(1):116-136.
[3] Stump D M,Watson P J,Fraser W B. Mathematical modelling of interwound DNA supercoils[J]. Journal ofBiomechanics,2000,33(4):407-413.
[4] Shi Yaoming,Hearst J E. The Kirchhoff elastic rod,the nonlinear Schrödinger equation,and DNA supercoiling[J]. Journal of Chemical Physics,1994,101(6): 5186-5200.
[5] 刘延柱. 弹性细杆的非线性力学——DNA力学模型的理论基础[M]. 北京:清华大学出版社,2006.
Liu Yanzhu. Nonlinear Mechanics——Thin Elastic Rod-Theoretical Basis of Mechanical Model of DNA[M]. Beijing:Tsinghua University Press,2006(in Chinese).
[6] Liu Yanzhu,Xue Yun. Stability analysis of helical rod based on exact Cosserat model[J]. Applied Mathematics Mechanics,2011,32(5):603-612.
[7] Liu Yanzhu,Sheng Liwei. Stability and vibration of a helical rod constrained by a cylinder [J]. Acta Mechanica Sinica,2007,23(2):215-219.
[8] 薛 纭,刘延柱. Kirchhoff弹性直杆在力螺旋作用下的稳定性[J]. 物理学报,2009,58(10):6437-6442.
Xue Yun,Liu Yanzhu. Stability of a straight Kirchhoff elastic rod under the force screws[J]. Acta Physica Sinica,2009,58(10):6437-6442(in Chinese).
[9] Xue Yun,Liu Yanzhu,Chen Liqun. Schrödinger’s equation for the Kirchhoff elastic rod with non-circular cross section [J]. Chinese Physics,2004,13(6):794-797.
[10] 王 炜,张琪昌,靳 刚. 非对称截面Kirchhoff弹性细杆模型简化方法研究[J]. 物理学报,2011,61(6):0646021-0646026.
Wang Wei,Zhang Qichang,Jin Gang. The analytical reduction of the Kirchhoff thin elastic rod model with asymmetric cross section[J]. Acta Physica Sinica,2011,61(6):0646021-0646026(in Chinese).
[11] Leung A Y T,Zhang Q C. Complex normal form for strongly non-linear vibration systems exemplified by Duffing-van der Pol equation[J]. Journal of Sound and Vibration,1998,213(5):907-914.
[12] Wang Wei,Zhang Qichang,Feng Jingjing. Global bifurcations of strongly nonlinear oscillator induced by parametric and external excitation[J]. Science China,2011,54(8):1986-1991.
Topological Configuration of Kirchhoff Thin Elastic Ring Rod with Asymmetric Cross Section
Zhang Qichang1,2,Zhao Bin1,2,Wang Wei1,2
(1. School of Mechanical Engineering,Tianjin University,Tianjin 300072,China;2. Tianjin Key Laboratory of Nonlinear Dynamics and Chaos Control,Tianjin University,Tianjin 300072,China)
Considering the forces and torques acted on the Kirchhoff thin elastic ring rod with asymmetric cross section,equivalent initial torque was introduced as a new concept to reveal the quantitative relationship between the state properties and parameters of torque dynamic model,which determines the configuration of the ring rod. As there exists formally a similarity between the potential energy density function and the Hamiltonian function,the quantitative relationship was obtained,which connects the equivalent initial torque,Hamiltonian function and initial link number. With DNA ring molecule as the physical background,this paper made the nonlinear dynamic analysis of torque model,and used undecided fundamental frequency method to obtain the asymptotic expressions for steady state periodic solutions around the practical equilibrium point. When the equivalent initial torque took different values,the graph of arc length-torque and phase portrait were drawn. The curvature could be expressed by the torque function with the equivalent bending stiffness considered,which provides a new methodological way to understand and describe the stable topological configuration of DNA ring under the influences of biological enzymes.
Kirchhoff;thin elastic rod;DNA ring molecule;undecided fundamental frequency method;nonlinear dynamic;equivalent initial torque
O322
A
0493-2137(2013)12-1089-06
DOI 10.11784/tdxb20131206
2012-05-11;
2012-09-02.
国家自然科学基金资助项目(11072168);高等学校博士学科点专项科研基金资助项目(新教师类)(20100032120006).
张琪昌(1959— ),男,教授.
张琪昌,qzhang@tju.edu.cn.
时间:2013-11-08.
http://www.cnki.net/kcms/detail/12.1127.N.20131108.1610.017.html.

