基于流场品质的风洞导流片空间布置参数优化

胡彭俊，谷正气, ，鲍欢欢，张清林

(1. 湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙，410082；2. 湖南工业大学 机械工程学院，湖南 株洲，412008)

风洞是一种专门设计的空气试验研究装置，它用动力装置在其实验段内造成可调节速度的气体流，以进行各种类型的空气动力学实验研究[1-2]。一个好的风洞应该至少具有3个基本特征：较好的流场品质、较高的运行效率以及较好的试验能力。所谓流场品质，主要是指风洞实验段内的气流参数在时间和空间上的均匀程度[3]。流场品质的优劣决定了实验数据的精确与否，它对于汽车气动外形设计好坏的评价起着关键的作用。在资金和时间有限的情况下，数值风洞无疑是进行前期开发设计和实验过程中检验改进的最好方式。本文作者利用CFD对所研究的尚未建设的风洞实验段流场进行模拟计算可以及早发现风洞可能存在的缺陷和不足，这对于汽车风洞建设前期方案的论证提供了更为广泛的信息，为建设具有一流流场品质的风洞提供了理论依据。随着高速公路的迅猛发展以及汽车研发技术的不断提高，现代轿车的车速可达 200 km/h以上。为了满足汽车风洞实验技术和现代轿车的开发需求，以及出于经济性考虑，汽车风洞的流场品质应达到以下标准[4-5]，如表1所示。

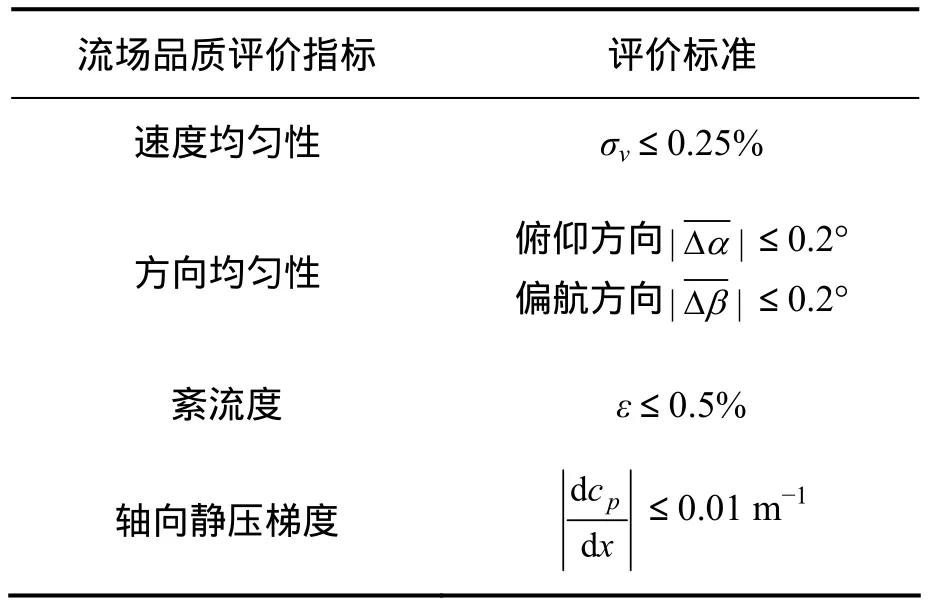
表1 汽车风洞流场品质评价指标Table 1 Evaluation index of automotive wind tunnel flow quality

1 计算模型和网格划分

导流片对实验段流场品质的影响采用如图1所示的模型进行计算研究，其稳定段内一般安装有蜂窝器和整流网以改善实验段内气流品质，蜂窝器的作用在于导直气流，使之平行于风洞轴线，消除气流的低频脉动以及和整流网一起消除空间的不均匀性，整流网的作用在于降低气流的紊流度。沿风洞拐角对称线布置一排垂直安放的导流片，称为拐角导流片，它的主要功能是降低拐角段阻力损失和提高拐角段出口流场的均匀性。在拐角导流片的工程应用中，需要确定导流片的空间布置参数，这些空间布置参数主要包括叶片弦长、数目(或间距)和安装角度[6]。

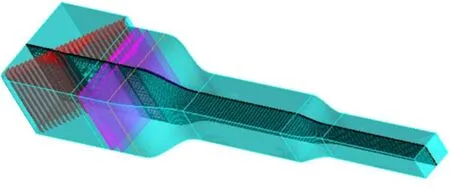
图1 风洞拐角段、稳定段、收缩段和实验段及其网格Fig. 1 Corner section, stable section, contraction section and test section of wind tunnel with related mesh

网格划分方式采用混合网格，为了减少网格数量、缩短计算时间和保证计算精度，在实验段和收缩段采用六面体网格，拐角段和稳定段采用四面体网格。拐角初始导流片的空间布置参数：弦长为1 917.1 mm，数目为24片，安装角为47°，整个计算模型的网格总数为430万，节点数为94万。

2 数值模拟

本文利用FLUENT软件平台，针对拐角流动进行数值模拟，该软件可针对各种复杂的流动现象，采用不同的离散格式和数值方法，并且包括了目前CFD中常用的各种湍流模型，在交通运输、航空航天等领域的流体力学数值模拟中得到了广泛应用。

2.1 边界条件的设定

设置计算域入口为速度入口边界，以风洞运行的最大速度进行考察，经计算，拐角入口处的速度应设为14.5 m/s。稳定段内的蜂窝器和整流网分别采用多孔介质和多孔跳跃来模拟，多孔介质参数根据压降与迎风风速的关系曲线确定得出，具体参数设置值如表2所示。

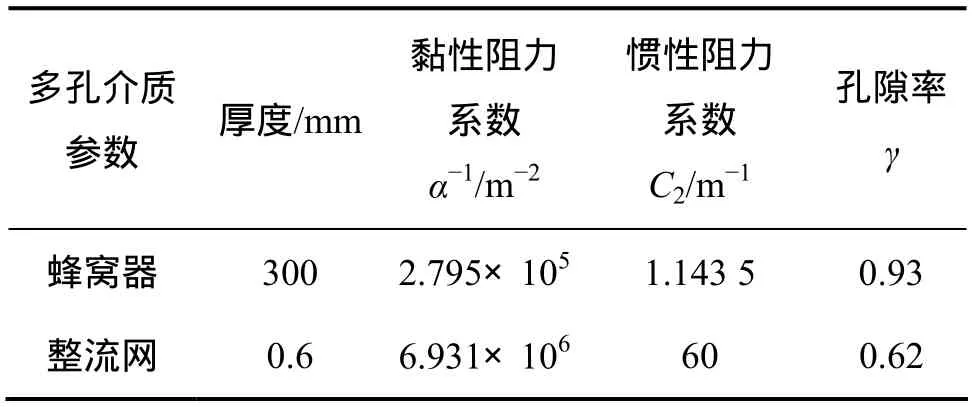
表2 蜂窝器和整流网的多孔介质参数Table 2 Porous media parameter of honeycomb and damping nets

2.2 数值模拟方法

FLUENT的湍流模型中，SST k-ω模型与标准k-ω模型相比，增加了横向耗散导数项，同时在湍流粘度定义中考虑了湍流剪切应力的输运过程，模型中使用的湍流常数也有所不同。这些特点使得SST k-ω模型的使用范围更广，比如可以用于带逆压梯度的流动计算、翼型计算、跨音速激波计算等等。曾敏等[7]比较了SIMPLE，SIMPLEC，SIMPLER和SIMPLEX 4种算法，得到 SIMPLEC具有较好的收敛性和健壮性。SIMPLEC算法与SIMPLE算法的思路基本一致，仅速度修正方法上有所改进，加快了收敛的速度。在拐角流动模拟中，导流片具有明显的逆压梯度，且包含导流片及洞壁在内具有较大面积的壁面条件，为了使计算加快收敛，选用SST k-ω湍流模型，采用SIMPLEC算法。

3 流场品质

研究拐角初始导流片对实验段流场品质的影响，需同时对实车实验段和缩比模型实验段进行分析。汽车实车实验段宽度为5.86 m，高度为4.5 m，长度为16 m，测试截面选取距实车实验段入口3，6和9 m的3个截面，分别标记为AA，BB和CC截面，如图2所示。每一个截面上共选择8种离地高度进行测试，与实车实验段地面的距离分别为0.5，1.0，1.5，2.0，2.5，3.0，3.5和4.0 m，每一高度分别取11个测试点，如图3所示。类似地，在宽为4 m，高为3 m，长为15 m的汽车缩比模型实验段，测试截面选取距模型实验段入口2.5，5.0和7.5 m的3个截面，分别标记为DD，EE和 FF截面，每一个截面的测试点共选择 5种离地高度进行测试，与风洞模型实验段地面的距离分别为0.5，1.0，1.5，2.0和2.5 m，每个高度分别取7个测试点，以下将基于这些测试截面上的测试点进行流场品质考察。

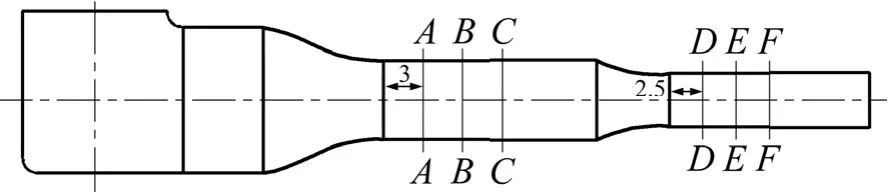
图2 汽车实验段测试截面Fig. 2 Test surfaces of automotive test section

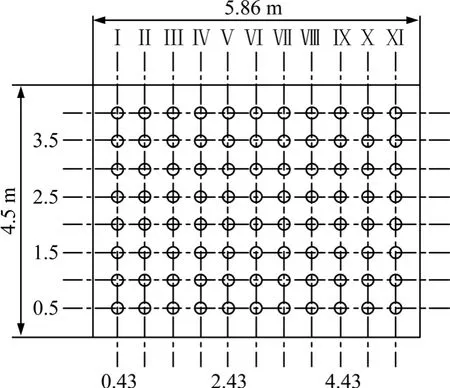
图3 汽车实车实验段各个截面上测试点的分布Fig. 3 Point’s distribution on test surface of full-scale automotive test section

3.1 速度的均匀性

速度的均匀性是指气流速度在空间的分布情况。要求实验段各点的速度完全一致是很困难的。一般要求风洞实验段模型区各个截面内各点的气流速度与气流平均速度相对偏差的均方根值小于某一给定值[8]。速度偏差的均方根为：

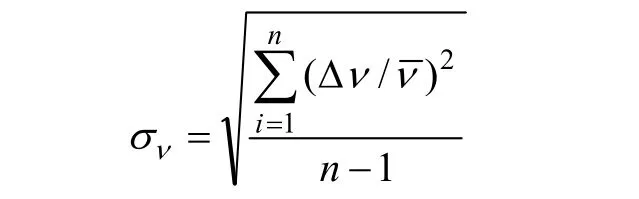
3.2 方向的均匀性

方向均匀性是指实验段模型区各个截面内任何一点的气流方向与风洞轴线之间的夹角[8]，主要包括俯仰角和偏航角，采用其平均值进行考察，AA，BB，CC，DD，EE和FF 截面平均俯仰角分别为0.110 05°，0.121 55°，0.134 02°，0.089 31°，0.120 56°和 0.120 94°，平均偏航角分别为 0.064 87°，0.048 14°，0.034 24°，0.031 75°，0.027 46°和0.026 54°，满足俯仰方向||αΔ≤0.2°和偏航方向||βΔ≤0.2°的要求。

3.3 紊流度

气流中存在着微小的旋涡运动，因而实验段任何一点的气流速度总存在着高频的微小脉动。某一点气流速度的瞬间值可以看作时均值和脉动值之和[8]。紊流度定义为3个方向脉动均方值的平均值，即：

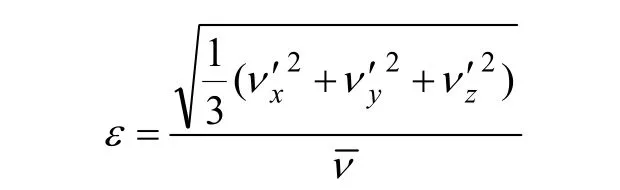
式中：ε为紊流度；xν′，yν′和zν′为速度在x，y和z方向的脉动值。其紊流度采用位于模型区的测试截面上的紊流度较大的点进行考察，AA，BB，CC，DD，EE和FF 截面紊流度的CFD计算值分别为0.562 7%，0.570 6%，0.503 0%，0.274 1%，0.357 2%和0.349 9%，基本满足ε≤0.5%的要求。

3.4 轴向静压梯度

对于闭口实验段，由于洞壁附面层顺气流方向发展，若不采取其他措施，会使有效流动截面缩小，主流速度增加，因而使压力沿气流方向不断降低，形成轴向静压梯度。于是，在流场中的物体受到一个沿轴向的附加压力，这在大气飞行中是不存在的。因而，风洞设计时应要求轴向静压梯度|dcp/dx|小于规定的值[8]。式中：p为当地压强；p∞为来流压强；v∞为来流速度；cp为压强系数。其中，cp定义为：

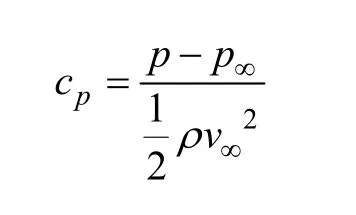
采用相邻截面中心点之间的静压梯度进行计算分析，AA与BB，BB与CC，DD与EE，EE与FF相邻截面中心点之间的静压梯度的 CFD计算值分别为0.540×10-3，4.220×10-3，1.049×10-3和 1.417×10-3m-1，完全满足|d cp/d x|≤0.01 m-1的要求。

4 导流片空间布置参数优化

4.1 优化问题描述

在初始导流片的基础上进一步分析了导流片其他空间布置参数时实验段的流场品质，对比发现速度均匀性和紊流度的变化比较明显，而方向均匀性和轴向静压梯度变动很小，同时在不同的点处紊流度会发生局部的突变，所以采用流场品质的速度均匀性评价指标来寻找较优的导流片空间布置参数组合。

优化导流片设计是拐角段降低气流损失的重要技术途径，本文将近似模型和优化算法等现代优化方法应用到导流片空间布置参数的设计当中。为减少工作量，假定弦长保持不变，对不同的导流片数目和安装角度组合进行优化，其优化流程如图4所示。

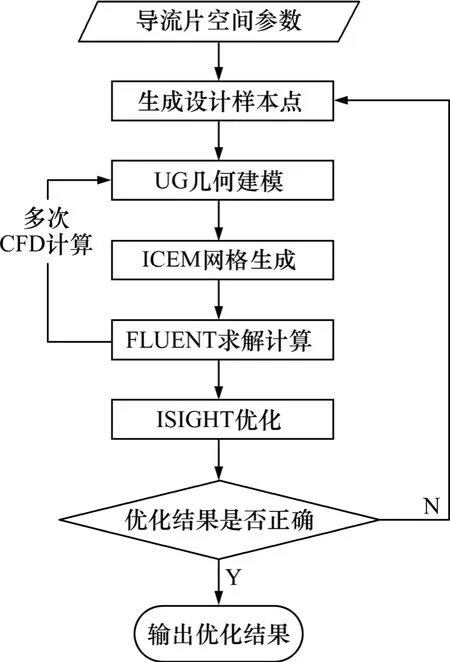
图4 优化流程图Fig. 4 Optimization flow chart

以导流片的数目和安装角为设计变量，其数目范围取为[21，28]，安装角范围取为[42°，48°]，且都为整数，以6个面的速度偏差的均方根σν的平均值为优化目标，在优化目标值达到最小时为最优，找出导流片空间布置参数的最优组合。

遗传算法是一种全局搜索优化算法，基本思想是基于达尔文“最适者生存”理论。它将问题表示成群体，根据适者生存的原则，从中选择出适应环境的个体进行复制，通过交叉、变异基本操作产生新一代更适合环境的群体，最后收敛到一个最优个体，求得问题的最优解[9]。

优化算法选择多岛遗传算法（MIGA)[10-11]，该算法是在传统遗传算法基础上发展起来的，继承了遗传算法的基本思想，两者的最大区别在于后者将众多种群分为若干个子种群（也成为岛)，在子种群中执行遗传算法的选择、交叉、变异等操作，并且周期性的在不同的岛之间有针对性的进行移民操作，能有效抑制优化的早熟现象。

4.2 试验设计和近似模型

试验设计是利用数理统计学和正交性原理，从大量的试验点中选取合适的且有代表性的点，应用正交表来合理安排试验的一种设计方法，本文根据拉丁超立方抽样方法[12]生成 14组样本点，将设计变量用于生成相应的UG模型并进行CFD模拟计算，得到14组响应值。

近似代理模型是指在不降低计算精度情况下构造的一个计算量小、计算周期短，但计算结果与数值分析或物理试验结果相近的数学模型，本文采用Kriging模型[13-15]，根据上述的 14组样本点及其响应值建立起设计变量与优化目标之间的近似模型。

4.3 优化过程和结果分析

设置种群数为20，岛屿数为10，迭代代数为50，计算得出模型最优解，此时最优设计目标值为0.078 45%，此时优化目标的CFD计算值为0.079 70%，相对误差仅为1.5%，可以认定此时设计目标值达到最优时所对应的空间布置参数组合是导流片数目为 27片，安装角为 47°。另外，为了验证此时各个截面速度偏差均方根的优化值和CFD计算值是否一致，又利用多岛遗传算法进行了相关计算，Isight和CFD计算所得出的测试截面的速度偏差的均方根 σν如表 3所示，每个截面的误差均控制在3%以内。

设计变量对优化目标的影响关系如图5所示，可见导流片安装角度a和数目b与速度偏差均方根的平均值y呈负相关，且导流片数目的负相关影响较大；图中a-b表示a与b的相互关系，可见a与b之间并不是相互孤立的，存在交互效应。

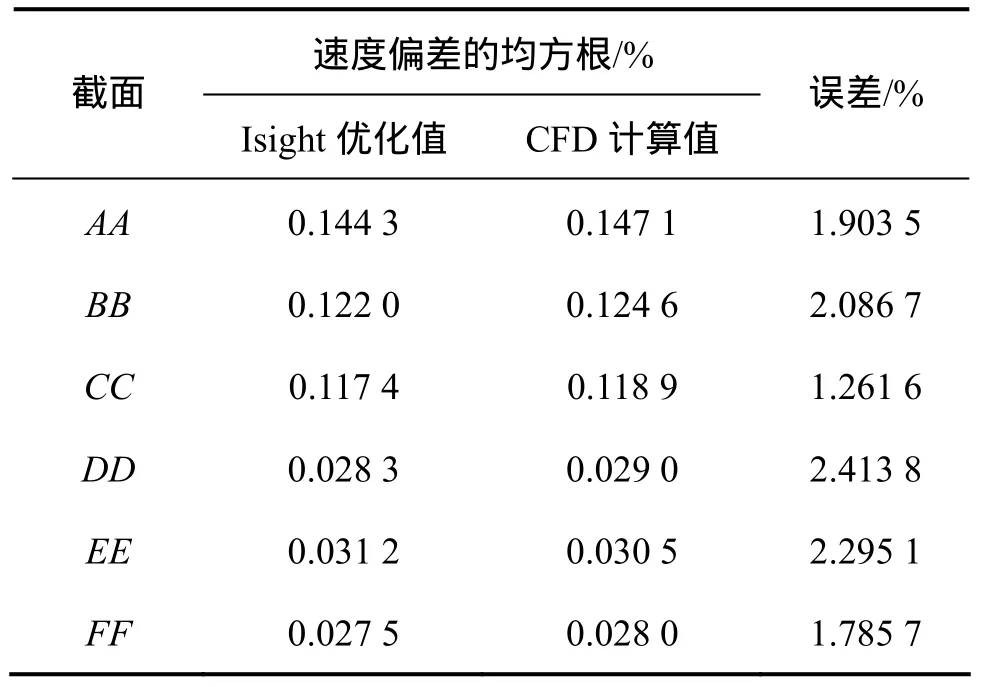
表3 Isight和CFD速度偏差的均方根计算值对比Table 3 Contrastion between Isight and CFD on root mean square of velocity deviation

4.4 流场品质对比

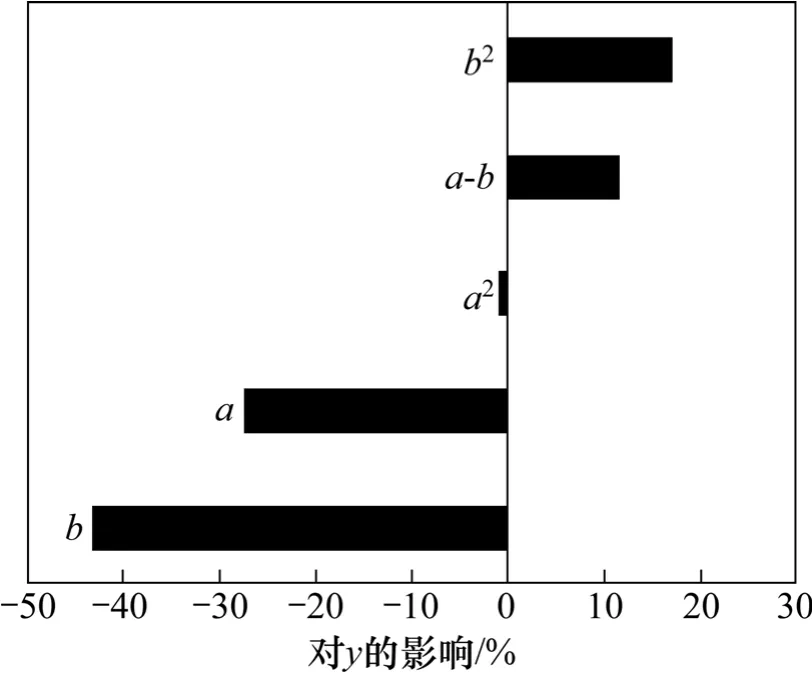
图5 设计变量对优化目标的影响Fig. 5 Influence of design variables on optimization objective

比较导流片在优化空间布置参数和初始空间布置参数2种情况下的流场品质，其数据如表4所示。由表4可见：优化空间布置参数相比初始空间布置参数的导流片，实车实验段和模型实验段的速度均匀性和紊流度明显降低，分别如图6～9所示；AA截面和BB截面平均俯仰角减少，在其他截面有所增加；AA截面和CC截面平均偏航角减少，在其他截面有所增加，但是幅度都较小。另外，优化空间布置参数时 AA与BB，BB与CC，DD与EE，EE与FF相邻截面中心点之间的静压梯度分别为0.515×10-3，4.210×10-3，1.049×10-3和1.417×10-3m-1，与初始布置比，基本没变化。可知在基于改进流场品质的情况下，导流片的优化空间布置参数比初始空间布置参数要优越得多，在一定程度上改进了风洞实验段的流场品质。

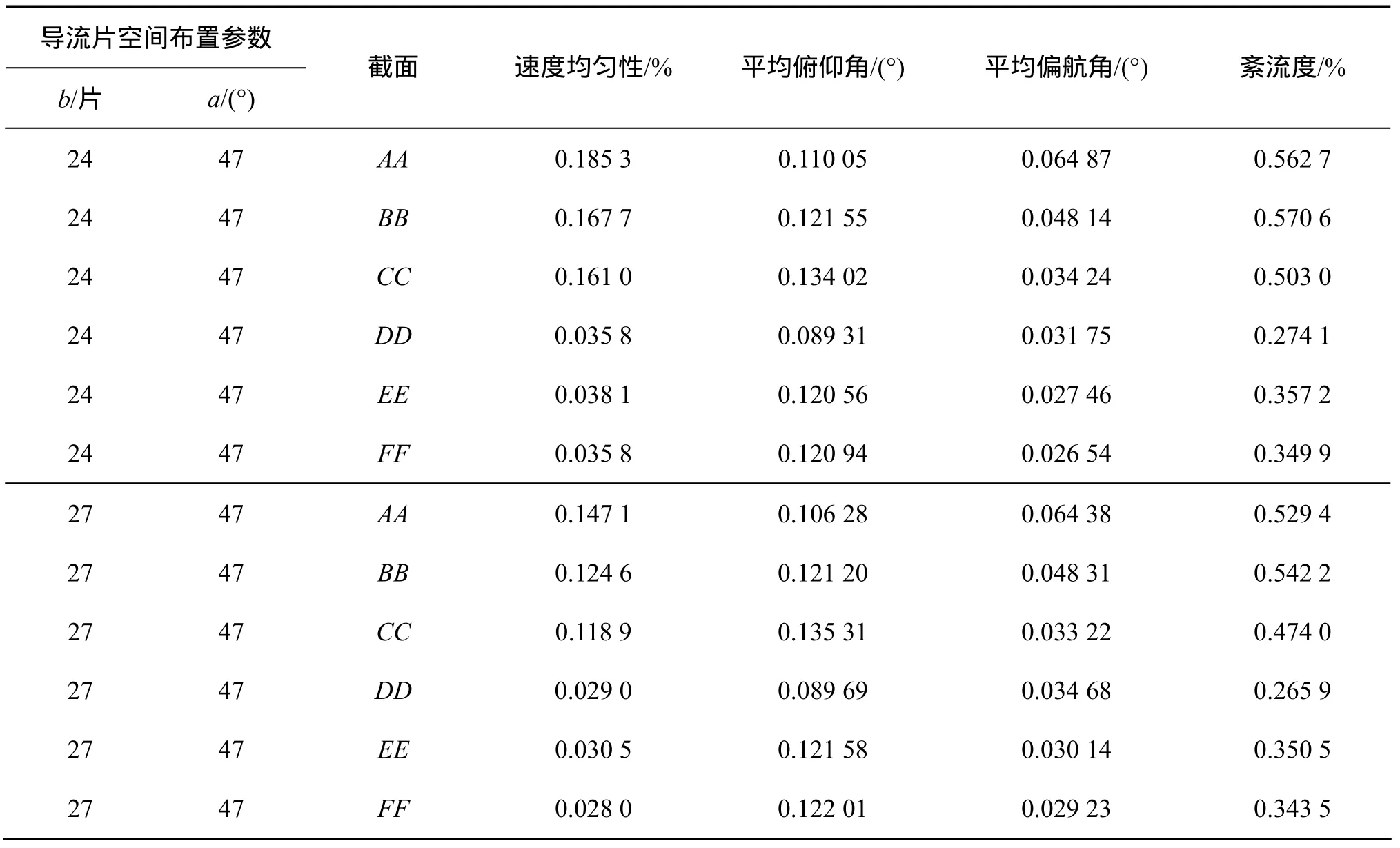
表4 导流片在两种空间布置参数情况下的流场品质对比Table 4 Contrastion of flow quality under two different layout parameters of deflector

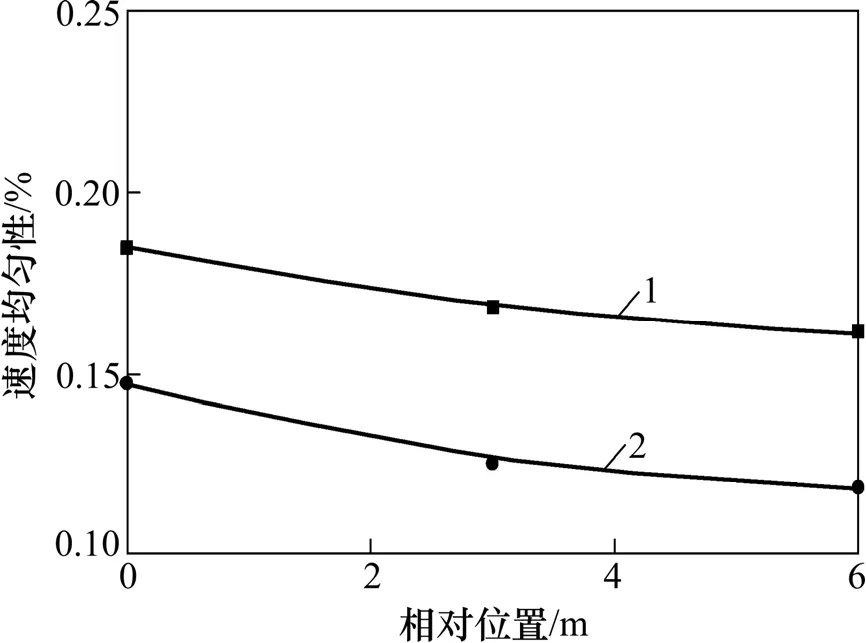
图6 实车实验段速度均匀性对比Fig. 6 Contrastion of speed uniformity in full-scale automotive test section

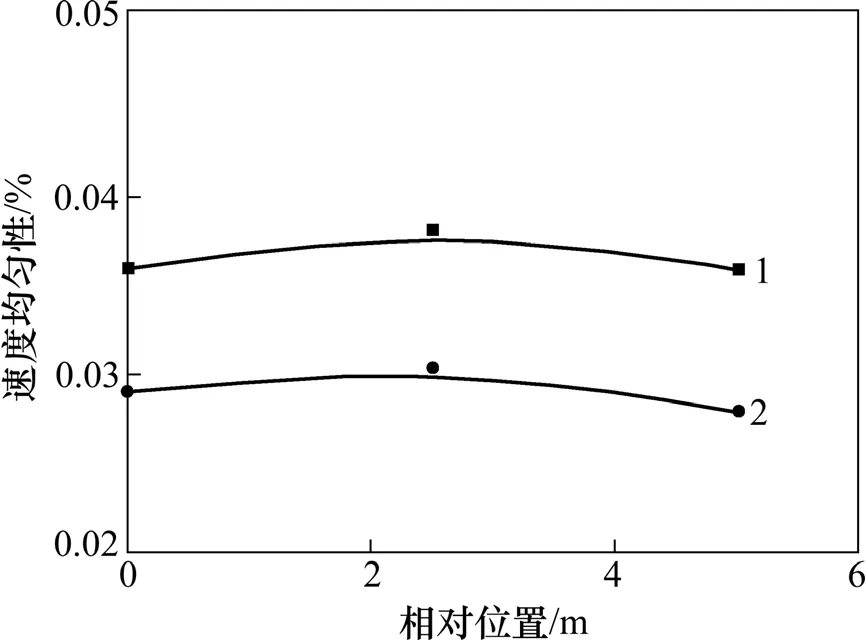
图7 模型实验段速度均匀性对比Fig. 7 Contrastion of speed uniformity in model automotive test section

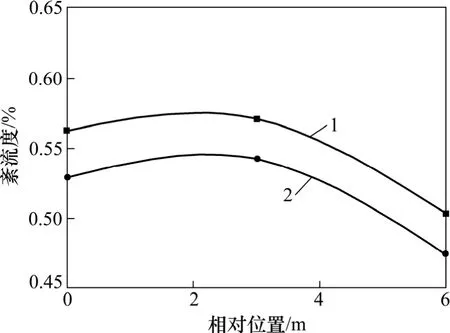
图8 实车实验段紊流度对比Fig. 8 Contrastion of turbulence intensity in full-scale automotive test section

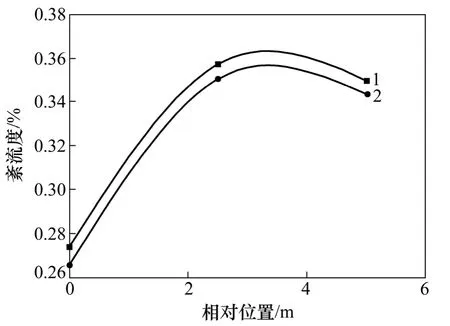
图9 模型实验段紊流度对比Fig. 9 Contrastion of turbulence intensity in model automotive test section

5 结论

(1) 利用CFD对风洞拐角初始导流片进行流场品质分析，并基于 Kriging模型建立风洞拐角导流片的近似模型，通过多岛遗传算法在保证弦长为 1 917.1 mm不变的情况下对实验段流场品质的速度均匀性指标进行优化，以导流片的数目和安装角为设计变量，速度偏差的均方根σν的平均值为优化目标，在优化目标值达到最小时为最优，得到导流片空间布置参数最佳组合是数目为27片，安装角为47°。

(2) 优化目标值为 0.078 45%，CFD计算值为0.079 70%，相对误差仅为1.5%，可见优化的可信度，为今后的虚拟风洞研究提供了一定的参考。

(3) 综合流场品质评价的指标，与初始导流片相比，在一定程度上提高了风洞实验段流场品质。

[1] 谷正气. 汽车空气动力学[M]. 北京: 人民交通出版社, 2005:212-220.GU Zhengqi. Automotive aerodynamics[M]. Beijing: China Communications Press, 2005: 212-220.

[2] 王文奎, 石柏军. 低速风洞洞体设计[J]. 机床与液压, 2008,36(5): 93-95.WANG Wenkui, SHI Baijun. The design of low speed wind tunnel[J]. Machine Tool & Hydraulic, 2008, 36(5): 93-95.

[3] 王勋年. 低速风洞试验[M]. 北京: 国防工业出版社, 2002:67-92.WANG Xunnian. Test of low speed wind tunnel[M]. Beijing:National Defense Industry Press, 2002: 67-92.

[4] GJB ll79—1991. 高速风洞和低速风洞流场品质规范[S].GJB ll79—1991. The standard of flow field quality for high speed wind tunnel and low speed wind tunnel[S].

[5] Carr G W, Cooper K R, Gilhaus A M, et al. Aerodynamic testing of road vehicles-testing methods and procedure[R]. Warendale PA: SAE Standards Committee, 1993: 14-16.

[6] 易星佑. 低阻损拐角导流片技术研究[D]. 绵阳: 中国空气动力研究与发展中心, 2009: 8-12.YI Xingyou. Research of corner vanes technique on low pressure loss[D]. Mianyang: China Aerodynamics Research and Development Center, 2009: 8-12.

[7] 曾敏, 陶文铨. 密网格下 SIMPLE等四种算法的收敛性与健壮性的比较[J]. 热科学与技术, 2003, 2(1): 90-93.ZENG Min, TAO Wenquan. Convergence characteristics of the SIMPLE series of algorithms in fine grid[J]. Journal of Thermal Science and Technology, 2003, 2(1): 90-93.

[8] 伍荣林, 王振羽. 风洞设计原理[M]. 北京: 北京航空学院出版社, 1985: 22-26.WU Ronglin, WANG Zhenyu. Design principles of wind tunnel[M]. Beijing: Beihang University Press, 1985: 22-26.

[9] 容江磊, 谷正气, 杨易. 基于 Kriging模型的跑车尾翼断面形状的气动优化[J]. 中国机械工程, 2011(2): 243-246.RONG Jianglei, GU Zhengqi, YANG Yi. Aerodynamic optimization of cross sectional shape for a sports car's rear wing based on Kriging Surrogate model[J]. China Mechanical Engineering, 2011(2): 243-246.

[10] 赵志国, 司传胜. 基于多岛遗传算法的铰接车轮边减速器优化设计[J]. 机械设计与制造, 2010(12): 213-215.ZHAO Zhiguo, SI Chuansheng. Application of miga to design of optimization for wheel hub reducer in articulated dump truck[J].Machinery Design & Manufacture, 2010(12): 213-215.

[11] 宋昕, 谷正气, 张清林. 基于多岛遗传算法的湍流模型优化研究[J]. 湖南大学学报, 2011, 38(2): 23-29.SONG Xin, GU Zhengqi, ZHANG Qinglin. Study of the turbulence model optimization based on multi-island genetic algorithm[J]. Journal of Hunan University, 2011, 38(2): 23-29.

[12] 陈魁. 试验设计与分析[M]. 北京: 清华大学出版社, 2005:97-100.CHEN Kui. Design and analysis of experiments[M]. Beijing:Tsinghua University Press, 2005: 97-100.

[13] 游海龙, 贾新章. 基于遗传算法的Kriging模型构造与优化[J].计算机助设计与图形学学报, 2007, 19(1): 64-68.YOU Hailong, JIA Xinzhang. The construction and optimization of Kriging metamodel based on Genetic Algorithms[J]. Journal of Computer-aided Design & Computer Graphics, 2007, 19(1):64-68.

[14] Jones D R, Schonlau M, Welch W J. Efficient global optimization of expensive black-box functions[J]. Journal of Global Optimization, 1998, 13: 445-492.

[15] Lophaven S N, Nielsen B, Sondergaard J. DACE-A Matlab Kriging Toolbox[R]. Copenhagen: Technical University of Denmark, 2002: 2-9.