面向有效载荷质量的平流层飞艇设计参数优化

张礼学，王中伟，杨希祥

(国防科技大学 航天与材料工程学院，湖南 长沙，410073)

临近空间是介于航空和航天领域之间的一段空域，目前人类飞行活动还很少涉及。近年来，随着临近空间飞行器在区域大气环境监测、防震减灾、高分辨率对地观测、区域紧急通信救援等任务中的优势被发现，世界各国纷纷投入大量的人力物力进行平流层飞艇的研制。在飞艇设计中的各个阶段，特别是概念设计阶段，性能指标的选择与优化十分重要。它不但决定着设计方案的经济性，许多时候还对飞艇设计方案的可行性产生深远影响。国内外关于飞艇性能指标的选择与优化的研究很早就已经开展，但相当一部分是针对低空飞艇进行的，只有很少一部分尝试对平流层飞艇进行展开。其中，Mueller等[1-2]在总结前人工作基础上发展了高空飞艇的六自由度飞行数值分析模型，并在考虑平流层飞艇太阳能获取模型的基础上进行了飞艇的航迹优化。Colozza[3]对平流层飞艇设计方案的可行性预估模型进行了初步研究，但研究中只考虑了能源平衡约束。Pant[4]对非硬式飞艇从几何外形、阻力、推力等3个子系统进行了经验建模，并基于这些模型提出了一种初步设计飞艇的方法，并进行了设计参数的灵敏度分析。姚伟等[5-10]对平流层飞艇的设计参数灵敏度进行了分析，Wang等[10]基于MDO方法对飞艇外形进行了优化。王海峰等[7]研究了高空飞艇的总体设计方法并基于有限元思想进行了薄膜太阳能电池曲率对飞艇太阳能获取能力的影响分析。在上述文献的相关研究中，阻力最小、质量最轻、拉应力最小等成为最常用的优化目标，而平流层飞艇的飞行任务一般是携带高分辨率雷达(通信设备)实施高空对地观测任务(通信)或者是利用其经济的运输成本进行远程的大规模的物资输送，因此飞艇能提供的有效载荷质量能力才应该成为衡量该设计方案优劣的重要指标。此外，文献研究中对平流层飞艇设计过程中的约束条件考虑不全也是需要重点改进的地方。为此，本文作者提出了以平流层飞艇最大有效载荷质量为优化目标，综合考虑能源平衡、材料强度等方面约束的平流层飞艇设计参数优化模型。希望通过相关研究为平流层飞艇的设计提供一定的理论和技术支持。

1 平流层飞艇性能指标估算模型

1.1 飞艇外形几何参数

平流层飞艇的几何外形可近似的用2个半椭球旋成代替，其二维平面图如图1所示，其囊内体积可通过下式进行计算：

式中：V为飞艇体积；a1，a2分别为2个椭球的长半轴长；b为2个椭球的短半轴长；l和d分别为飞艇的艇长和最大直径。其表面积可由式(2)计算：

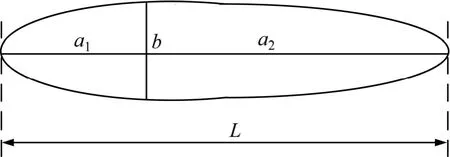
图1 飞艇外形参数示意图Fig. 1 of airship’s shape parameter

并可定义飞艇的长细比为：

1.2 大气阻力估算

平流层飞艇的阻力大部分由艇身产生，在进行飞艇早期设计时可认为飞艇阻力等于飞艇裸艇体阻力。飞艇的艇体阻力系数可用下式进行估算：

式中：Cd为飞艇阻力系数；Re为飞艇雷诺数。其中雷诺数的计算公式为：

其中：ρ∞为周围环境大气密度；U为飞艇飞行速度；μ∞为黏性系数，其计算公式如下：

其中：T∞=T为周围环境温度，s=C为常量110.4 K，μ0是 15 ℃(即 T0=288.15 K)时空气的 μ 为 1.789×10-5Pa·s。平流层飞艇在飞行过程中所承受的大气阻力可表示为：

式中：Fd为飞艇所受阻力。进而可估算出平流层飞艇推进系统每天所需耗费能量为：

其中：ηp为推进系统的总效率，一般推进系统的效率在0.7到0.9之间，这里取为0.9。

1.3 平流层飞艇太阳能获取能力估算

能够长时间驻空飞行是平流层飞艇不同于低空飞艇和高空探测气球的主要特点。在平流层飞艇上，如果采用自身携带燃料电池等来提供所需能源，其携带的电池质量将随时间呈正比增加。当时间长度超过一定限度时，飞艇将为此付出沉重的代价。而基于薄膜太阳能电池和锂离子蓄电池或再生式燃料电池等组成的闭环式再生能源系统，其质量不会随着时间的延续而增加。因此，采用背铺柔性薄膜太阳能电池吸收太阳能提供能量来源，利用锂离子电池和再生燃料电池储藏剩余能量以备飞艇黑夜和紧急情况的需要的设计方案成为目前平流层飞艇设计方案中广泛采用的形式。

在平流层飞行的飞艇能够获取的太阳能受很多因素影响，这些因素大体可以分为2类：自然因素类(如飞行时间，驻留地理位置等)和飞艇设计因素类(如飞艇长度、太阳能电池铺设面积、曲率半径、飞行姿态等)。由于太阳能电池一般铺设在其背部平坦的中段，进行能源估算时可以将这一段区域近似为圆柱体。在圆柱体的表面上，任一小单元的坐标可以表示为[10]：

式中：γ为太阳能电池铺设圆周半径角。则该小单元的单位方向向量可表示为：

当平流层飞艇驻空飞行时，由于平流层中大气的风向一般自东向西，飞艇一般迎风飞行，所以假设飞艇艇首方向向东，并设其俯仰、偏航和侧滑角均为零，则太阳的方向向量可以表示为：

其中：α为太阳时角，其24 h内变化约为360°，上午太阳时角为负值，下午太阳时角为正，可用下式计算：式中：t为太阳时，以24 h计。β为太阳高度角，可由下式计算得到：

这时，方向角为n的单块太阳能电池上太阳辐射强度为：

整个飞艇艇身上的太阳能电池阵列在1 d中所能产生的总能量为

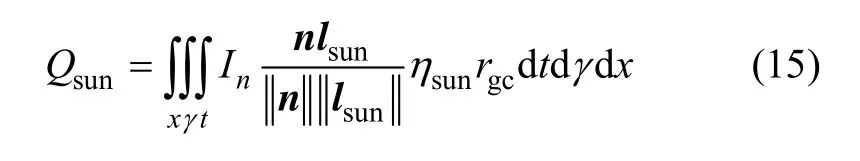
在飞艇能源平衡的前提下(即 Qsun≥Wp)，所需太阳能电池铺设面积为

令太阳能电池阵列的密度为ρdc，则平流层飞艇由于背铺太阳能电池而增加的质量为

1.4 飞艇蒙皮张应力系数估算

平流层飞艇的设计由于对质量等条件有苛刻的限制，一般采用软式或半硬式结构，与硬式飞艇不同，平流层飞艇的蒙皮还要起到保形的作用，它通过飞艇艇囊的内外压差 ΔP来实现。但飞艇内外压差的存在也使得蒙皮要承受一定张力，而且由于飞艇不同位置的曲率半径不一样致使蒙皮上各处的张力也不同。文献[9]在进行曲率半径不等时蒙皮所受应力分析时指出，随着曲率半径比的增大,一个方向的张力系数趋近于 0，另一个方向上的张力系数趋近于一个定值。因为飞艇的轴向曲率半径非常大，在进行张力系数估算时，可以将其看成是承受内压的薄壁圆筒进行分析，则作用于艇囊横截面单位长度上的最大张力系数σ可用式(18)表示：

式中：d为艇囊横截面内径。同时可知，随着飞艇内外压差和囊体内径的增加，艇囊蒙皮所承受的应力就会成正比例上升。当选用的囊体材料确定后，蒙皮的极限强度σ0也就确定了，艇囊内外压差和内径的选择应该满足 σ≤σ0。

1.5 平流层飞艇携带有效载荷质量能力估算

当平流层飞艇为常见的保形设计时，飞艇在整个飞行过程中体积保持不变。当不考虑氦气泄漏影响，并假设飞行过程中，飞艇内外压差保持不变以及飞艇的吸放气过程内外温度保持一致后，放飞时(海平面)，飞艇的净浮力计算公式为：

式中：Fb0为放飞时飞艇的净浮力；ρaw0为海平面大气密度；V为飞艇艇囊总体积(V=Va+Vhe)；Va为艇身内空气囊的总体积；ρan0为艇身空气囊内空气密度，相对应的 ρhe0，Vhe0分别为氦气囊内氦气密度和氦气囊总体积。假设囊体内外的压差恒定，为 ΔP(ΔP≥0)，当内外温度一致时，应用理想气体状态方程

则

综合式(19)，(20)和(21)后得：

在海拔高度为H的地方，飞艇所受净浮力为：

当囊体内外的压差恒定 ΔP(ΔP≥0)，内外温度一致时，类似的应用理想气体状态方程可得飞艇在高度为H的地方所受的净浮力为：

又因为飞艇在其上升过程中，氦气的质量保持不变，由理想气体状态方程，对于氦气，nR= 为常值。有

设 ΔP=k1×P0，Vhe0=k2×V，(0＜k1＜1，0＜k2＜1)，则有

为满足飞艇的纵向静平衡，飞艇的净浮力、自身质量ms和载荷质量mz应满足如下平衡关系：

其中自身质量又可以分为蒙皮质量 mmp、太阳能电池质量 mdc，即 ms=mmp+mdc。又 mmp=ρmpS，ρmp为蒙皮的密度，S为艇身的表面积，则平流层飞艇的有效载荷质量可表示为：

图2所示为长细比为3，背铺太阳能电池半径角度为π/2，长度为艇长1/3，最大张应力系数为75 440 N/m，内外压差为2 000 Pa情况下，飞艇艇长对飞艇有效载荷质量能力的影响。由图2可以发现：平流层飞艇的有效载荷质量能力随着艇长的增加先减小后增大。而且当长度小于120 m时，其载重能力为负；此后随着艇长的增大而迅速增加。当以最小质量为优化目标时，120 m是上述条件下飞艇的艇长，显然这不能反映飞艇的实际任务需求。

图3所示为基本条件和图2相同情况下，不同的飞艇长细比随飞艇长度变化对飞艇有效载荷质量能力的影响。由图3可以发现：在相同的艇长长度下，飞艇的有效载荷能力随着长细比的减少而增加。而当以阻力最小为优化目标时，上述条件下飞艇的最优长细比为4，而这显然也不能反映飞艇的实际任务需求。

图2 飞艇艇长对有效载荷质量的影响Fig. 2 Influence of airship length to payload mass

图3 飞艇长细比对有效载荷质量的影响Fig. 3 Influence of airship slenderness ratio to payload mass

图4所示为基本假设条件和图2相同情况下，飞艇艇囊内外压差变化对飞艇有效载荷质量能力的影响。由图4可以发现：飞艇的有效载荷质量能力随着内外压差的增加而减少。由此可见：飞艇的有效载荷质量能力除了跟飞艇几何外形参数相关外，也与其放飞初始参数紧密相关。

由以上分析可以发现：以阻力最小、质量最轻为目标进行的设计不能反映飞艇适应实际任务的需求。飞艇有效载荷质量能力与许多影响因素均有关系，在进行设计参数优化时应综合考虑阻力、浮力、能源、材料等多方面约束进行，每个因素都可能对飞艇的任务能力产生重要影响。

图4 飞艇内压对有效载荷质量的影响Fig. 4 Influence of airship ΔP to payload mass

2 优化模型

2.1 优化目标、变量及约束条件

平流层飞艇的飞行任务一般是携带高分辨率雷达(通信设备)实施高空对地观测任务(通信)或者是利用其经济的运输成本进行远程的物资输送。因此飞艇能提供的有效载荷质量应该成为衡量某设计方案优劣的重要指标。综合上述平流层飞艇各子系统的性能参数估算模型，可以确定平流层飞艇设计参数优化模型的优化目标函数为：

其中飞艇在地面充入氦气的体积比k2由飞艇的压力高度所决定，为了便于比较，本文以压力高度为21 km的平流层飞艇进行设计，其k2=0.06。式中的大气参数和材料参数可通过查表获取。优化变量取为飞艇艇长l、飞艇长细比f、内外压差系数k1、太阳能电池铺设半径角γ和太阳能电池铺设长度x。飞艇设计时，除了考虑推阻平衡、浮重平衡和能源平衡3种基本平衡约束外，还应考虑：

(1) 飞艇结构有足够的工作强度。

(2) 飞艇制造过程中制造工艺的约束，如飞艇艇长约束。

(3) 飞艇飞行过程的安全性能约束，如飞艇内外压差的约束。

综合上述约束条件，以最大有效载荷质量为优化目标的飞艇设计参数优化模型如下：

2.2 混沌粒子群优化算法

优化方法采用混沌优化和粒子群优化两者结合的混沌粒子群算法。该算法对于给定的优化函数，通过将搜索过程对应为混沌轨道的遍历过程，可使搜索过程具有避免陷入局部极小的能力。混沌搜索算法通常需要大量的迭代步数才能获得较好的解，且对初始解十分敏感，当其与粒子群算法结合时则可避免这一缺点。粒子群算法主要用于全局搜索，而混沌搜索则根据粒子群的结果进行局部搜索。因混沌粒子群算法只能求解一定约束形式的极小值问题，故本文首先将目标函数变为：

约束条件通过引入外点罚函数

将约束优化问题转变为适用于混沌粒子群优化算法的无约束优化问题。式中gj(x)为优化模型中的约束条件，M为与最小值相比量级较大的权重常量。

3 应用实例

本文以美国导弹防御局提出的平流层飞艇设计方案(HAA)为应用背景，其设计压力高度为 20 km，该处大气压力为5 520 Pa，密度为0.091 kg/m3，温度为216.7 K。设计飞行日期为12月25日，纬度为北纬40°，该处的太阳辐射强度为1 260 W/m2。此外由于现有制造工艺等条件的限制，σ0=75 440，lmax=200，fmax=20，0.02≤k1≤0.06，γmax=π/2。

为验证本文所提优化模型的有效性，基于目前常用设计经验设计了平流层飞艇参考设计方案。在2个设计方案中，蒙皮的面密度取为200 g/m2，蒙皮的最大抗拉应力系数为75 440 N/m。薄膜太阳能电池面密度为200 g/m2，其与蒙皮的复合方式为表面挂装。飞艇需要提供给任务载荷的功率设为恒定值(5 kW)，两方案的设计参数及最大有效载荷质量见表1。

从表1中参考和优化方案设计参数的对比可以看出，艇长、内外压差以及太阳能光伏电池的铺设长度的变化不大，而飞艇的长细比、半径角的变化较大，其中长细比减小11.9%，半径角减少50%。而综合优化后，同样长度飞艇的最大有效载荷质量增加了50%。这与飞艇长细比为4左右时，阻力系数最小的结论并不矛盾，主要是因为当飞艇的长细比在2.5到6之间变化时，飞艇的阻力系数变化不大，而飞艇体积却因此得到增加，体积的增加很大程度上提升了飞艇的净浮力。可见，平流层飞艇的设计是一个各子系统紧密耦合、相互制约的求解过程。某些单项性能指标的牺牲是为了系统任务指标的最优化。此外，考虑飞艇背铺柔性薄膜太阳能电池的曲率进行的太阳辐射功率估算比仅考虑太阳辐射在水平投影面内辐射功率的估算大很多[10]，因此优化后的太阳能电池所需面积下降了约一半。

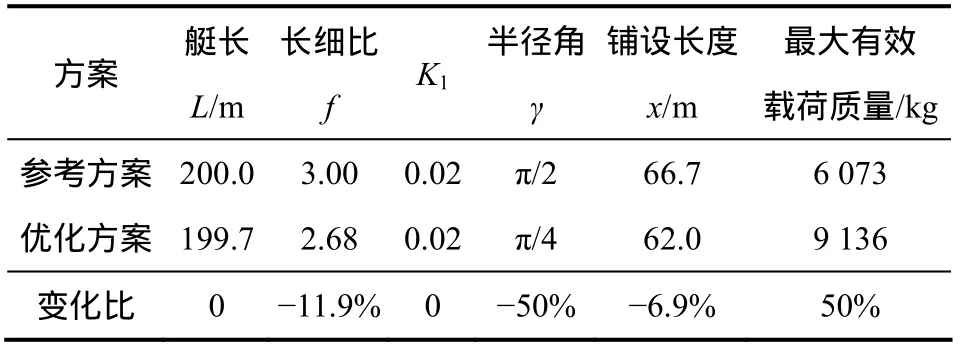
表1 设计方案的设计参数及最大有效载荷质量Table 1 Design parameters and maximum payload mass

4 结论

(1) 设计平流层飞艇时仅以阻力最小、质量最轻等为设计目标不能真实反映飞艇对其任务的适应能力，设定优化目标时必须结合事物本身的实际任务需求进行。

(2) 通过优化设计方案和经验参考方案的对比发现，平流层飞艇设计是一个各子系统紧密耦合、相互制约的求解过程，现有的许多飞艇设计经验值是在仅考虑单个子系统性能最优前提下得出的，将其应用于总体方案设计时，需要进行综合考查。

(3) 精确的估算模型对设计影响较大，考虑飞艇外形曲率进行的太阳能电池铺设设计比未考虑曲率的设计面积减少近一半。

[1] Mueller J B, ZHAO Yiyuan, Garrard W L. Development of aerodynamic model and control law design for a high altitude airship[C]//3rd “Unmanned Unlimited” Technical Conference.Chicago: AIAA. 2004: 1-17.

[2] MUELLER J B, ZHAO Yiyuan, GARRARD W L. Sensitivity and solar power analysis of optimal trajectories for autonomous airships[C]//Guidance, Navigation, and Control Conference.Chicago: AIAA, 2009: 1-18.

[3] Colozza A. Initial feasibility assessment of a high altitude long endurance airship[J]. Ohio: Analex Corporation, 2003: 35-40.

[4] Rajkumar S, Pant A. Methodology for determination of baseline specifications of a non-rigid airship[J]. AIAA 2003-6830.

[5] 姚伟, 李勇, 王文隽, 等. 平流层飞艇优化方法和设计参数敏感性分析[J]. 宇航学报, 2007, 28(6): 1524-1528.YAO Wei, LI Yong, WANG Wenjun, et al. Stratospheric airship optimization method and design parameters sensitivity analysis[J]. Journal of Astronautics, 2007, 28(6): 1524-1528.

[6] 安伟刚, 李为吉, 王海峰. 某型飞艇外形多目标优化设计及其决策[J]. 西北工业大学学报, 2007, 25(6): 789-793.AN Weigang, LI Weiji, WANG Haifeng. Multi-objective optimization design of envelope shape of a certain airship with deviations considered[J]. Journal of Northwestern Polytechnical University, 2007, 25(6): 789-793.

[7] 王海峰, 宋笔锋, 刘斌, 等. 高空飞艇总体设计方法研究[J].西北工业大学学报, 2007, 25(1): 56-60.WANG Haifen, SONG Bifen, LIU Bin, et al. Exploring configuration design of high altitude airship[J]. Journal of Northwestern Polytechnical University, 2007, 25(1): 56-60.

[8] 王文隽, 李勇, 姚伟, 等. 飞艇气囊压力与蒙皮张力的估算[J].宇航学报, 2007, 28(5): 1109-1112.WANG Wenjun, LI Yong, YAO Wei, et al. Estimation of the relationship between the pressure in airship[J]. Journal of Astronautics, 2007, 28(5): 1109-1112.

[9] 王海峰, 宋笔锋, 苏建民, 等. 高空飞艇薄膜太阳电池内辐射量计算研究[J]. 太阳能学报, 2006, 27(8): 819-823.WANG Haifeng, SONG Bifeng, SU Jianmin, et al. Computation research on the solar radiation on the thin film solar cell for high altitude airships[J]. Acta Energiae Solaris Sinica, 2006,27(8): 819-823.

[10] WANG Quanbao, CHEN Jian, FU Gongyi, et al. An approach for shape optimization of stratosphere airships based on multidisciplinary design optimization[J]. Journal of Zhejiang University, 2009, 10(11): 1609-1616.