宏程序在加工圆弧面中的应用
蒋晓敏
(江阴职业技术学院,江苏江阴 214405)
在数控加工中,经常会遇到各种各样的圆弧曲面的加工。最常见的就是XY面的圆弧,这种圆弧面可以通过G02/G03 圆弧指令的编程来完成加工,非常方便。
其他平面的圆弧面的加工,虽然使用G02/G03 圆弧指令来编程也能进行加工,但往往加工程序比XY面的圆弧要复杂,这时正确的做法是利用宏程序来编程。下面是应用宏程序精加工圆弧面的两个例子,当然在精加工前要进行粗加工,先铣削长方形轮廓,此处省略。
1 实例一:平行坐标平面的圆弧面的加工
1.1 实例说明
如图1 所示,该圆弧面在G18 平面(XZ 平面)内的投影为圆弧。该圆弧半径为30 mm,投影到XY面为长48 mm,宽25 mm的长方形,长方形的2 个边分别平行于X、Y 轴,长方形关于Y 轴对称。
1.2 确定编程思路
加工该圆弧常见的有两种方法。一种方法就是用G02/G03 指令编制G18 平面的圆弧指令,可以实现圆弧面的加工。看到的是一条圆弧,在加工中,必须把左半个圆弧与右半个圆弧分开,用2 个圆弧指令,中间还要加上直线段指令来过渡(因为刀具直径的缘故)。然后沿着Y 方向移动一个较小的间隔,再用G02/G03 指令铣削一步加工,依次循环,直到圆弧面的长度尺寸满足图纸的要求为止。

图1 平行坐标平面的圆弧面立体图
另一种加工方法采用拟合的方法,刀具在某一个X位置,沿Y方向走直线;然后沿Z方向抬一个很小的距离,刀具移动至另一个X位置,再沿Y方向走直线,这样依次循环,实现圆弧的加工。
这里选第二种方法,用宏程序来完成该圆弧面的加工。
虽然球头铣刀在加工圆弧面时的工件表面质量好,但是键槽铣刀编程较球头铣刀容易,数值计算也更容易,且移动的步距适当小的时候,一般也能够满足工件的表面质量要求。故这里选用12 mm键槽铣刀,机床为FANUC数控系统,取前侧圆弧的最高点为工件原点,见图2。
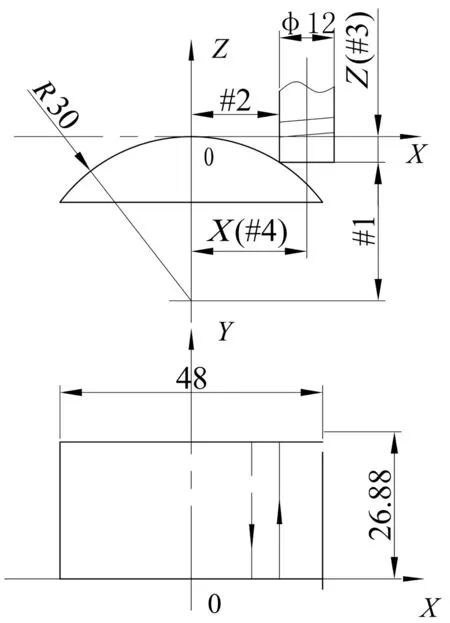
图2 数学模型
1.3 数学模型[1]
#1:刀具底面到圆弧中心的距离;
#2:刀刃到圆弧对称中心的距离;
那个用木头搭建的,小得像工地上临时住所一样的家,被台风撕成了一堆破木头,温衡站在这堆木头前,没有哭,她已经习惯了这种突如其来的灾祸。她蹲下来,在一堆木头里,寻找还没有被损坏的东西和她的存钱罐,就像在她命途多舛的生命里,寻找渺小的希望。
#3:Z坐标值;
#4:X坐标值。
1.4 加工程序


2 实例二:非平行坐标平面的圆弧面的加工
非平行坐标平面的圆弧面立体图如图3所示。

图3 非平行坐标平面的圆弧面立体图
2.1 与实例一的对比
该圆弧面的尺寸与图1 完全一样,变化前的数学模型如图4 旋转前的数学模型;变化在于圆弧在XY面旋转了一定角度,其数学模型如图5旋转后的数学模型。
2.2 确定编程思路
用G02/G03 指令编程不能实现加工这样的圆弧面,因为该圆弧面不平行于任一个坐标平面。换个思路,可以把它看作在XY 面旋转了一个角度。因此,在编程时就可以结合G68/G69坐标旋转功能来实现加工的要求,只要在例一的程序中加入这2 个指令就可以了。考虑到程序的通用性,把圆弧面的各个尺寸和刀具的直径都用变量来表示。
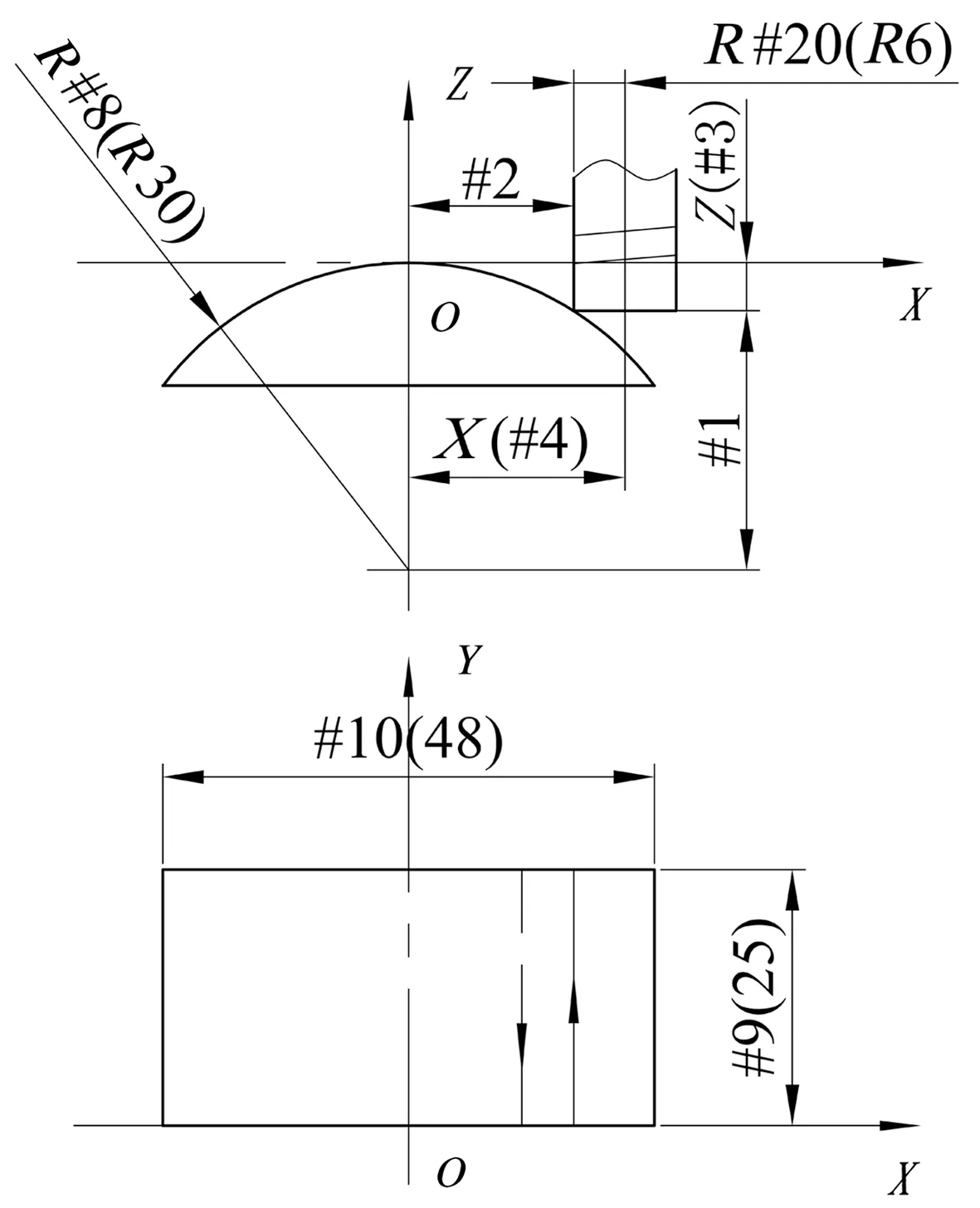
图4 旋转前的数学模型
2.3 数学模型
#1:刀具底面到圆弧中心的距离;
#2:刀刃到圆弧对称中心的距离;
#3:Z坐标值;
#4:X坐标值;
#8:圆弧半径;
#9:圆弧面的长度;
#10:圆弧面的宽度;
#11:圆弧面的深度;
#18:旋转角度;
#20:刀具半径。
2.4 加工程序



图5 旋转后的数学模型

3 结语
通过以上宏程序加工圆弧面的例子,得出第二个程序具有以下三个优点。
(1)用变量的形式对参数赋值,通用性较强,具有独特的作用[2]。例如圆弧面的尺寸、旋转角度发生改变,只需给这些参数赋值,完全可以用同一个程序来加工。
(2)在加工中用沿Y 向往复走刀的方法,大大减少了单一方向运动中需要抬刀的步骤,节约了加工时间,大大提高了加工效率。
(3)程序虽然采用刀具中心轨迹编程,但当刀具直径发生变化时(刀具磨损或者更换新刀),只要对直径重新赋值,而不需修改程序的其他地方,起到了类似刀具半径补偿功能的作用。
[1]陈海舟.数控铣削加工宏程序及应用实例[M].北京:机械工业出版社,2008.
[2]黄冬英.宏程序在刻线加工中的应用[J].制造技术与机床,2011(2):160-162.

