GPU acceleration of a nonhydrostatic model for the internal solitary waves simulation*

CHEN Tong-qing (陈同庆), ZHANG Qing-he (张庆河)

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China, E-mail: coastlab@163.com

GPU acceleration of a nonhydrostatic model for the internal solitary waves simulation*

CHEN Tong-qing (陈同庆), ZHANG Qing-he (张庆河)

State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China, E-mail: coastlab@163.com

(Received May 21, 2012, Revised September 10, 2012)

The parallel computing algorithm for a nonhydrostatic model on one or multiple Graphic Processing Units (GPUs) for the simulation of internal solitary waves is presented and discussed. The computational efficiency of the GPU scheme is analyzed by a series of numerical experiments, including an ideal case and the field scale simulations, performed on the workstation and the supercomputer system. The calculated results show that the speedup of the developed GPU-based parallel computing scheme, compared to the implementation on a single CPU core, increases with the number of computational grid cells, and the speedup can increase quasilinearly with respect to the number of involved GPUs for the problem with relatively large number of grid cells within 32 GPUs.

Graphic Processing Unit (GPU), internal solitary wave, nonhydrostatic model, speedup, Message Passing Interface (MPI)

Introduction

The internal solitary waves are frequently observed in oceans in the world. These waves may have amplitudes larger than one hundred meters below the water surface and cause a strong underwater current[1], which can greatly impact the offshore structures as well as the ocean environment[2-4]. Therefore, the internal solitary wave has attracted more and more research attention. In recent years, the nonhydrostatic model has been extensively employed as an efficient tool to investigate the generation and evolution processes of the internal solitary waves[5]. However, the high computational cost in numerically solving the pressure Poisson equation for the nonhydrostatic model has limited its use in large scale systems. Therefore, it is of great importance to improve the computational efficiency of solving the pressure Poisson equation.

The parallel computation on the cluster of CPUs connected by a fast network has been used to accelerate the calculation related with most of the nonhydrostatic ocean models. Nevertheless, the CPU is not the only processing unit in the computer system. The Graphic Processing Unit (GPU), initially used for rendering images, has turned into a highly parallel device. With the many-core architecture, it is suitable for data-parallel computations. In 2007, NVIDIA released the Compute Unified Device Architecture (CUDA)[6], including the hardware specifications and the programming environment, which greatly facilitates the parallel programming on the GPU. The CUDA has been used in the applications of computational fluid dynamics. For example, Asouti et al.[7]and Zaspel and Griebel[8]presented Navier-Stokes solvers based on CUDA using the finite volume method and the finite difference method, respectively. Herault et al.[]and Wang and Liu[10]simulated the free surface flow on the GPU using the Smoothed Particle Hydrodynamics (SPH) method. Bleichrodt et al.[11]presented an efficient solution for the two dimensional barotropic vorticity equation of an ocean model on a GPU.

According to the successful applications mentioned above and the rapid development of GPU technologies, the computational efficiency of the nonhydrostatic model is likely to be improved by meansof the GPU. So, accelerating a nonhydrostatic model through the GPU is explored to simulate the internal solitary wave in the present study. The remainder of this paper is organized as follows. In Section 1, the governing equations are briefly introduced. The implementation method using the GPU is described in Section 2. In Section 3, the simulated results are presented and the performance of the scheme is discussed, followed by summaries in Section 4.

1. Governing equations

In the present study, the three-dimensional nonhydrostatic ocean model, Stanford Unstructured Nonhydrostatic Terrain-following Adaptive Navier-Stokes Simulator (SUNTANS), is employed. More details about the model can be found in Ref.[12]. We just briefly list the governing equations in this section.

whereu,vandw are the velocity components in thex,yandz directions,uis the velocity in vector form,qis the nonhydrostatic pressure, and fis the Coriolis parameter. The free surface elevation is given byh, which is obtained by the solution of the following equation

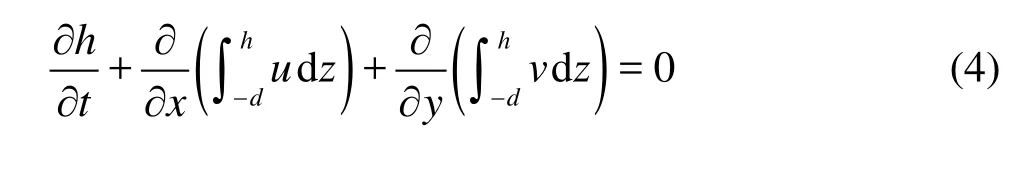
The total water density is given by ρ0+ρ, whereρ0is the constant reference density. The water density can be obtained by the ocean state equation, where the density is a function of pressure, temperature and salinity. The baroclinic pressure headrin Eq.(1) and Eq.(2) is given by

The nonhydrostatic pressure is obtained through solving the pressure Poisson equation. The temperature and the salinity are obtained from the corresponding convection-diffusion equation.

The SUNTANS model employs the unstructured triangular grid in the horizontal plane and the multilayered z-level grid in the vertical direction, and the governing equations are discretized based on the finite volume method. The free surface and vertical diffusion terms are solved semi-implicitly. The explicit terms are discretized with the second order Adams-Bashforth method. The details of the numerical discretization and the algorithms for the model are in Fringer et al.[12].

2. Implementation method

In the simulation of the internal solitary waves using the SUNTANS model, about 75%-95% of the computation time is spent on the iterative solution of the Poisson equation of the pressure. Therefore, in order to accelerate the computation, the CUBLAS[13]and CUSPARSE[14]libraries of CUDA 4.0 are employed to solve this equation on the GPUs. The other parts of the model are still processed by the CPU. The CUBLAS library contains a set of basic linear algebra subroutines for matrix and vector computations, and the CUSPARSE library provides similar subroutines for sparse matrices and vectors.

2.1 Matrix storage

The discretized Poisson equation of the pressure can be written as the following linear equations[12]

whereA is the coefficient matrix,xis the unknown vector of the pressure, andbis the right-hand side vector. The matrix in Eq.(6) is a symmetric positive definite matrix and it is usually a large sparse matrix with a large number of zero elements. In order to reduce the memory usage, special storage formats of the matrix are required. Two kinds of compressed formats are currently supported by the CUSPARSE library, i.e., the Compressed Sparse Row (CSR) format and the Compressed Sparse Column (CSC) format. The CSR format is adopted in this paper. For example, an 4×5matrix[14]

can be stored in CSR format as

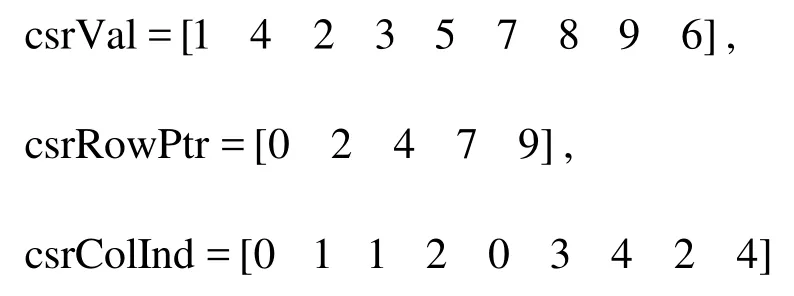
where csrValcontains the non-zero elements in the matrix, stored row by row,csrRowPtris used to store the number of non-zero elements in every row of the matrix, with the difference betweencsrRowPtr( i +1)and csrRowPtr(i)representing the number of non-zero elements in theithrow, starting from the zeroth row;csrColIndholds the column indices of the corresponding elements incsrVal, starting from the zeroth column.

2.2 Parallel scheme

In the SUNTANS model, Eq.(6) can be solved by the conjugate gradient algorithm, which is one of the well known iterative numerical methods for solving sparse symmetric positive definite linear systems as shown in Eq.(6). The conjugate gradient algorithm is as follows.

Suppose x0is the initial value of the unknown vector, and letp 0=r0=b-Ax0. Fork∈N, the kth iteration is

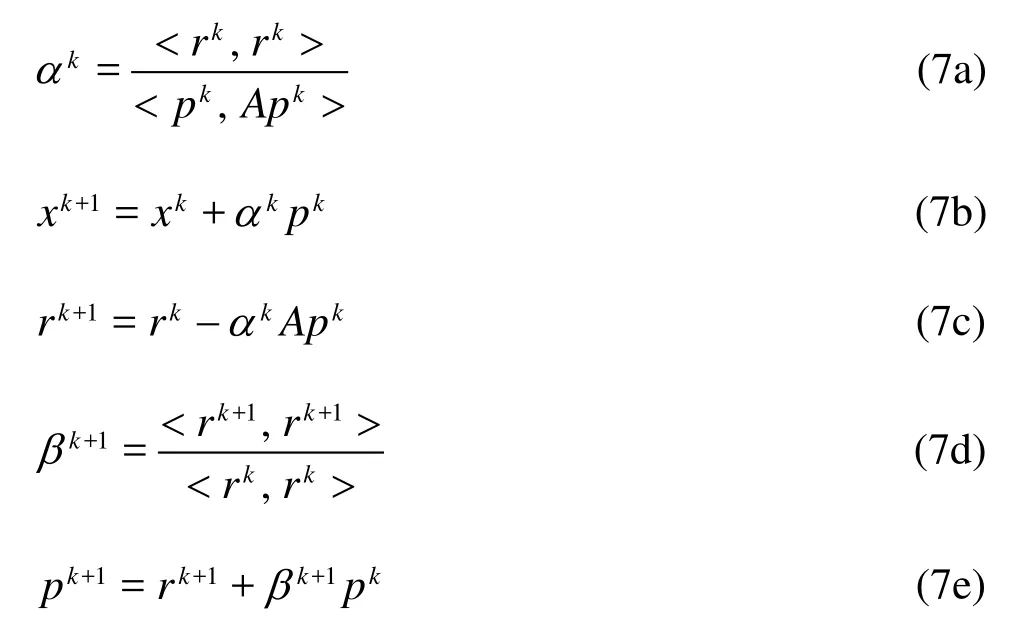
where ＜·, ·＞indicates the inner product of two vectors. The above algorithm requires only operations about vectors and matrices, which can be found in the CUBLAS and CUSPARSE libraries.

Generally speaking, the computing nodes, connected by a fast network, are currently equipped with one or two GPUs at the center of supercomputing. The desktop level computer usually has one GPU on the motherboard. In order to offer the universality of the scheme, the GPU-based implementation should be able to be used not only on the single computer system but also on the supercomputer with GPUs distributed in different computing nodes. Therefore, two kinds of parallel schemes are developed, i.e., the single GPU scheme and the multiple GPUs scheme. For the single GPU scheme, Eq.(6) is solved on a single GPU, and the operation on the GPU is invoked by the CPU process. For the multiple GPUs scheme, the computational domain is decomposed into different subdomains. Every subdomain is distributed to a GPU and a corresponding CPU core. Equation (6) is solved using multiple GPUs, and the operation on every GPU is invoked by the corresponding CPU process, which is similar to the single GPU scheme. The data communication across the GPUs is realized through CPUs. The data are firstly transferred from GPU to CPU using the CUDA Application Programming Interface (API) and then exchanged between the corresponding CPUs by the Message Passing Interface (MPI) functions.

The detailed multiple GPUs scheme is as follows:

In the above algorithm, the variables with subscript gare relevant to the whole computational domain, and those without this subscript are associated with the subdomain. In order to exchange data between the subdomains, the overlapped cells at the interface are utilized to receive the data from the neighboring subdomain, as illustrated in Fig.1. The single GPU scheme is similar to the above multiple GPUs scheme except for the data exchange process, which is not required.

Fig.1 Schematic diagram of the domain partition and data exchange

Fig.2 Schematic diagram of the computational domain of the ridge case

3. Results and discussions

3.1 Application on the workstation

The numerical simulations of the internal solitary wave were carried out on a single workstation, equipped with two CPUs and four CUDA-enabled GPUs. The key properties of the CPU and GPU are as follows:

(1) CPU: Intel Xeon E5620, 2.40GHz, 4 Cores, 12MB Cache.

(2) GPU: NVIDIA Tesla C2070, 1.15GHz, 448 CUDA Cores, 6GB GDDR5 Memory.

All the computations both on the CPU and the GPU are performed in double precision for better computation accuracy. The Error Checking and Correcting (ECC) protected calculation is applied for the execution on the GPU, although this may make the memory bandwidth reduced by at least 8%[8].

3.1.1 Comparison of the results by CPU and GPU implementations

The simulated results by the CPU and GPU implementations for a two-dimensional numerical experiment are compared to validate the computation precision of the developed GPU scheme. The computational domain (as shown in Fig.2) is 400 km in length, and the water depth is 800 m. A ridge is located at the center of the computational domain. The ridge height is given by Eq.(8), where x0represents the coordinate of the ridge center in thex direction,hmis the maximum height andLis the scale width of the ridge. The model is forced by the M2current,umsin(ω t), on the left and right boundaries, whereumis the maximum velocity.

A linear equation of state is used as

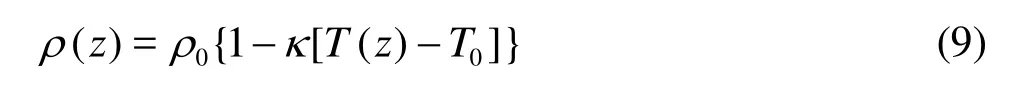
whereρ0and T0are the reference density and temperature, andκis the thermal expansion coefficient. The initial temperature is given as

whereΔρis the density scale, and z0and Dare the center position and the thickness of the thermocline, respectively. The values of the parameters used in the computations are listed in Table 1.

Figure 3(a) shows the simulated results of the internal solitary waves at 37.26 h by the CPU implementation. Only the results in the upper 300 m are given for clarity. The maximum relative difference,Emax, per vertical layer of the results by CPU and multiple GPUs algorithms is shown in Fig.3(b), whereIrepresents the index of vertical layer. It can be seen that the results obtained by the GPU implementation are nearly the same as those obtained by the CPU solver. In the whole computational domain, the maximum relative difference between the results obtained by the GPU a

nd CPU imp lementati ons is les s than 3×10-5, whichisacceptablebecausetheGPUonlysupports64-bit operations for the double precision calculations, while it is 80-bit on the CPU. In Fig.3(a), the spikelike waves are the internal solitary waves, originating from the interaction between the tidal current and the bottom topography of the ridge and propagating in two directions.

Table 1 Parameters used in the ridge case

Fig.3 Simulated results of internal solitary waves obtained by the CPU solver and the maximum relative error per vertical layer obtained by the GPU implementation

Fig.4 Speedup of the GPU scheme at different numbers of grid cells

3.1.2 Speedup analysis of the GPU algorithm

The above problem is used to evaluate the efficiency of the developed GPU algorithm. All the following calculations use the same setup, and all the simulations terminate after 1 000 time steps. The computation time is employed to indicate the efficiency of the GPU algorithm. It is noted that the computation time used in the following analysis is the total time spent on the model run, containing the solution of the pressure Poisson equation and other parts of the model.

Figure 4 shows the speedup of the GPU scheme at different numbers of grid cells,Nc. The speedup, Sp, is defined as the ratio of the computation time on a single CPU core to that consumed by the GPU implementation. In Fig.4, “1CPU+1GPU” represents the computation by the single GPU scheme, and “4CPU+ 4GPU” means the computation by the multiple GPUs scheme on four GPUs. It is found that the computations with four GPUs are generally faster than the counterpart with only one GPU. However, for the case with fewer grid cells (for example, 5×104cells), the computation with four GPUs is slightly slower than that with only one GPU. When the problem size is smaller, the ratio of computation time to communication time becomes smaller for the case with more GPUs, therefore, relatively more time is spent on data communication, which leads to longer time for the total execution. It is noted that the number of three-dimensional grid cells is usually larger than 5×104in the simulation of internal solitary waves for a certain ocean area, and the saving of computational time by using more GPUs may become significant. In Fig.4, it can also be seen that the speedup depends on the number of grid cells and GPUs employed in the simulation. The speedup increases with the number of grid cells and it increases more quickly for the case with more GPUs.

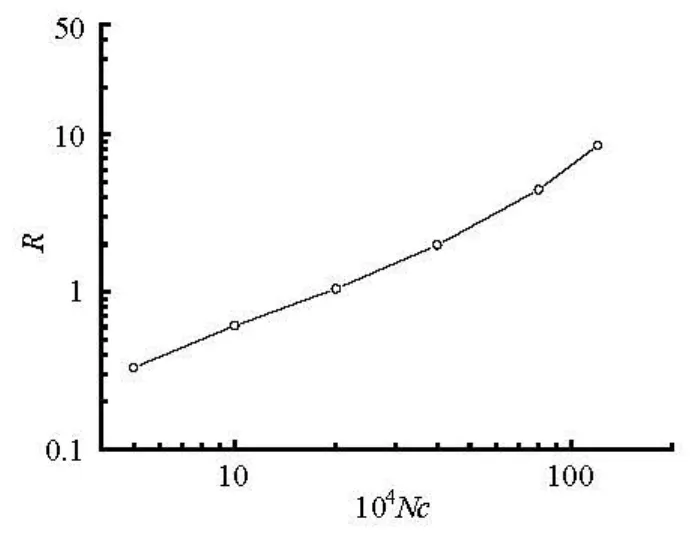
Fig.5 Ratio of the computation time on 4 CPU cores to that by 4 GPUs

Figure 5 presents the ratio,R, of the computation time on four CPU cores to that by four GPUs. It is found that the computations with four GPUs are faster than the counterpart with four CPU cores for the cases with more grid cells. However, for the case with fewer grid cells, the computation with four GPUs is slower than that with four CPU cores. It spends relatively more time on data exchange between GPU memory and CPU memory for the case with fewer grid cells, which makes the computation efficiency by four GPUs lower than that by four CPU cores.

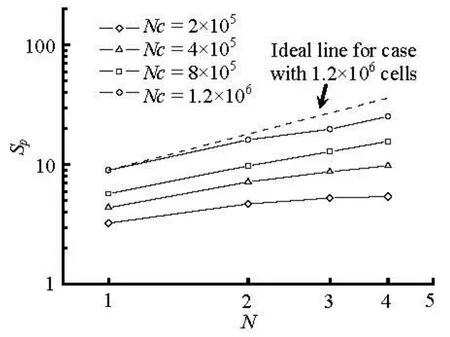
Fig.6 Speedup of the GPU scheme for different numbers of GPUs

In Fig.6, the relationship between the speedup, Spand the number of GPUs is given for different numbers of grid cells. It can be seen that the speedup increases with the number of GPUs, especially in the case with more grid cells. For the case with 1.2×106three-dimensional grid cells, the speedup of 25.4 times is achieved using four GPUs. In addition, the speedup can increase quasi-linearly with respect to the number of GPUs for the problem with more grid cells within four GPUs. The dashed line in Fig.6 indicates the ideal scalability for the case with 1.2×106cells, i.e., the speedup by n GPUs is n times of that by one GPU. Since only four CUDA-enabled GPUs are equipped in the used workstation, the application of the developed GPU scheme with more GPUs on the supercomputer is presented below.

3.2 Application on the supercomputer

To examine the performance of the developed GPU scheme on supercomputers, the simulations were carried out on the Chinese Tianhe-1A system[15,16]. The key properties of the CPU and GPU on Tianhe-1A are listed as follows:

(1) CPU: Intel Xeon X5670, 2.93GHz, 6 Cores, 12MB Cache.

(2) GPU: NVIDIA Tesla M2050, 1.15GHz, 448 CUDA Cores, 3GB GDDR5 Memory.

The developed GPU scheme is applied for the simulation of internal solitary waves in the northeastern South China Sea. The computational domain (as shown in Fig.8) is about 930 km in length and 540 km in width. The total number of three-dimensional grid cells is about 1.2×107. The size of the horizontal grid cell is about 4 km near the open boundaries and 1 km near the islands. In the vertical direction, 100 layers are used with the minimum height of 12 m near the surface. The time step is chosen as 15 s. At the open boundaries, the model is forced by the tidal velocity components obtained from the regional solution (China Sea 2010) of the OTIS tidal model[17]. The initial vertical distributions of temperature,T , and salinity,S , are shown in Fig.7. The simulation is performed over the period from 18 to 21 June 2005. In Fig.8, the simulated temperature at the depth of about 100 m is presented. The dark lines in Fig.8 indicate where the internal solitary waves of depression type have propagated to.

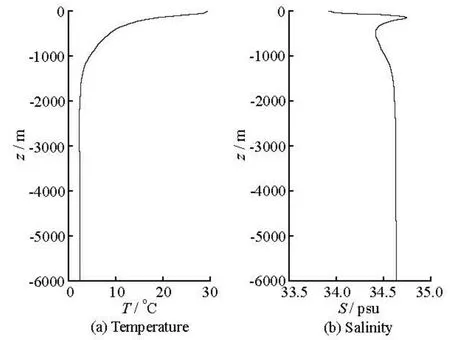
Fig.7 Initial vertical distributions of temperature and salinity

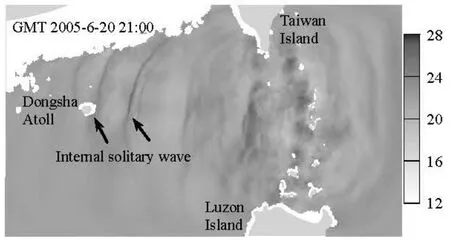
Fig.8 Simulated temperature in the northeastern South China Sea by the GPU implementation

To examine the scalability of the GPU scheme on supercomputers, a series of simulations are carried out on Tianhe-1A using different numbers of GPUs. Figure 9 depicts the speedup achieved with different numbers of GPUs. The speedup is also calculated as the ratio of the computation time on a single CPU core to that consumed by the GPU implementation. It is found that the speedup can increase quasi-linearly with respect to the number of GPUs within 32 GPUs. The dashed line in Fig.9 shows the ideal scalability,i.e., the speedup byn GPUs isntimes of that by one GPU. The computation on Tianhe-1A with 4 GPUs is also compared to that on the dual CPU workstation with 4 GPUs used in Section 3.1. The ratio of the computation time on the workstation to that on Tianhe-1A is about 1.1, which means the computation on Tianhe-1A is slightly faster than that on the workstation. Although the GPUs are distributed on different computing nodes on the Tianhe-1A system, the computing nodes are connected by a kind of high performance network. The data communication for the computation on the workstation is also realized through the MPI functions. And the time spent on the data communication is usually less than 2% of the total computation time for the 4 GPUs case. In addition, the performance of the CPU on Tianhe-1A is better than that on the workstation. Hence, the computation efficiency on Tianhe-1A is slightly higher.

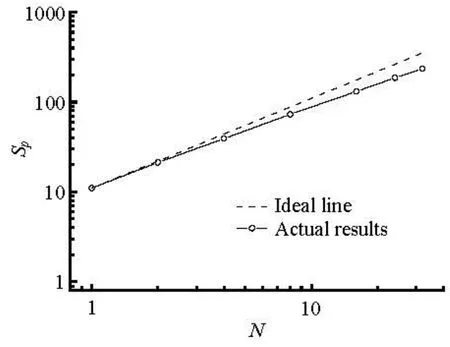
Fig.9 Speedup of the GPU scheme for different numbers of GPUs

4. Conclusions

The GPU-based implementation of a nonhydrostatic model for the simulation of internal solitary waves is presented and discussed. The most time-consuming part of the nonhydrostatic model, i.e., the iterative solution of the pressure Poisson equation, is ported from CPU to GPU based on CUDA, and a single GPU algorithm and a multiple GPUs algorithm are developed for different computer systems.

The results of numerical tests indicate that the precision of the developed GPU scheme is the same as that of the CPU scheme. The computational efficiency of the GPU scheme is analyzed by a series of numerical experiments, including an ideal case and the field scale simulations, performed on the workstation and the supercomputer system. It is found that the speedup of the GPU scheme, compared to the single CPU core execution, is generally proportional to the number of grid cells and GPUs employed in the simulation. For the problem with more grid cells, the speedup can increase quasi-linearly with respect to the number of GPUs within 32 GPUs, which demonstrates good scalability of the developed scheme.

Acknowledgements

The authors gratefully appreciate Dr. Oliver Fringer for providing the original codes of the SUNTANS model and two anonymous reviewers for their helpful suggestions. The calculations for South China Sea were performed on the Tianhe-1A system. The authors thank the support of the National Supercomputer Center in Tianjin, China.

[1] RAMP S. R., YANG Y. J. and BAHR F. L. Characterizing the nonlinear internal wave climate in the northeastern South China Sea[J]. Nonlinear Processes in Geo- physics, 2010, 17(5): 481-498.

[2] BOLE J. B., EBBESMEYER C. C. and ROMEA R. D. Soliton currents in the South China Sea: Measurements and theoretical modeling[C]. Proceedings of the 26th Annual Offshore Technology Conference. Houston, USA, 1994, 367-376.

[3] SONG Z. J., TENG B. and GOU Y. et al. Comparisons of internal solitary wave and surface wave actions on marine structures and their responses[J]. Applied Ocean Research, 2011, 33(2): 120-129.

[4] REEDER D. B., MA B. B. and YANG Y. J. Very large subaqueous sand dunes on the upper continental slope in the South China Sea generated by episodic, shoaling deep-water internal solitary waves[J]. Marine Geology, 2011, 279(1-4): 12-18.

[5] LI Qun, XU Zhao-ting. A nonhydrostatic numerical model for density stratified flow and its applications[J]. Journal of Hydrodynamics, 2008, 20(6): 706-712.

[6] KIRK D. B., HWU W. W. Programming massively parallel processors: A hands-on approach[M]. Burlington, Canada: Elsevier, 2010.

[7] ASOUTI V. G., TROMPOUKIS X. S. and KAMPOLIS I. C. et al. Unsteady CFD computations using vertexcentered finite volumes for unstructured grids on Graphics Processing Units[J]. International Journal for Numerical Methods in Fluids, 2011, 67(2): 232-246.

[8] ZASPEL P., GRIEBEL M. Solving incompressible twophase flows on multi-GPU clusters[J]. Computers and Fluids, 2013, 80: 356-364.

[9] HERAULT A., BILOTTA G. and DALRYMPLE R. A. SPH on GPU with CUDA[J]. Journal of Hydraulic Research, 2010, 48(Suppl.): 74-79.

[10] WANG Ben-long, LIU Hua. Application of SPH method on free surface flows on GPU[J]. Journal of Hydro- dynamics, 2010, 22(5Suppl.): 912-914.

[11] BLEICHRODT F., BISSELING R. H. and DIJKSTRA H. A. Accelerating a barotropic ocean model using a GPU[J]. Ocean Modelling, 2012, 41: 16-21.

[12] FRINGER O. B., GERRITSEN M. and STREET R. L. An unstructured-grid, finite-volume, nonhydrostatic, parallel coastal ocean simulator[J]. Ocean Modelling, 2006, 14(3-4): 139-173.

[13] NVIDIA CORPORATION. CUDA CUBLAS library[R]. Report No. PG-05326-040 V01, NVIDIA Corporation, Santa Clara, USA, 2011.

[14] NVIDIA CORPORATION. CUDA CUSPARSE library[R]. Report No. PG-05329-040 V01, NVIDIA Corpo- ration, Santa Clara, USA, 2011.

[15] YANG Xue-Jun, LIAO Xiang-Ke and LU Kai et al. The Tianhe-1A supercomputer: Its hardware and software[J].Journal of Computer Science and Technology, 2011, 26(3): 344-351.

[16] LU F., SONG J. and YIN F. et al. Performance evaluation of hybrid programming patterns for large CPU/ GPU heterogeneous clusters[J]. Computer Physics Communications, 2012, 183(6): 1172-1181.

[17] EGBERT G. D., EROFEEVA S. Y. Efficient iverse modeling of barotropic ocean tides[J]. Journal of Atmospheric and Oceanic Technology, 2002, 19(2): 183-204.

10.1016/S1001-6058(11)60374-1

* Project supported by the Natural Science Foundation of Tianjin, China (Grant No. 12JCZDJC30200), the National Natural Science Foundation of China (Grant No. 51021004) and the Fundamental Research Fund for the Central Nonprofit Research Institutes of China (Grant No. TKS100206).

Biography: CHEN Tong-qing (1980-), Male, Ph. D. Candidate

ZHANG Qing-he, E-mail: coastlab@163.com