城区公路选址的优化模型
刘冬华,邓俊谦,郭琼琼
(郑州铁路职业技术学院,河南 郑州 450052)
1 问题的提出与分析
某区政府在图1所示的区域修建一条从A到B的直线型公路,由于涉及到路面拆迁等因素,各地段建设费用有所不同,图1中的数字代表区域公路单位建设费用(单位:百万元).未标明数字的任何地方单位建设费用均为1;每个网格边界上的费用按该地区最小单位费用计算.图1中每个网格长与宽都为1个单位.要解决的问题是:按建设部门的如下具体要求,从建设费用最省的角度,给出最优方案:
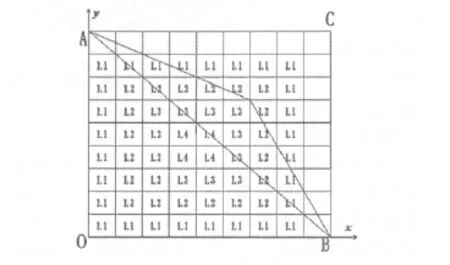
图1 区域内公路单位建设费用
(1)公路至多只能有1个转弯点,且转弯点只能建在图1中所示的网格点上.
(2)公路至多可以有2个转弯点,且转弯点只能建在图1中所示的网格点上.
从图1可以看出,线段AB左下侧中各小区域的单位建设费用均大于右上侧中对称小区域的单位建设费用,所以,要使从A到B的直线型公路的建设费用最省,转弯点应该选AB的右上侧区域.
对于所要解决的问题1和问题2,由于要求转弯点只能建在网格点上,因此,求解的思路是:首先,设出转弯点的坐标并表示出各公路段的直线方程,然后求出网格线与各公路段的交点坐标,并表示出从A到B的总建设费用,其次,利用Matlab编程,分别计算出转弯点取遍各网格点时的总建设费用,从中筛选出使总建设费用最小的转弯点.
为了建立建设费用的最优化模型,根据问题所给的条件及实际公路建设的一般原则作出如下假设:
(1)图1中各小区域的单位建设费用是真实可靠的;
(2)每个区域的建设费用只与该区域的公路长度和单位建设费用有关,不考虑意外损坏等其他相关费用;
(3)对于有两个转弯点的公路,建设的直线型公路段为:A→左转弯点→右转弯点→B.
2 问题1的模型建立与求解
问题1要求至多有一个转弯点,所以可以分没有转弯点和恰好有一个转弯点两种情况来计算总建设费用.显然,没有转弯点时,公路AB的建设费用为

下面来讨论恰好有一个转弯点时的建设费用.
观察图1所示各网格区域的单位建设费,可以看出:线段AB左下侧中各小区域的单位建设费用均大于右上侧中对称小区域的单位建设费用,且所有区域上的数值关于y=x对称.因此,设直线型公路的唯一转弯点P在AB右上侧的网格点上,坐标为(m,n),公路PA→PB的总建设费用为Z,并且用反证法易证下面的引理.
引理 若P(m,n)是使总建设费用最省的转弯点,则P关于y=x的对称点P'(n,m)也一定是使总建设费用最省的转弯点.
根据引理,我们只需求出其中一个,即可利用对称性得到第二个.
将公路段PA、PB与各网格线的交点按横坐标由小到大排序,坐标依次记为(xi,yi)(i=1,…,N,其中N为交点的个数).这些交点将公路分成N-1个小公路段,第i个小公路段的左端点记为(xi,yi),长度记为li(i=1,…,N-1),其所对应的网格区域用右上角网格点的坐标标记,记为(gxi,gyi)(i=1,…,N -1).并且
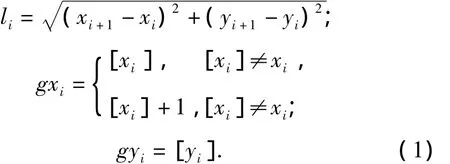
记图1中各小区域的单位建设费用为cij(i=1,…,9,j=1,…,9,分别为相应区域右上角网格点的坐标).下面分四种情形,表示公路的总建设费用.
情形1 转弯点P在网格点C
此时,总建设费用为Z=18.显然,该建设费用大于没有转弯点时的建设费用,因此,舍去这种情形.
情形2 转弯点在线段AC上的网格点且不同于点C

其中cgxi,gyi为公路段PB被图1中网格线所分成的第i个小公路段所在网格区域的单位建设费用;li、gxi、gyi的意义与式(1)相同.
情形3 转弯点P在线段BC上的网格点且不同于点C
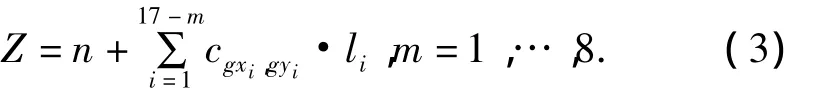
其中cgxi,gyi为公路段PA被图1中网格线所分成的第i个小公路段所在网格区域的单位建设费用;li、gxi、gyi的意义与式(1)相同.
情形4 P既不在线段AC又不在BC上的网格点
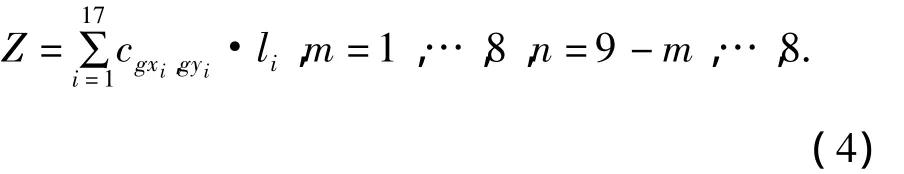
其中cgxi,gyi为公路段PA和PB被图1中网格线所分成的第i个小公路段所在网格区域的单位建设费用;li、gxi、gyi的意义与式(1)相同.
以直达公路AB的建设费用14.9907百万元为总建设费用的初始值,根据式(1)~(4),利用MATLAB编程计算转弯点在不同网格点上时,公路的总建设费用,并比较它们的大小,求出最小建设费用,此时所对应的转弯点即为最优设计方案的转弯点.运行所编程序,得转弯点为P(6,5)时最小总建设费用Z=14.7068.结合引理1可知:使得总建设费用最少的转弯点为点(6,5)或点(5,6),最小总建设费用为14.7068百万元.建设费用最省的公路设计方案如图2所示.
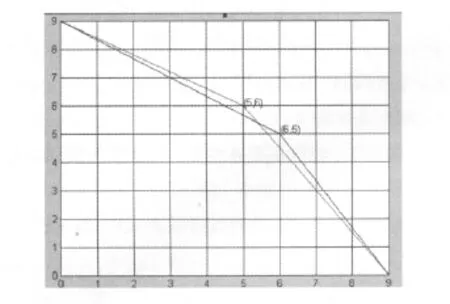
图2 问题1的最优设计方案
3 问题2的模型建立与求解
问题2要求至多有两个转弯点,即分为两种情形:至多有一个转弯点(即问题1的情形)和恰好有两个转弯点.因此,我们只需再研究:恰有两个转弯点时的最优设计方案,并将其最小建设费用与问题1的最小总建设费用比较,两者中最小值即为问题2的最小建设费用,所对应的设计方案即为问题2的最优设计方案.
根据假设(3),设左转弯点为P1(m,n),右转弯点为 P2(s,q),其中 m <s,且 P1、P2均在 AB 右上侧的网格点上.与问题1的方法类似,下面分情形来讨论恰有两个转弯点时的总建设费用.
情形1 P1在AC上、P2在BC上
此时,P1A的建设费用为m,P2B的建设费用为q.P1P2的直线方程为,用与前面相似的方法,可得 P1P2得的建设费用为
cgxi,gyi·li.于是,公路的总建设费用为
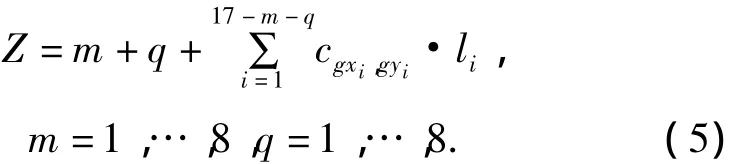
其中 li、gxi、gyi的意义与式(1)相同.
情形2 P1在AC上、P2不在BC上
此时,P1A的建设费用为m,P1P2的方程为y=,P2B的方程为.相似的方法可以求出公路段P1P2和P2B的建设费用.于是,可得公路的总建设费用为
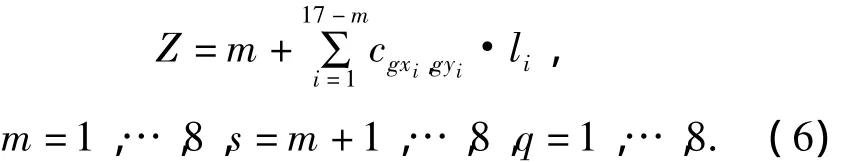
其中 li、gxi、gyi的意义与式(1)相同.
情形3 P1不在AC上、P2在BC上
这种情形下,P2B的建设费用为q,P1A的方程为.用与前面相同的方法可求出公路段P1A的建设费用为
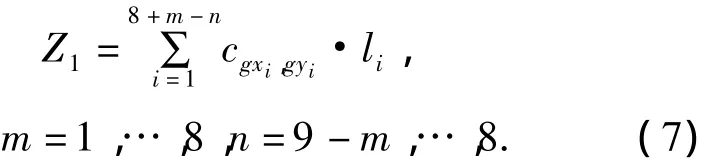
其中 li、gxi、gyi的意义与式(1)相同.
公路段P1P2的建设费用,要分两种情况来求.当n≠q时,P1P2的方程为,用与前面相同的方法可求出公路段P1P2的建设费用.当n=q时,P1P2在网格线上,单位建设费用应取该地区最小单位费用,根据题意和图1中的数据特点,这时,应取 gxi=[xi]+1,gyi=[yi]+1.于是,公路段P1P2的建设费用为其中当n≠q时,gxi,gyi的表达式与式(1)相同;当n=q时,gxi=[xi]+1,gyi=[yi]+1.

综上所述,在情形3下,公路的总建设费用为

情形4 P1不在AC上、P2也不在BC上
这种情形下,P1A的方程为,用与前面相同的方法可得P1A的建设费用Z1与式(7)相同.P2B的方程为,类似的方法可得P2B的建设费用为P1P2的方程为的建设费用需分三种情形来求.
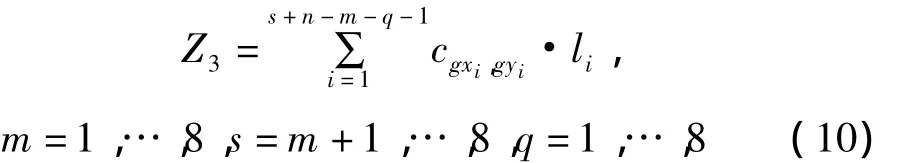
(1)当n>q时,用与前面相同的方法可得P1P2的建设费用为其中 li、gxi、gyi的意义与式(1)相同.

(2)当n=q时,用与情形3相似的方法,可得P1P2的建设费用为
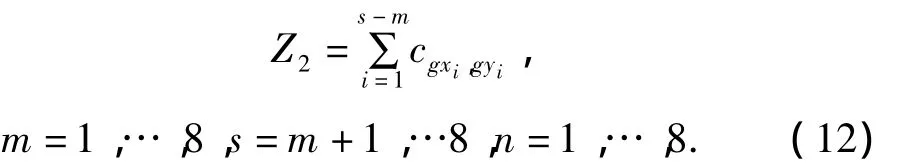
其中 gxi=[xi]+1,gyi=[yi]+1.
(3)当n<q时,线段P1P2是上升的,此时,应取gxi=[xi+1],gyi=[yi+1].于是,公路段 P1P2的建设费用为

其中 gxi=[xi+1],gyi=[yi+1].
综上所述,在情形4下,公路的总建设费用为

根据式(5)~(14),利用MATLAB编程计算:两转弯点在不同网格点上时,公路的总建设费用,并比较它们的大小,求出最小建设费用及所对应的转弯点.运行所编程序,得两转弯点分别为(7,4)和(4,7),最小建设费用为14.6241.显然,这个建设费用小于问题1中所求的最小建设费用,因此,对于问题2,建设费用最省时的转弯点分别为(7,4)和(4,7)(公路的最优设计方案如图3所示),此时的最小建设费用为14.6241.
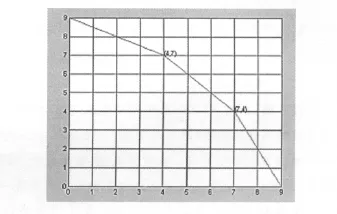
图3 问题2的最优设计方案
4 模型的评价与改进方向
本文建立了转弯点均在网格点上,并且至多有一个转弯点或至多有两个转弯点情形下,使得城区公路的建设费用最省的最优设计模型,并利用广度搜索方法和Matlab软件编程,求出了两种情形下的最优设计方案,对于实际的生产建设具有较好的指导意义.
在实际生产建设中,转弯点还可以在网格线或区域的任何位置上.因此,我们还可以继续研究下列情形下的最优设计方案:
(1)公路至多只能有2个转弯点,且转弯点只能建在图1中所示的网格线上.
(2)公路至多只能有2个转弯点,且转弯点只能建在图1中所示区域的任何位置上.
[1]韩中庚.数学建模实用教程[M].北京:高等教育出版社,2012.
[2]费浦生.数学建模及其基础知识详解[M].武汉:武汉大学出版社,2006.

