同步误差下OFDM稀疏信道估计

王小舟, 张 严, 胡友峰



同步误差下OFDM稀疏信道估计

王小舟, 张 严, 胡友峰

(中国船舶重工集团公司 第705研究所昆明分部, 云南 昆明, 650118)

在实际正交频分复用(OFDM)水声通信中, 当直达声能量较弱时, 存在较大的同步误差, 导致梳状导频最小二乘信道估计出现混叠。在分析了同步误差对最小二乘(LS)信道估计算法影响的基础上, 提出了一种在同步误差下可稳定工作的OFDM稀疏信道估计算法, 并建立了稀疏信号重构的模型。该方法将存在同步误差时的信道估计认为是通过不完整频域采样重构稀疏信号的问题, 利用压缩感知算法进行信道估计。在同步误差严重的情况下, 可以取得较好的信道估计效果, 从而降低误码率。湖试试验验证了该方法的有效性。

水声通信; 正交频分复用; 稀疏信道估计; 同步误差; 压缩感知

0 引言

水声通信技术在众多领域都有良好的应用前景, 得到了广泛关注。但是水声信道, 尤其是浅水信道, 由于带宽有限、多途严重等问题, 给高速率通信带来了很大难度。近年来, 正交频分复用(orthogonal frequency division multiplexing, OFDM)通信方式在高速率水声通信领域取得了较好的成果[1]。OFDM相对于单载波通信方式最显著的优势就是通过离散傅里叶变换(discrete fourier transforms, DFT)消除了多途带来的码间干扰问题, 简化了均衡过程。

OFDM通信的重要环节是信道估计。近年来,有关学者对此做了大量研究。虽然水声信道中多径时延扩展严重, 但是路径的个数有限, 这就构成了水声信道的稀疏特性。文献[2]中假设信道冲击响应只存在于接收信号后的一段时间之内, 利用梳状导频对这段时间中的信道进行最小二乘估计, 并在之后进行补零。文献[3]提出一种迭代更新的信道估计算法, 利用解调出的码元进行当前信道估计, 将小于某阈值的信道响应认定为噪声, 设为0, 和上一次的信道估计进行加权平均。文献[4]将信道的稀疏性扩展到多普勒时延平面, 利用压缩感知技术对多普勒时延平面中的稀疏抽头进行估计。此方法解决了由多普勒扩展所造成的载波间干扰(inter-carrier interference , ICI)问题。

在实际水声通信过程中同步误差会对不同的信道估计产生不同的影响。在信道已知并不考虑OFDM符号间干扰(inter-symbol interference, ISI)的情况下, 可以证明同步误差造成的影响等价于信道的循环平移, 这可能破坏信道估计的稀疏假设。同步误差对类似文献[2]中的梳状导频算法会产生明显的混叠, 导致均衡效果明显下降,但对块状导频算法影响较小。

针对同步误差, 希望在不对信道长度做出假设的前提下, 用少量的导频对循环平移的信道进行完整估计。利用信道的稀疏特性, 可以证明这等价于文献[5]中描述的通过不完整的频域信息对原始稀疏信号进行重构的问题。设计伪随机分布的导频信号, 满足了文献[5]中给出的重构条件。通过建立凸优化模型, 利用压缩感知算法迭代求解。不同于文献[4]和文献[6]提出的等间隔导频压缩感知算法, 伪随机分布的导频可以使信道估计长度达到OFDM符号长度而不产生混叠。

为了减少压缩感知信道估计中的噪声, 使用文献[3]中的迭代方法对估计信道进行平滑, 可以进一步改进估计效果。

本文介绍了一种基本的OFDM水声通信方法, 分析了同步误差对导频信道估计的影响, 并提出一种压缩感知算法以解决上述问题, 湖试试验验证了该方法的有效性。

1 OFDM系统与信道估计

假设OFDM有个子载波, 其基带离散信号

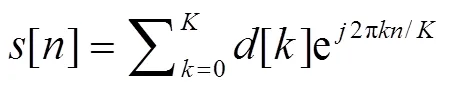
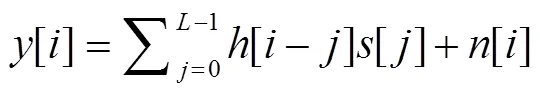
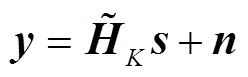
利用DFT可以对角化循环矩阵的性质, 对接收到的信号做DFT得

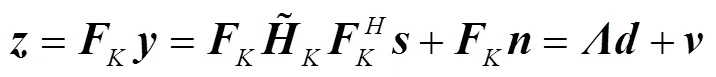
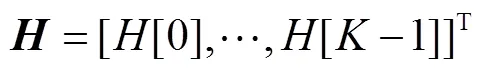
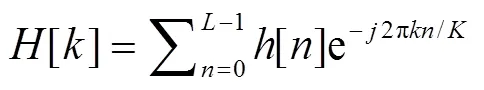
通过上述处理消除了码间干扰。假设接收端有完整的信道信息(channel state information, CSI),简单的均衡为

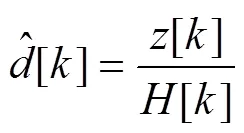
在现实通信中, 信道信息一般通过导频进行估计得到。下面对常见的梳状导频算法进行分析。

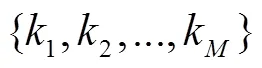
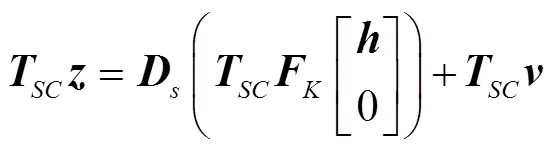
利用式(9)可以得到信道频域响应的估计值

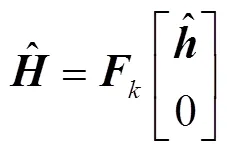
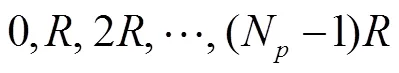
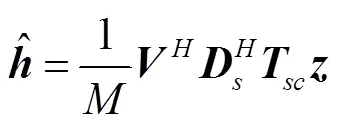
之后的分析中将要用到这种简化的算法。

2 同步误差对信道估计的影响

最基本的OFDM水声通信同步方式是用线性调频(linear frequency modulated, LFM)信号做相关, 寻找相关峰。LFM信号相关运算的优势是相关峰窄并且高。但劣势在于当遇到多途时, 会产生多个相关峰, 当信道条件不好时, 例如不存在直达路径的情况下, 第1个相关峰未必是最高峰。同步算法一般寻找最高峰进行同步, 但是OFDM均衡需要对第1个到达的相关峰进行同步, 如果寻找最大相关峰, 很可能错过第1个相关峰, 从而造成通过第1条路径到达的OFDM符号不完整, 并且引入下一个符号带来的码间干扰。

对于不同的导频算法而言, 同步误差也会对其造成不同的影响。

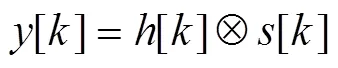
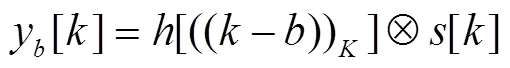
即同步偏移等价于信道的循环偏移。对其做DFT变换得

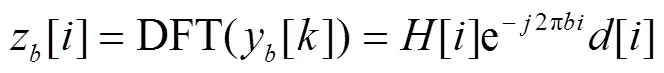
由式(13)可以看出, 同步误差在频域等价于信道频率响应加入了一个线性相位偏移。

由于每一块的同步误差均相同, 对于块状导频而言, 可以将式(15)中的相位偏移看作信道的一部分。利用导频进行估计时不加区分, 最终和信道频率响应一同进行均衡。

对于梳状导频而言, 情况就复杂很多。首先对信道冲击响应LS估计值进行简化, 方便分析。忽略式(9)中矩阵求逆项。文献[2]中的做法就利用了导频的等间隔排列使此项变为了单位矩阵, 得到式(11)。对式(11)中运算从左到右分析, 等价于通过下采样得到接收到的导频信号, 除以导频得到信道频率响应, 上采样插零恢复为点信号, 最后进行傅里叶变换, 保留前点结果。同步误差的影响主要是通过下采样接上采样产生的。

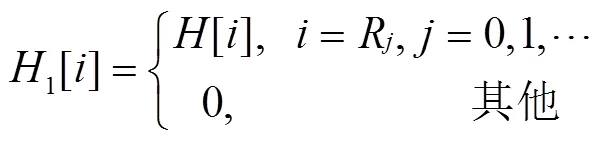
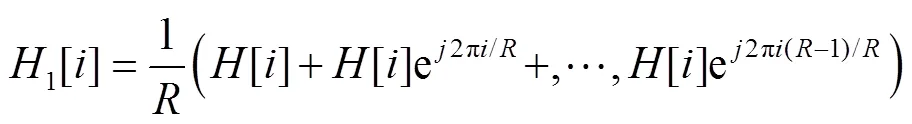
对应的时域信号为

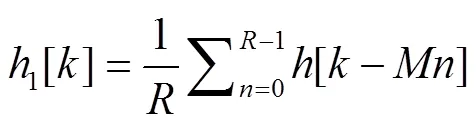
由式(16)可知, 经过频域下采样和上采样后,对应的时域信号是原始信号平移叠加的结果。当存在由同步误差引入的循环平移时, 截断后的估计结果会将末尾的抽头混叠到前端, 这将严重影响信道均衡效果。

3 对抗同步误差的稀疏信道估计

信道的稀疏性一直是各种信道估计算法的前提条件。在梳状导频信道估计中, 假设信道冲击响应抽头只存在于前个采样点中, 当出现同步误差时, 信道抽头会以为模循环平移, 导致上述假设不成立。假设同步误差为, 根据式(14), 平移后的等价信道为

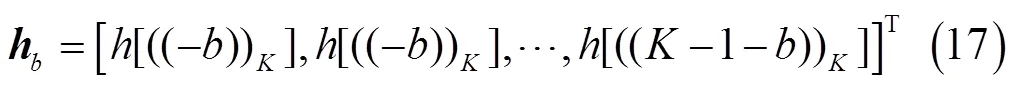
将其带入式(8)得到

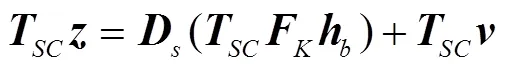
需注意的是尽管出现了循环平移, 但总的信道抽头数并没有改变, 仍然保持稀疏性质, 只是抽头位置无法预知。这实际上满足文献[5]中描述的通过不完整的频域信息重构大型稀疏信号问题。问题最终等价于要求建立一个凸优化模型[7]

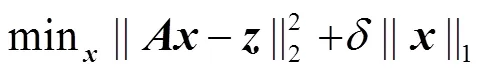
当是由DFT矩阵中随机抽取的某些行组成的, 并且行数大于中稀疏抽头的2倍时, 文献[5]中证明信号可以得到完整重构。将式(18)带入式(19)得

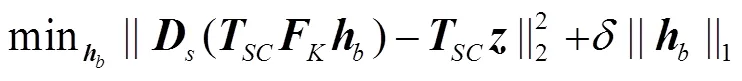
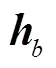
具体方法是在个子载波中平均的随机抽取个作为导频。的大小决定了信道估计的精度。导频与信息码元格式相同, 为随机生成的不相关的正交幅度调制(quadrature amplitude modulation, QAM)码元。对于收发两端, 上述均为已知信息。

式(20)不存在解析解, 但是有很多算法可迭代求近似解[8]。压缩感知算法最终得到的信道估计中会出现一些小的尖峰噪声, 使用文献[3]中的方法对估计信道进行自适应更新, 以平滑噪声,并保留真正的信道抽头。自适应更新由下式完成

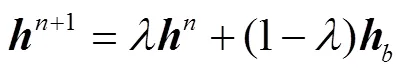
4 试验结果

该信道估计算法于2012年在湖上进行了试验验证。试验中水深约为50 m, 两船相距约为550 m。收发换能器均在水下5 m。

试验基本参数为采样频率48 kHz, FFT点数4 096点, 子载波间隔11.7 Hz, 带宽6 kHz, 调制方式4 QAM, 中心载波频率5 Hz, 有效子载波数427个。为了使用不同算法对相同数据进行分析,试验中未加入编码, 这样接收端可以将任意码元作为信号或者导频进行分析。

为了验证前文中的分析, 挑选某段信道环境比较恶劣的时间情况进行分析。如图1(a)所示,直达声幅度很小, 但是之后有3条能量很强的路径。一般会以能量最强路径的做同步, 如图1(b)所示, 图中信道出现了循环平移。对图1(b)中信道进行LS估计得图1(c)所示信道。可以看到, 图1(b)中末尾的路径抽头被搬移到了图1(c)中信道的前部。上述试验均与第2节中的理论分析相符。

压缩感知算法中, 分别在427个有效子载波中随机选择100个和140个子载波作为导频位置。在导频位置上插入与信号码元相同的不相关的4 QAM码元作为导频。图1(d)为利用压缩感知算法进行的信道估计, 图中几条路径都得到正确估计。为了平滑图1(d)中的尖峰噪声, 利用式(21)进行平滑, 结果如图1(e)所示。

图2中给出了多次试验中不同算法的比特误码率(bit error rate, BER) 对比图。图中将同步出现严重误差的帧排在前面, 后面是同步较精确的帧。由图可见, 由于同步误差, 前几帧使用LS均衡效果很差, 误码率高达20%~30%, 但是使用平滑后的压缩感知算法可以将其稳定在10%左右。当信号得到较精确的同步时, 平滑后的压缩感知算法误码率略高于LS算法, 这可以解释为压缩感知算法中需要估计的参数明显多于LS算法。但是在牺牲了较小的精确性的情况下, 压缩感知算法对同步误差提供了良好的健壮性。

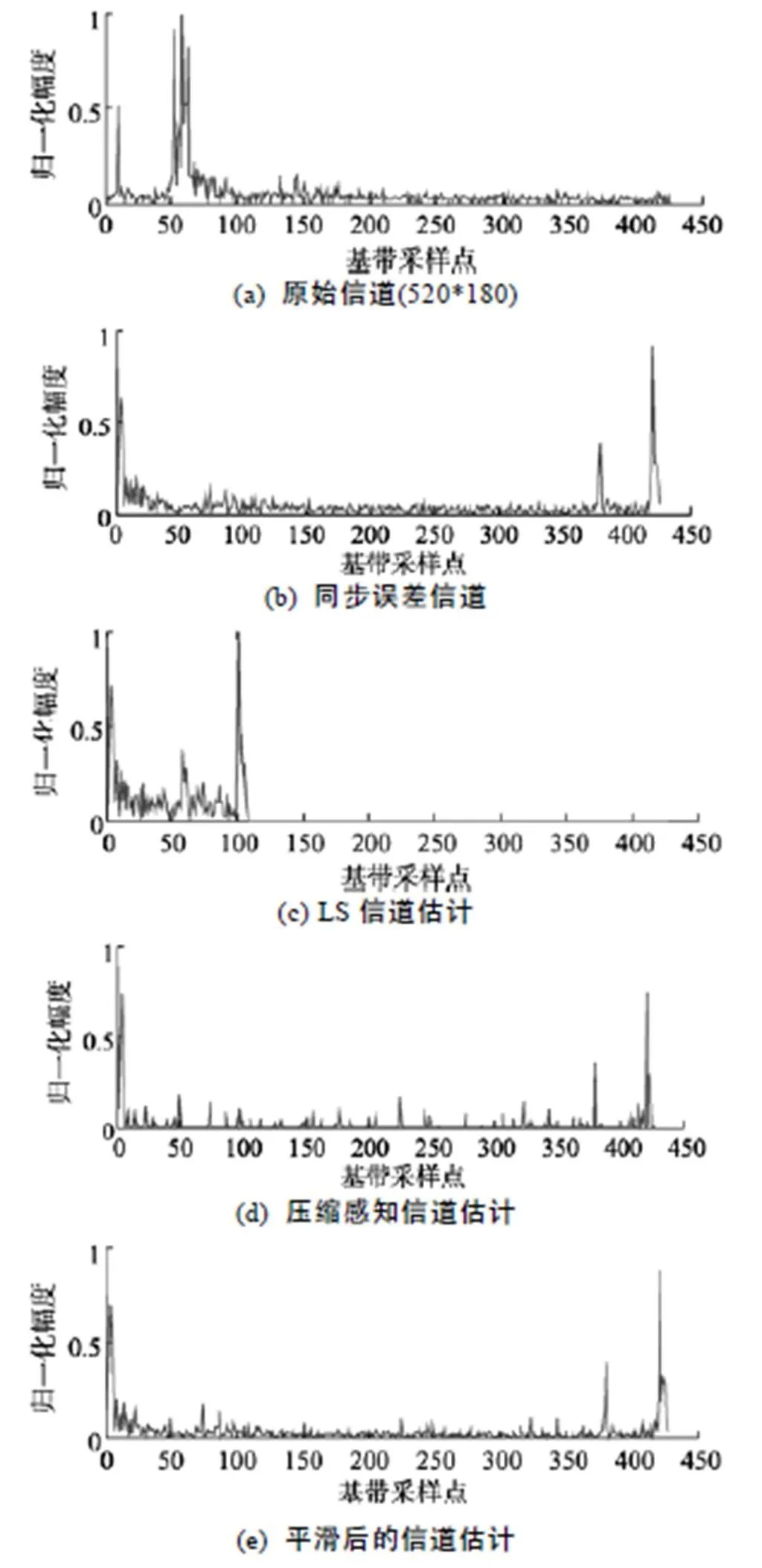
图1 信道估计

Fig 1 Channel estimation

5 结束语

本文对导频信道估计算法在实际水声信道中同步误差条件下的性能做出了分析, 提出了一种伪随机分布的导频分布方式, 从而建立了稀疏信号重构的模型, 通过压缩感知算法对信道做出了估计。经湖上试验验证, 可以完全避免由于同步误差造成的信道估计中的混叠问题。通过迭代更新降低了信道估计中的噪声, 提高了均衡性能。

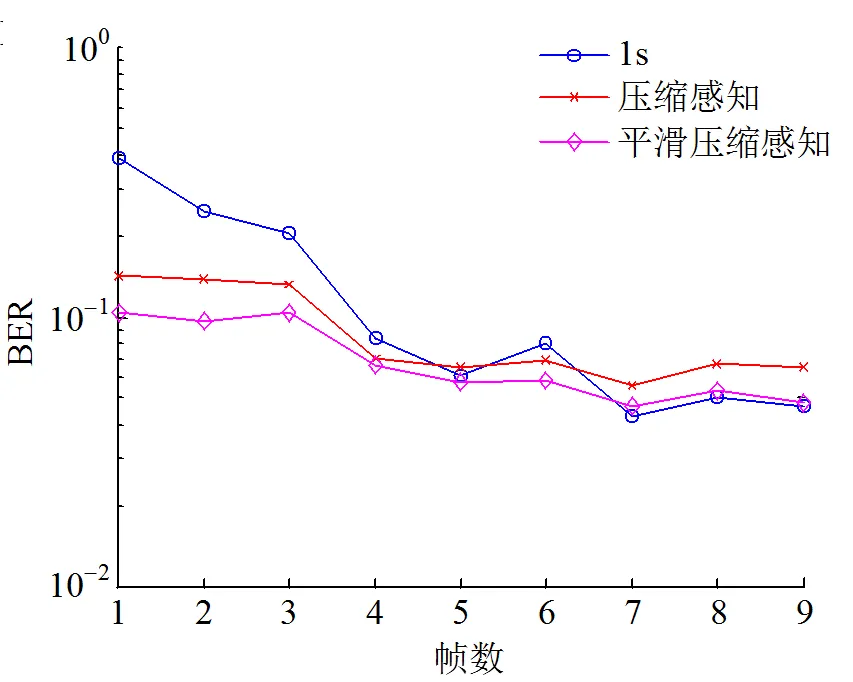
图2 比特误码率

Fig 2 Bit errors rate

[1] 朱彤. 基于正交频分复用的水声通信技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2004.

[2] Li B S, Zhou S, Stojanovic M. Pilot-tone Based ZP- OFDM Demodulation for an Underwater Acoustic Channel[C]//Oceans 2006, Boston, 2006.

[3] Stojanovic M. OFDM for Underwater Acoustic Communications: Adaptive Synchronization and Sparse Channel EstimAtion[C]//Process. ICASSP, Las Vegas, 2008: 5288- 5291.

[4] Berger C R, Zhou S, Preisig J C, et al. Sparse Channel Estimation for Multicarrier Underwater Acoustic Communication: From Subspace Methods to Compressed Sen- sing[J]. IEEE Transactions on Signal Processing, 2010, 58 (3): 1708-1721.

[5] Candes E, Romberg J, Tao T. Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Frequency Information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[6] Wang Z H, Zhou S, Giannakis G B, et al. Frequency- Domain Oversampling for Zero-Padded OFDM in Under- water Acoustic Communications[J]. IEEE Journal of Oceanic Engineering, 2012, 37(1): 14-24.

[7] Stephen Boyd, Vandenberghe l. Convex Optimization[M]. Cambridge University Press, 2004.

[8] Huang J Z, Berger C R, Zhou S, et al. Comparison of Basis Pursiut Algorithms for Sparse Channel Estimation in Un- derwater Acoustic OFDM[C]//Oceans 2010, Sydney, 2010.

[9] Stojanovic M. Low Complexity OFDM Detector for Underwater Acoustic Channels[C]//Oceans 2006, Boston, 2006.

Sparse Channel Estimation of OFDM with Synchronization Errors

WANG Xiao-zhou, ZHANG Yan, HU You-feng

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

An estimation algorithm of orthogonal frequency division multiplexing(OFDM) channel, which is robust with synchronization errors, is introduced. The severe synchronization error in general underwater channel might cause the aliasing in comb-pilot least square(LS) algorithm based channel estimation, if the strongest signal arrival is not the first one, therefore, a new OFDM sparse channel estimation algorithm is proposed by analyzing the influence of synchronization errors on the LS channel estimation algorithms. In the proposed estimation algorithm, sparse channel estimation with synchronization errors is equivalent to reconstructing a sparse signal from incomplete frequency samples. Some pseudo randomly picked subcarriers are used as pilots, and the compressed sensing(CS) algorithm is adopted for the sparse channel estimation. This algorithm can achieve better performance when synchronization error is large. Lake trial verifies the effectiveness of the proposed algorithm.

underwater acoustic communication; orthogonal frequency division multiplexing(OFDM); sparse channel estimation; synchronization error; compressed sensing

TJ630.34

A

1673-1948(2013)02-0095-05

2012-10-29;

2013-02-25.

船舶工业国防科技基金资助项目.

王小舟(1987-), 男, 在读硕士, 主要研究方向为水下通信技术.

(责任编辑: 杨力军)