基于遗传算法的鱼雷发射管优化设计

黄 科, 高 兴, 段 浩, 王 云



基于遗传算法的鱼雷发射管优化设计

黄 科, 高 兴, 段 浩, 王 云

(中国船舶重工集团公司第705研究所 昆明分部, 云南 昆明, 650118)

为了优化发射装置质量, 探讨大深度鱼雷发射管的优化设计方法, 通过解析法建立了鱼雷发射管在满足强度和稳定性要求的前提下, 质量达到最轻的优化设计数学模型, 并以MATLAB为平台采用遗传算法对该约束非线性混和离散变量优化问题进行全局寻优。计算结果表明, 在满足目前战技指标的前提下, 现有发射管在质量方面还有很大的优化余地, 但不能满足未来大深度发射时的要求。将管体的设计工作程序化, 具有一定的工程应用价值, 对鱼雷发射管管体优化设计具有一定参考意义。

鱼雷; 遗传算法; 发射管; 优化设计

0 引言

鱼雷发射管作为水中兵器发射装置的承压结构及发射通道, 均在水下工作和运行, 除了在发射时管内注有水外, 其他大部分时间管内为空气, 由此管外海水与管内空气形成压差, 在深潜时该压差可达几兆帕, 发射管管体不仅承受较大的外压作用, 还要承受发射过程巨大的压力脉动; 而随着潜艇下潜深度和鱼雷发射深度的增大, 必然要求鱼雷发射装置的最大潜射深度增加, 可引入新的发射原理以适应深度的变化, 同时发射管的结构在强度和稳定性方面都要满足更高要求。目前鱼雷发射管由前管、前中管、滑套阀和后管等多个部分组成, 其中前管和前中管占管体的绝大部分且处于耐压舱壁外, 长期浸泡在水中, 工作环境恶劣, 是管体的主要承压结构, 设计中需重点考虑它们的强度和稳定性, 滑套阀和后管则焊接在刚度较大的耐压舱壁围栏上, 结构得到加强, 且后管处于耐压舱壁内, 工作时仅受内压作用。本文将需承受外压作用的前管和前中管作为一个整体, 针对其优化设计工作进行研究。对于外压圆筒设计, 虽然靠增大壁厚、增多加强环个数以及增大加强环截面尺寸从而满足压力增大时的强度和稳定性要求, 但无法适应轻量化这一趋势。现代潜艇要求携带的装备越来越多, 而潜艇的承载能力有限, 潜艇一舱对发射装置的质量要求越来越严格, 所以在不影响作战效能的前提下, 降低装备质量显得尤为重要。

关于外压容器的设计, 相关标准(如GB150)介绍了图表法[1], 该方法的一个特点是需要查找相应材料的系数图, 若设计中需要采用某种特定材料但缺乏相关数据时, 就无法采用该方法, 并且需要反复多次的计算, 对于一般设计人员来说过于繁琐; 文献[2]介绍了解析法, 设计时需要先假设一组取值, 然后验证该组取值是否满足强度、刚度和稳定性要求, 否则需要调整所取数值, 重复验证计算, 直到满足要求为止, 所得结果也不一定能满足质量最优要求; 设计中还需注意管体壁厚、加强环个数及截面尺寸的取值都不是连续的, 需要满足规范和工艺的要求。优化设计的过程实际上是在这些离散的取值中选出一个最优组合, 所以鱼雷发射管轻量化设计是一个混合离散变量优化问题。

传统的优化方法先将离散变量当连续变量处理, 然后将所得“最优解”圆整[3], 这种方法不太适合工程应用, 所以需要采用离散变量优化方法, 如近些年发展起来的遗传算法和模拟退火算法等, 它们在船舶和建筑结构的优化设计方面已经有了很好的应用。

本文在考虑强度和稳定性的基础上, 建立了以管体质量最轻为目标的优化设计数学模型, 并以MATLAB为平台, 采用遗传算法求解该约束非线性混合离散变量优化问题, 实例计算结果表明, 该方法能快速得出满足要求的管体设计, 具有一定的工程应用价值。

1 结构强度及稳定性分析

如图1所示, 艇中发射管一端紧固在发射水舱壁, 另一端紧固在压载水舱壁, 这两处的管体可看作是刚性的, 管体失稳主要发生在两舱壁之间部分。当前盖关闭且内部未注水时, 管体受到海水压力的作用, 压力大小随潜艇下潜深度变化而变化。分析设计时, 必须根据潜艇的极限深度来确定计算压力。

图1 发射管水下受压示意图

1.1 管体强度

发射管管体采用高强度材料, 屈服极限达到500 MPa以上, 所以管体强度相对于其稳定性来说发生失效的可能性不大, 但为安全起见仍需对管体强度进行校核, 而且在采用Mises公式计算管体失稳临界压力时需要满足2个条件[2]:

对于圆筒, 条件2)能够满足, 所以在采用Mises公式计算时只需保证条件1), 而1)又与第1和第3强度理论的要求相符合。因此, 对于焊接圆筒, 在考虑焊缝对强度的影响后, 由条件1)可推出筒体的最小厚度为

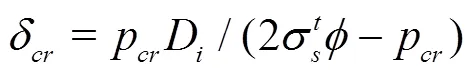
此外, 在靠近前中管后凸缘处, 因释放上制止器, 鱼雷档块需要开有两个矩形小孔, 如图2所示。开孔会对管体的强度产生一定的影响, 但其上焊接的上制止器箱将开孔封闭在内, 还对该处进行了局部加强, 所以文中不考虑开孔对管体强度的影响。

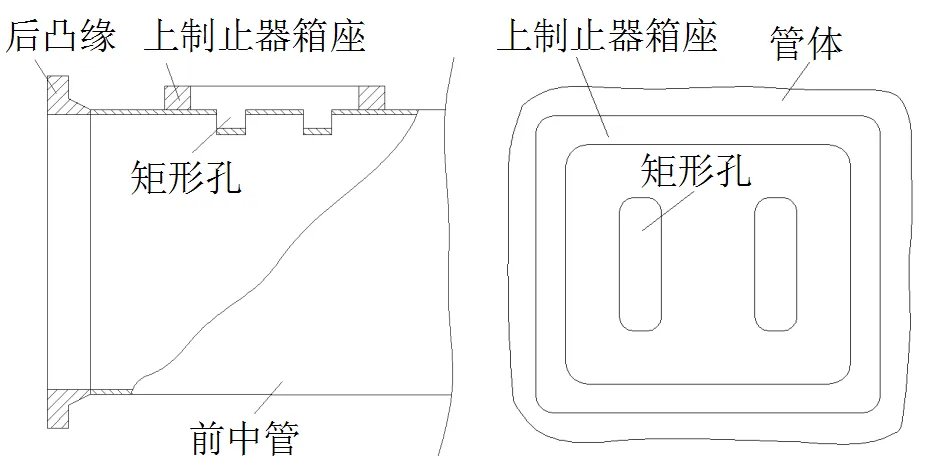
图2 管体开孔示意图

1.2 失稳临界压力分析

外压圆筒失稳临界压力的计算公式因筒体计算长度不同而有长圆筒和短圆筒的差别, 两者间的临界长度为

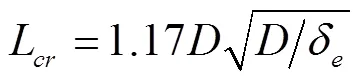
外压薄壁短圆筒在四周受压力作用时, 其临界压力为

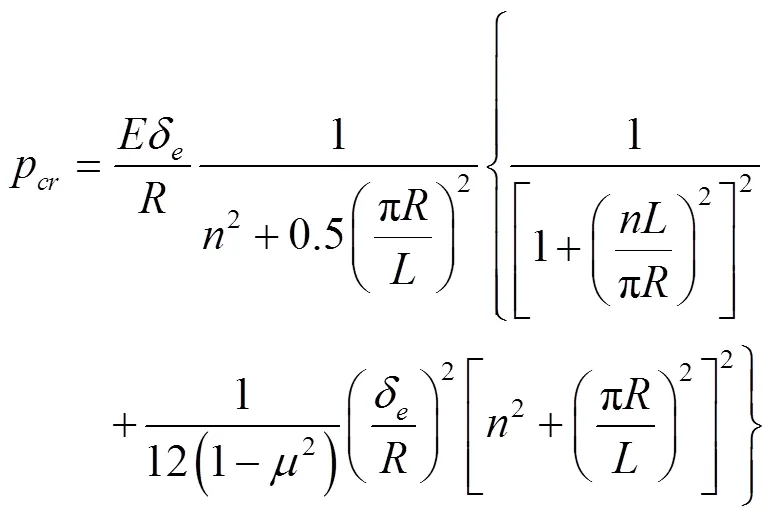
麦克公式

表1 波形数圆整值

1.3 加强环刚度分析

加强环刚度与截面形状和尺寸有关, 由于水中兵器所接触的介质(海水)有很大的腐蚀性, 所以发射管上的加强环不宜采用腹板厚度较小的型钢, 如工字钢、槽钢等; 此外, 对相同厚度相同截面尺寸的加强环, 扁钢比T型钢组合惯性矩更大[4], 故设计时加强环采用具有矩形截面的扁钢。

图3 加强环与筒体截面

2 数学模型的建立

2.1 设计变量

2.2 目标函数

以质量最优为目标, 目标函数为如下形式

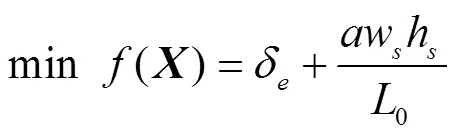
该式的物理意义即为筒体的当量厚度, 其值越小则耗材越少, 筒体质量也越轻。

2.3 约束条件

由结构分析部分可知, 优化设计需要满足强度和稳定性等性态约束条件; 此外, 根据制作工艺和板材选择等方面的限制, 还需要满足一些辅助约束条件。

强度条件

短圆筒条件

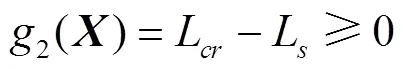
稳定性条件

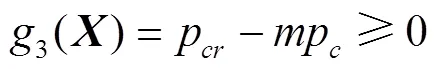
最小惯性矩条件

辅助约束条件: 规范规定对于不锈钢制品,容器壁厚需大于2 mm; 板材厚度也应符合冶金产品标准, 热轧钢板厚度尺寸为4~6 mm, 每档间隔0.5 mm; 6~30 mm, 间隔1.0 mm, 30~60 mm, 间隔2.0 mm; 加强环个数不能过多, 否则间距过小不便于布置施工; 加强环截面尺寸也应在扁钢的规定范围内。

3 优化方法

3.1 算法选择

该数学模型为约束非线性混合离散变量的优化问题, 文献[3]在处理相关问题时, 先将离散变量当作连续变量, 然后采用传统的优化方法来处理该有约束的优化问题, 再将得到的最优解圆整到规定的离散值上, 该方法虽然能较快的收敛, 但按连续变量优化得到的“最优解”圆整到相邻的离散值时, 会产生多种组合, 这些组合中有的可能已经不在可行域内, 有的即使在可行域内也仅为局部最优解, 因此, 本文采用了能直接处理离散变量的遗传算法。

3.2 算法实现

遗传算法的基本思想是根据问题的目标函数构造一个适值函数, 对一个由多个解(每个解对应一个染色体)构成的种群进行评估、遗传运算、选择, 经多代繁殖, 获得适应值最好的个体作为问题的最优解[5]。

式中,(k)为惩罚因子, 是一个大于零的递增数列。

在惩罚项中

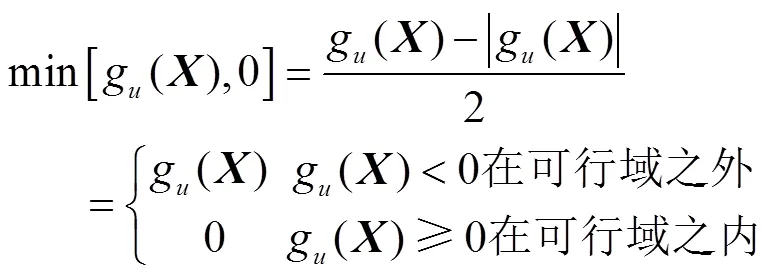
此方法的优点是能提前计算好选择概率, 节省算法执行时间, 并且选择压力可控。得到选择概率后, 采用旋轮法来实现选择操作。

此外遗传算法实现过程中还要考虑的因素有种群大小, 遗传代数, 交叉率及变异率, 其数值的选取会对收敛速度和结果产生影响。作者根据前面所述方法运用MATLAB软件编写了相应的计算程序, 可根据设计要求改变程序中计算压力, 管体长度和内径以及材料的屈服极限以进行优化设计分析。

3.3 实例分析

设某发射管管体总长4 000 mm, 内径570 mm, 计算压力3.5 MPa, 稳定系数取3, 管体壁厚按2.3节中所述取[4, 30]间的值, 加强环个数取[1, 15]间的整数。根据扁钢规格表, 加强环厚度按[10:12 14:2:22 25 28 30]选取, 高度按[12:2:22 25 28 30 32 35 36]选取, 以上长度单位均为mm。

表2 不同计算压力下的优化结果

以上结果表明, 目前的管体设计对现阶段的发射要求来说是安全的, 而且有较大的优化余地。在此, 继续增大计算压力, 考察大深度发射情况下的管体设计, 优化结果如表3所示。

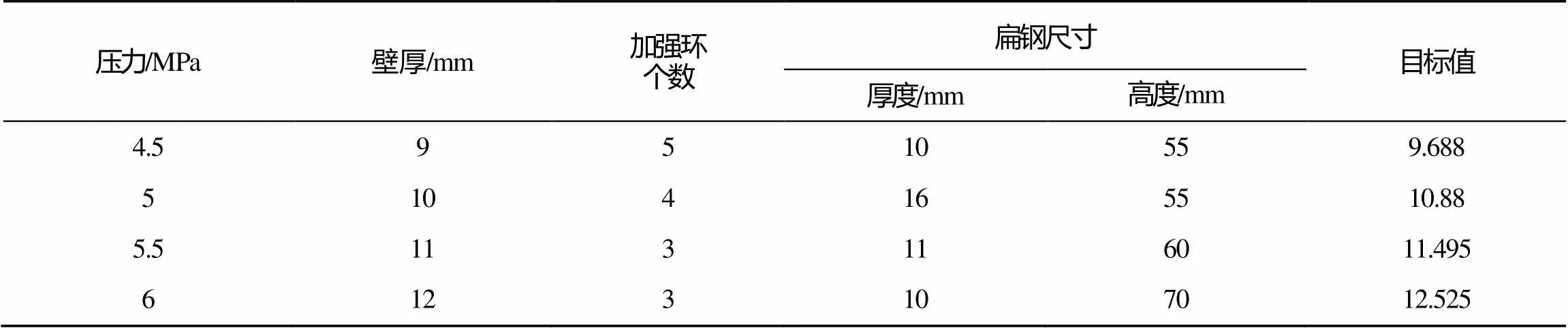
表3 大深度条件下的优化结果

优化迭代计算结果表明, 在大深度发射时, 现有发射管的管体设计已不能满足要求, 尤其是加强环的尺寸, 目前设计中采用的加强环刚度过小, 不能保证管体在大深度时不失稳, 因此在大深度发射装置的管体的设计中, 需要采用截面尺寸更大的加强环。

从优化过程可以发现, 遗传过程会优先选择壁厚小而加强环个数多的组合, 这与这两个因素对管体稳定性的影响有关, 因为在管体保持稳定的前提下, 减小加强环间距可以减小壁厚; 此外, 加强环厚度小而高度大的组合会优先保留下来, 这是因为在截面积相同的情况下, 高度越高其截面惯性矩越大, 因此在人工设计时可以利用上述规律, 结合尺寸的约束条件, 对管体进行合理设计, 使得相对情况下管体更轻。

4 结束语

本文将遗传算法引入到鱼雷发射管的优化设计中, 设计时只需按设计要求改变现有程序中的相关参数, 就能快速获得最优设计结果, 从而使得发射管的管体设计变得方便易行。实例计算结果表明, 在满足同样环境压力要求的情况下, 采用该方法设计的管体较现有管体轻了17.8%, 并且能够满足发射装置几何尺寸的约束条件。文中还提出了大深度发射时发射管强度和稳定性的优化设计方法。

[1] 全国压力容器标准化技术委员会. GB150-1998 钢制压力容器[S]. 北京: 中国标准出版社, 1998.

[2] 化工设备设计全书编辑委员会. 化工容器设计[M]. 上海: 上海科学技术出版社, 1987.

[3] 梁基照. 压力容器优化设计[M]. 北京: 机械工业出版社, 2010.

[4] 闫雪莲. 浅谈外压圆筒及其加强圈的设计[J]. 应用能源技术, 2010(5): 13-15.Yan Xue-lian. Design of Stiffeners for External Pressure Vessel Shell[J].Applied Energy Technology, 2010 (5): 13-15.

[5] 汪定伟, 王俊伟. 智能优化方法[M]. 北京: 高等教育出版社, 2007.

Optimization Design of Torpedo Launch Tube Based on Genetic Algorithm

HUANG Ke, GAO Xing, DUAN Hao, WANG Yun

(Kunming Branch of the 705 Research Institute, China Shipbuilding Industry Corporation, Kunming 650118, China)

To optimize the weight of torpedo launch tube and perform optimization design of large depth torpedo launch tube, a mathematical model is built with analytical method, and genetic algorithm is adopted to acquire the global optimal solution of the nonlinear discrete optimization problem for the minimum weight design of torpedo launch tube meeting strength and stability requirements on MATLAB platform. Results indicate that on the premise of meeting the existing tactical and technical indexes, there is still a large space for the weight optimization design of existing launch tube, but the existing launch cannot meet the requirement of large depth launch in the future. This study programs the design of torpedo launch tube for the purposes of engineering application and benefiting optimization design.

torpedo; genetic algorithm; launch tube; optimization design

TJ635

A

1673-1948(2013)02-0156-05

2012-11-12;

2012-12-03.

黄 科(1987-), 男, 在读硕士, 主要研究方向为水下发射技术.

(责任编辑: 许 妍)