故障状态下电网电压自愈策略研究
卢锦玲,白丽丽,杨仁刚
(1.中国农业大学信息与电气工程学院,北京 100083;2.华北电力大学电力系,河北 保定 071003)
0 引言
当电网发生严重故障时,快速、有效地使系统从故障状态转移到优化的稳定运行状态,是电网自愈功能的主要任务之一[1-5]。尤其是当前电力系统广域互联的逐步实现及电力市场的深入发展,电压稳定问题日益突出[6],一旦发生电压失稳事故,将会带来波及范围广、经济损失严重等一系列问题。因此,研究能够适应系统变化,在异常情况下能够自我恢复,可有效防止电压失稳事件的电压自愈策略,有着重要的现实意义[7-8]。
电力系统电压稳定程度一般可分为三种情况[9]:系统平衡点不存在,电压处在崩溃/失稳过程中;系统接近不稳定边界,电压稳定裕度紧张;系统能够满足各种约束条件,电压稳定裕度较大。相应地电网的运行状态可分为故障状态、脆弱状态、正常状态。根据系统运行状态的不同,同时参照文献[3]对电网自愈控制的划分,本文将电压自愈控制分为故障状态下电压自愈控制、脆弱状态下电压自愈控制和正常状态下电压自愈控制,下面将重点研究故障状态下的电压自愈控制。
故障状态下电压自愈控制,是指当系统发生严重故障后电压处在崩溃/失稳过程中,为了防止事故的进一步扩大而采取的紧急措施,其实质是如何防止电压失稳。近年来,电网稳定问题一直是电力界关注和研究的热点之一,在电压失稳机理、电压稳定模型及电压稳定性评价等方面均取得了重要成果,但是在故障后如何采取有效的、经济的、协调的紧急控制措施,以防止系统发生电压崩溃,保证电网安全稳定运行,尚需进一步的研究[6]。当电压处在崩溃/失稳过程中,快速切负荷成为有效控制手段,如:文献[10]基于连续潮流,提出了预防支路型失稳故障的控制方法;文献[11]利用降出力法求出系统最薄弱输电通道,然后根据电压相角对有功注入灵敏度确定切负荷方案;文献[12]利用线路导纳递减算法求出发生失稳故障时系统无法承受的有功功率,然后采用双向潮流追踪法,得到发电/负荷减载量,但只考虑了线路有功潮流的影响,在故障线路潮流以无功功率为主的情况下,可能造成控制方案失效。尽管上述文献对系统失稳时的各种减载方法已经提出,但是这些方法都针对防止电压失去稳定问题而言,并没有考虑到恢复电压稳定后,要维持系统较高电压水平应采取的控制措施。
由于电力系统的高度复杂性和非线性,合理的电压控制方案在保证电压稳定的同时应维持系统较好电压水平[9]。本文根据系统电压稳定性和电压幅值,将电压自愈分为恢复电压稳定和提高节点电压两阶段。在前一阶段中,采用负荷裕度指标判断系统是否发生电压失稳,若失稳,则根据故障前潮流基于图论法确定故障转移负荷,并采用二分法逐次切除,直至电压恢复稳定;在后一阶段中,判断是否存在电压低于低压减载装置动作值的节点,若存在,则根据故障后潮流基于图论法得到经过这些节点的供电路径及其传输功率,并采用二分法逐次切除负荷,直至所有节点电压达到预定值。
1 图论法
目前,电压控制的研究模型和分析方法多种多样,并取得了很大的进展,但仍存在一些问题尚需解决,其中,如何减少系统非线性、复杂性对控制策略的影响就是电压控制方面应进一步研究的课题[13]。因此,本文采用物理意义明确、计算速度快、受系统非线性和复杂性影响较小的图论法对故障状态下电压自愈策略进行研究。
1.1 无损网等效
图论法要求注入节点量与流出节点量相等,而电力系统是一个有损网,因此,首先要将原网络等效为无损网,计算公式如式(1)所示。
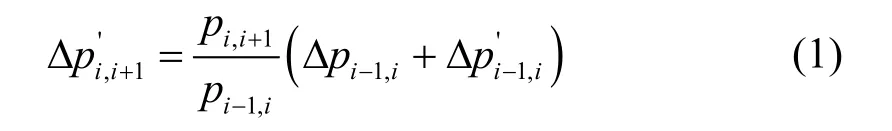
1.2 供电路径确定
所谓供电路径就是发电机节点与负荷节点间的输电通道,它反映了系统中各个电源是怎样通过输电网络的哪几条线路将电能输送到用户的,是后续确定切负荷位置的基本依据。本文用到图论法的有向图关联矩阵和有向图路径矩阵来确定电力系统的供电路径。
有向图关联矩阵表示有向图中两节点间是否存在有向边,假设系统中有n个节点,则关联矩阵A为n×n的方阵,其元素可表示为

有向图路径矩阵表示有向图中两节点间是否存在有向路径,假设系统中有n个节点,则路径矩阵L为n×n的方阵,其元素可表示为

假设系统潮流已知,利用关联矩阵和路径矩阵,采用深度优先搜索算法,即可得到该系统所有发电机节点与负荷节点间的供电路径。
1.3 供电路径传输功率计算
采取切负荷措施除了要知道切负荷位置外,还要知道切负荷量,即供电路径的传输功率。本文采用“按比例分配”原则计算供电路径传输功率。所谓“按比例分配”原则是指“不同支路流入节点功率对流出节点的每条支路上功率的贡献是与其流入节点的功率值成正比[14]”。假设第l条供电路径有m个节点,其中第一个节点为发电机节点,最后一个节点为负荷节点,则该供电路径的传输功率lp为
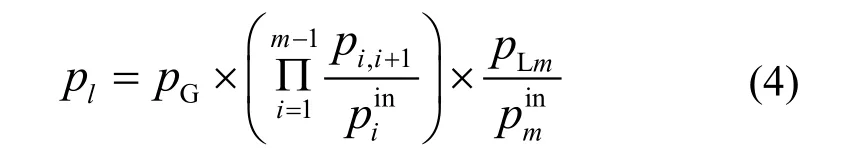
式中:pG表示发电机节点注入功率;pi,i+1表示节点i与节点 i+1间支路功率;表示注入节点i的总功率;pLm表示负荷节点输出功率;表示注入负荷节点的总功率。
2 故障状态下电压自愈策略
衡量一种电压控制方案是否合理可行,既要看其是否能够保证系统电压稳定,同时又要看能否维持系统电压水平。为了实现该目标,本文将故障状态下电压自愈分为恢复电压稳定和提高节点电压两阶段,前者用来保证电压稳定性,后者用来维持节点电压。
2.1 恢复电压稳定
当电力系统发生严重故障,系统失去稳定平衡点是由于故障线路所带负荷发生转移,导致某些薄弱输电通道超过其极限输送能力造成的[11-12],因此,若知道故障前该线路为哪些负荷节点供电及供应了多少电能,即故障转移负荷的位置及数量,在故障后对其采取切负荷措施即可快速恢复电压稳定。
本文根据故障前系统潮流,基于图论法确定故障转移负荷,然后采用二分法计算能够恢复电压稳定的最佳切负荷方案,其具体步骤如下。
(1) 根据故障前潮流,基于图论法得到所有包含故障支路的供电路径,并计算其传输功率。这些路径的末端节点即为故障转移负荷所在的负荷节点,首端节点即为相应的发电机节点,路径上的传输功率即为各节点的转移负荷分担量。
(2) 对包含故障支路的供电路径按传输功率由大到小进行排序,切除第一个供电路径末端负荷节点的有功功率和无功功率,同时相应地减少首端发电机节点的有功出力。图论法中只对负荷节点的有功功率进行了计算,其无功功率可由式(5)得出。
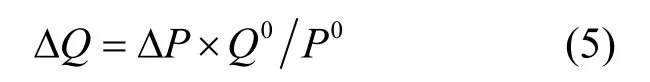
式中:P0、Q0表示负荷节点的初始有功功率和无功功率;PΔ、QΔ表示负荷节点切除的有功功率和无功功率。
(3) 判断系统是否恢复稳定,若恢复稳定,则采用二分法减少切负荷量直至满足终止判据,否则转向步骤(2)。二分法的计算步骤如下:
③若电压恢复稳定,则b=c,否则a=c;
④判断是否达到计算精度ξ,若b − a <ξ,则最终切负荷量确定为b,退出恢复电压稳定子程序;否则,转向步骤②。
2.2 提高节点电压
在实际电力系统中,为了防止因电压严重下降引起电压崩溃广泛采用了低压减载装置。低压减载装置的动作值一般是按略高于PV曲线鼻点电压而低于正常运行时的最低电压整定的。
当系统发生严重故障,按2.1 节所述方法恢复电压稳定后,很可能存在一些电压低于低压减载装置动作值的节点。由于这些节点运行在电压崩溃点附近,极易发生失稳,严重地威胁了系统安全,因此有必要将提高这些节点电压加入到故障状态下电压自愈控制中,其具体步骤如下:
(1) 根据故障后潮流,基于图论法计算所有发电机节点与负荷节点间的供电路径及传输功率。
(2) 找到所有电压小于低压减载装置整定值的节点,并从中选出电压最低节点。搜索经过最低电压节点的所有供电路径,并按传输功率由大到小进行排序,切除第一个供电路径末端负荷节点的有功功率和无功功率,同时相应地减少首端发电机节点的有功出力。判断该节点电压是否大于低压减载装置动作值,若大于,则采用二分法减少切负荷量,直至满足终止判据。
多样性指数变化体现了3类生态系统间组织结构变化(图2),草地、人工林和次生林系统灌草层的Margalef丰富度指数(R)分别是4.11、2.22、4.88,且系统间有显著差异(F=5.63,P=0.005)。3类生态系统间的Shannon-Wiener指数、Simpson指数和Pielous均匀度指数差异不显著。草地Margalef丰富度指数、Shannon-Wiener指数和Simpson指数高于人工林,人工林物种的Pielous均匀度指数高于草地。综合来看,次生林系统的灌草层物种多样性指数高于人工林和草地。
(3) 判断是否存在电压小于低压减载装置整定值的节点,若存在,则返回步骤(2),反之,则退出。
以上方法虽然每次只对电压最低节点采取控制措施,但由于各节点是相互联系、相互影响的,且电压薄弱点在地理分布上通常集中于某个区域,因此在恢复最低点电压时,也可有效地提高相邻节点电压。通过IEEE30节点系统和某地区17节点系统算例分析可知,该算法的循环次数均小于低电压节点数。
2.3 故障状态下电压自愈控制流程图
故障状态下电压自愈控制流程如图1所示,基本步骤如下:
(1) 通过状态估计或在线潮流实时记录系统当前运行状态;
(2) 当系统发生故障,维持系统稳定是首要任务,因此首先判断系统是否失稳,若系统失稳,则执行恢复电压稳定子程序;
(3) 若系统没有失稳或者恢复电压子程序执行完毕,则判断是否存在电压小于低压减载装置整定值的节点,若存在,则执行提高节点电压子程序,反之,则退出该程序。
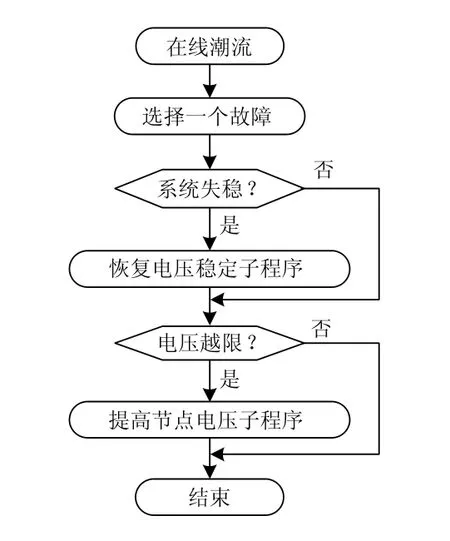
图1 故障状态下电压自愈控制流程图Fig.1 Flow chart of voltage self-healing control under fault condition
3 算例分析
应用上述理论,编制电压自愈控制程序,分别对IEEE30节点系统和某地区17节点系统进行仿真计算,以验证本文所提方法的有效性。
3.1 IEEE-30节点系统算例
由于该网络结构紧密,基荷情况下不存在使电压失稳的线路故障,因此首先令负荷和发电机出力按比例同时增长,使系统运行至793.46 MW 负荷水平。本文选取了5个典型故障进行仿真计算,其中:故障1、4、5可使电压失稳,故障2、3 虽不会使电压失稳但故障后存在电压小于低压减载装置动作值的节点。算例中,低压减载装置动作值取0.8[15]。
表1给出了发生上述5个故障时各子程序运行情况。由表中数据可以看出,当发生失稳故障1、4、5时,该自愈策略首先运行恢复电压稳定子程序,通过切负荷使电压快速恢复稳定,然后再考虑提高节点电压。而当发生故障2、3时,由于系统没有失稳,因此该自愈策略直接运行提高节点电压子程序。
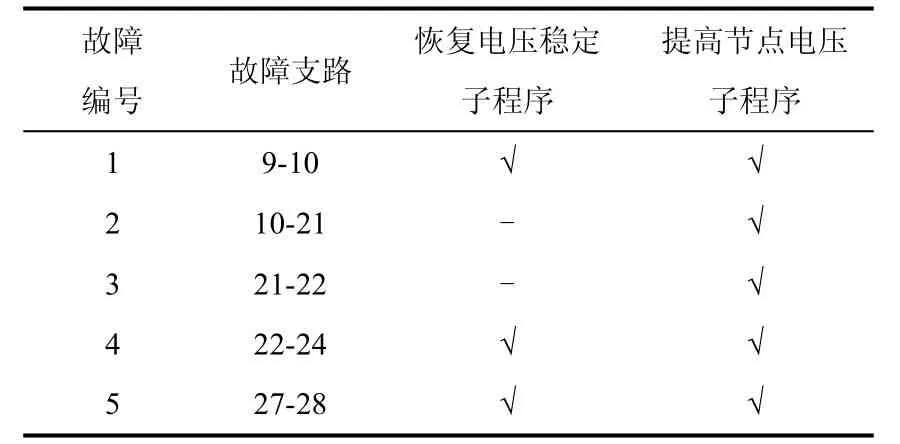
表1 故障状态下电压自愈控制各子程序运行情况Table1 Running condition of voltage self-healing control subroutines under fault condition
表2给出了各故障的自愈控制结果。其中,负荷裕度是按全系统负荷和发电机出力同比增长确定的,切负荷量是恢复电压稳定和提高节点电压两部分的切负荷总和,控制效果σ 按式(6)计算。
表3给出了针对故障5的具体自愈控制方案,该方案中发电裁减量与负荷裁减量相等,线路损耗由平衡机承担。
结合表2、表3的数据,以故障5为例,对该电压自愈控制进行详细分析:系统发生故障5后,负荷裕度降为-380.889 6 MW,系统失稳,若按等比例方法恢复电压稳定,则要切除380.889 6 MW的负荷。而由本文所提方法分析可知,支路27-28 故障后系统失稳是由于其所带负荷发生转移导致某些薄弱输电通道严重越限造成的,因此对转移负荷采取切负荷措施即可快速恢复稳定。运行该自愈控制程序后发现仅需切除29.858 7 MW的负荷即可使电压恢复稳定,继续切除15.125 5 MW的负荷即可使所有节点电压达到低压减载装置整定值,同时具有254.502 2 MW的负荷裕度,相当于用29.8587+15.1255=44.9842 MW的代价换来了 254.5022+380.8896=635.3918 MW的负荷裕度,其等效控制效果为635.3918/44.9842=14.12。同样,对其他故障均有类似结果。
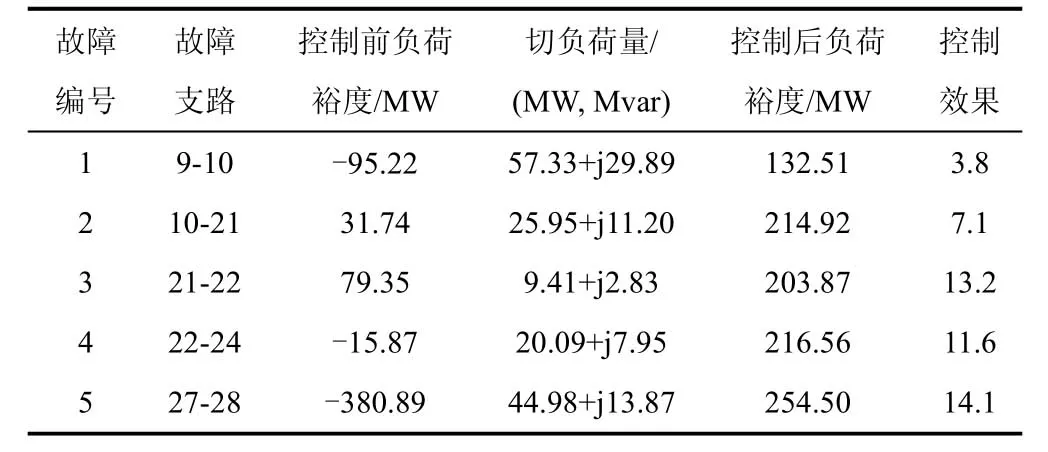
表2 IEEE30节点系统故障状态下电压自愈控制结果Table2 Result of voltage self-healing control under fault condition for IEEE 30-bus system
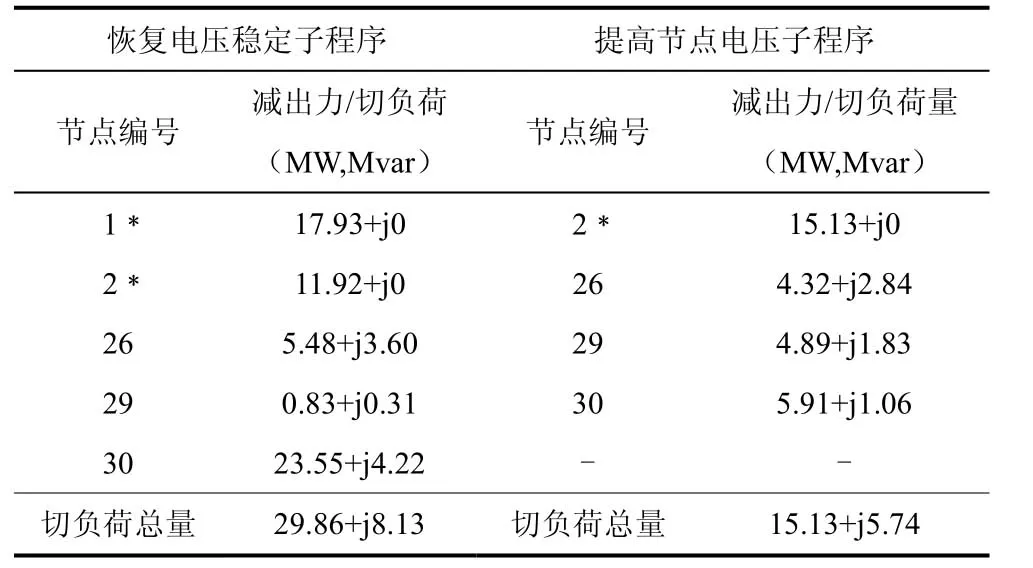
表3 IEEE30节点系统故障状态故障5 自愈控制方案Table3 Self-healing control strategy of the fifth fault under fault condition for IEEE 30-bus system
为了进一步验证文中所提方法的有效性,图2给出了运行该自愈控制程序后节点电压曲线。从图中可以看出,系统所有节点电压均在0.8以上,达到了系统运行要求。
3.2 某地区17节点系统算例
当该实际系统运行在30.25 MW的负荷水平时,通过故障扫描后发现存在使电压失稳的故障,本文选取了4个失稳故障进行仿真计算。
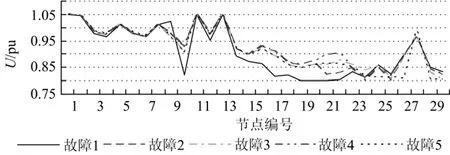
图2 IEEE30节点系统故障状态下自愈控制电压曲线Fig.2 Voltage curve of self-healing control under fault condition for IEEE 30-bus system
表4给出了各故障的自愈控制结果,图3给出了自愈控制后系统节点电压曲线。由这些计算结果可以得出,本文所提方法能够以较少的切负荷量保证电压稳定,同时使所有节点电压达到低压减载整定值以上。但与IEEE30节点系统仿真计算结果相比,该实际算例的控制效果明显较低,主要原因是该实际系统网架结构薄弱,各节点联系不如IEEE30节点系统中各节点联系紧密,单个节点切除负荷对周围节点电压影响较小。
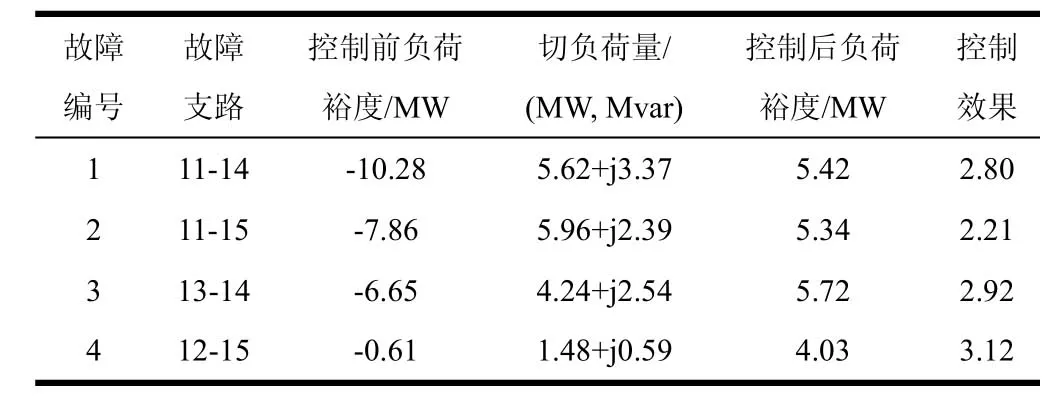
表4 某地区17节点系统故障状态下电压自愈控制结果Table4 Result of voltage self-healing control under fault condition for a regional 17-bus system
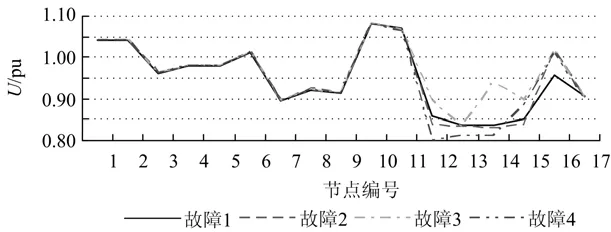
图3 某地区17节点系统故障状态下自愈控制电压曲线Fig.3 Voltage curve of self-healing control under fault condition for a regional 17-bus system
4 结论
针对电力系统发生严重故障的情况,本文提出了一种故障状态下的电压自愈策略,IEEE30节点系统和某地区17节点系统的仿真计算结果验证了该方法的有效性。
(1) 该方法将故障状态下的电压自愈控制分为恢复电压稳定和提高节点电压两阶段,在保证电压稳定的前提下,能够使节点电压维持在一定水平;
(2) 在恢复电压稳定子问题中,基于图论法确定故障转移负荷,并采用二分法切负荷,以较小的切负荷量保证了系统的稳定;在提高节点电压子问题中,将低压减载装置动作值作为控制目标,既维持了节点电压水平,也可有效地防止过多切负荷。
(3) 由于图论法仅与系统结构有关,与负载程度无关,因此该方法可以有效地避免在重负荷情况下较大的线性误差对计算精度的影响;同时在实际电力系统中发电机节点与负荷节点的供电路径数量有限,因此受系统规模和复杂程度的影响较小。
(4) 如何使切负荷节点数目最小化是工程实用化的关键之一,文中按传输功率由大到小排序进行切负荷的方法,既实现了快速切负荷,也有效地减少了切负荷节点个数,有利于工程实现。
对发生严重故障的系统采取上述自愈控制后,其电压稳定裕度可能较小或者系统电压对各用电设备来说并不是最优的,在这种情况下就需要继续对系统运行状态和结构进行调整,以进一步提高电压稳定裕度、优化系统电压,这些将是后续脆弱状态下电压自愈策略有待解决的问题。
[1]李兴源,魏巍,王渝红,等.坚强智能电网发展技术的研究[J].电力系统保护与控制,2009,37(17):1-7.
LI Xing-yuan,WEI Wei,WANG Yu-hong,et al.Study on the development and technology of strong smart grid[J].Power System Protection and Control,2009,37(17):1-7.
[2]何光宇,孙云生,梅生伟,等.多指标自趋优的智能电网[J].电力系统自动化,2009,33(17):1-5.
HE Guang-yu,SUN Yun-sheng,MEI Sheng-wei,et al.Multi-indices self-approximate-optimal smart grid[J].Automation of Electric Power Systems,2009,33(17):1-5.
[3]郭志忠.电网自愈控制方案[J].电力系统自动化,2005,29(10):85-91.
GUO Zhi-zhong.Scheme of self-healing control frame of power grid[J].Automation of Electric Power Systems,2005,29(10):85-91.
[4]陈铁军,宁美凤.基于分布式MAS的电网自愈控制方案研究[J].电力系统保护与控制,2012,40(19):14-18.
CHEN Tie-jun,NING Mei-feng.Study on self-healing control scheme of power grid based on distributed MAS[J].Power System Protection and Control,2012,40(19):14-18.
[5]李天友,徐丙垠.智能配电网自愈功能与评价指标[J].电力系统保护与控制,2012,40(19):14-18.
LI Tian-you,XU Bing-yin.Self-healing and its benchmarking of smart distribution grid[J].Power System Protection and Control,2012,40(19):14-18.
[6]张芳,房大中,陈家荣,等.最优协调电压紧急控制新模型研究[J].中国电机工程学报,2007,27(10):35-41.
ZHANG Fang,FANG Da-zhong,CHEN Jia-rong,et al.Study on novel for optimal coordinated voltage emergency control[J].Proceedings of the CSEE,2007,27(10):35-41.
[7]王明俊.自愈电网与分布能源[J].电网技术,2007,31(6):1-7.
WANG Ming-jun.Self-healing grid and distributed energy resource[J].Power System Technology,2007,31(6):1-7.
[8]林宇锋,钟金,吴复立.智能电网技术体系探讨[J].电网技术,2009,33(12):8-14.
LIN Yu-feng,ZHONG Jin,WU Fu-li.Discussion on smart grid supporting technologies[J].Power System Technology,2009,33(12):8-14.
[9]周双喜,朱凌志,郭锡玖,等.电力系统电压稳定性及其控制[M].北京:中国电力出版社,2004.
[10]赵晋泉,江晓东,张伯明.一种用于预防支路型失稳故障的灵敏度方法[J].中国电机工程学报,2004,24(12):69-73.
ZHAO Jin-quan,Chiang Hsiao-dong,ZHANG Bo-ming.A sensitivity method for prevention of branch type insecure contingency[J].Proceedings of the CSEE,2004,24(12):69-73.
[11]李敏,陈金富,陈海焱,等.一类潮流计算无解的实用性调整研究[J].电力系统自动化,2006,30(8):11-15.
LI Min,CHEN Jin-fu,CHEN Hai-yan,et al.Load flow regulation for unsolvable cases in a power system[J].Automation of Electric Power Systems,2006,30(8):11-15.
[12]魏炜,张忠华,贾宏杰,等.一种利用潮流追踪的电压稳定紧急控制方法[J].中国电机工程学报,2008,28(1):1-5.
WEI Wei,ZHANG Zhong-hua,JIA Hong-jie,et al.A voltage stability control method based on power flow tracing[J].Proceedings of the CSEE,2008,28(1):1-5.
[13]傅旭,王锡凡,杜正春.电力系统电压稳定性研究现状及其展望[J].电力自动化设备,2005,25(2):1-9.
FU Xu,WANG Xi-fan,DU Zheng-chun.Survey of power system voltage stability study[J].Electric Power Automation Equipment,2005,25(2):1-9.
[14]武志刚,张尧,宋文南,等.求解功率追踪问题的图论方法[J].电力自动化设备,2002,22(3):12-15.
WU Zhi-gang,ZHANG Yao,SONG Wen-nan,et al.A method to solve power-tracing problem based on graph theory[J].Electric Power Automation Equipment,2002,22(3):12-15.
[15]赵晋泉,黄文英,方朝雄,等.福建电网在线电压稳定监视和控制系统[J].电力系统自动化,2007,31(14):102-106.
ZHAO Jin-quan,HUANG Wen-ying,FANG Zhao-xiong,et al.Fujian on-line voltage stability monitoring and control system[J].Automation of Electric Power Systems,2007,31(14):102-106.

