万向轮螺旋滚子受压变形的有限元分析

谢 霞，严 雷，贾巨民

(1.军事交通学院装运机械系，天津 300161;2.军事交通学院 学员旅，天津 300161)

全方位移动平台是一种可在平面内实现横向运动、纵向运动、斜向运动、旋转运动等全方位移动［1］的机构，在万向叉车、移动机器人等机构中应用广泛［2－6］.由于其转动半径小，运动灵活，非常适于在仓库、舰船、机场等狭小空间内作业.

全方位移动平台的的核心部件是万向轮，它可以使平台实现全方位移动.而万向轮中螺旋滚子的外廓曲线又直接影响运动路线的精准度和运动过程中的平稳度，因此滚子形状对于机构性能有着重大的影响.本文将对螺旋滚子进行有限元仿真，研究滚子在受压情况下的受力分布以及各部分变形量的大小，研究实际廓线与理论廓线之间的关系，为螺旋滚子设计、制造提供理论参考和依据.

1 螺旋滚子简介

螺旋滚子是万向轮的核心组成部分，一般为2个1 对、6 对或9 对组成1 组，均匀斜向分布在轮毂上，其外包络线与整轮的理论圆周相重合.图1为万向轮的结构示意图.滚子轴线与轮毂轴线成一定角度，并且滚子可绕自身轴线旋转.通常4 个这样的万向轮组合在一起，形成全方位移动平台.

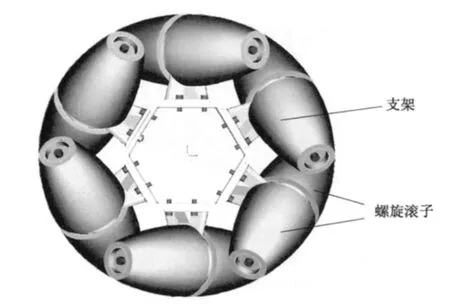
图1 万向轮结构示意图Fig.1 Configuration sketch map of the omni-directional wheel

单个螺旋滚子主要由支架、滚子轴、金属衬套、聚氨酯层、轴承、螺钉等构成，螺旋滚子轴从中间处固定在支架上.图2为1 对滚子的结构图.

图2 螺旋滚子结构示意图Fig.2 Configuration sketch map of the helix roller

当螺旋滚子承受载荷时，其外轮廓面在压力的作用下将发生变形.由此导致实际受载轮廓线和未受载轮廓线之间出现偏离.在螺旋滚子中间处的聚氨酯层在与地面接触时受到的挤压更为显著，形变量也就更大.图3为螺旋滚子变形示意图，其中虚线为理论轮廓线，实线为螺旋滚子受载变形后的实际轮廓线.由于变形使得螺旋滚子侧面轮廓成为并非一个完全闭合的圆，从而导致万向移动平台在运动过程中，出现上下振动的状况，使全移动平台的稳定性降低.因此，需要对变形量进行研究.

图3 螺旋滚子的理论轮廓和实际轮廓示意图Fig.3 Sketch map of actual contour and theoretical contour of the helix roller

2 螺旋滚子受压变形有限元分析的理论基础［7］

有限元法分析基本思路［7］是将螺旋滚子看成由有限个划分的单元组成的整体，每个单元具有简单形态(如四面体或六面体)并通过节点相连，以单元节点的位移作为未知量，将每个单元的刚度矩阵相互结合起来以形成整个模型的总体刚度矩阵，在已知载荷力和约束条件下求解出各个节点的位移.螺旋滚子变形量和各节点载荷的计算过程如下.

系统满足有限元方程:

式中:α 为离散结构点的位移向量;K 和P 分别为离散结构总刚度矩阵和总外力向量.

单元刚度矩阵Ke和单元外力向量Pe的表达式分别为

式中:B 为单元应变－节点位移向量;D 为弹性矩阵;r，θ，z分别为圆柱的径向坐标、转角坐标和轴向坐标;N 为位移内插函数矩阵;Pf为体积力;PS为面积力;S为面积;为单元体积力;为单元面积力.由此可以根据总外力向量和总刚度矩阵求出离散各节点的位移量.

又根据广义虎克定律可以写出应力和应变的关系式:

式中:E为弹性模量;μ 为泊松比;εr和 σr分别为沿半径r方向的正应变和正应力;εθ和 σθ分别为沿 θ方向的正应变和正应力;εz和σz分别为沿z方向的正应变和正应力;γzr为圆柱面zr上沿z，r方向的剪应变;τzr为圆柱面zr上沿z向作用的剪应力.

对于各向同性的材料，令弹性矩阵D 为

即可求出各个节点变形的受力分布.

3 螺旋滚子三维实体模型的建立

将三坐标测量得到的数据在MATLAB 中拟合，建立螺旋滚子的外轮廓面模型，再将这些数据导入到Pro/E 软件中，得到螺旋滚子外轮廓的三维实体模型，如图4所示.

图4 螺旋滚子的三维实体模型Fig.4 Three dimension entity model of the helix roller

通常螺旋滚子成对使用，因此在Pro/E软件中生成滚子对的实体模型.为了研究方便，在螺旋滚子模型下方加一平板，模拟地面.一对螺旋滚子组成的模型如图5所示.

图5 螺旋滚子对三维实体模型Fig.5 Three dimension entity model of the helix roller pairs

4 螺旋滚子受压变形的有限元仿真

4.1 有限元仿真的步骤

应用ANSYS 对螺旋滚子实体模型进行分析，需要完成的工作有:建立螺旋滚子的有限元模型、施加载荷和约束、求解、查看计算结果.

(1)使用ANSYS 软件的 import 命令，将Pro/E软件中的螺旋滚子模型导入到ANSYS 中.

(2)定义单元类型.在ANSYS 软件建模前定义单元类型是必须的，因为单元类型决定了单元的自由度数和单元位于二维空间还是三维空间.ANSYS 软件单元库十分丰富，有超过100 多种适合于不同问题的单元类型.根据装备的结构特点、载荷及约束情况，对螺旋滚子定义了3 种单元类型:shell51 定义板壳单元类型;solid45 和solid65 用于定义三维实体结构类型，其中，solid65 用于模拟三维混凝土模型.

(3)定义实常数.根据实际尺寸，螺旋滚子外廓厚度取0.01 mm.

(4)定义材料参数.对螺旋滚子只考虑线性材料特性，主要输入的是弹性模量和泊松比.根据资料查询，设定螺旋滚子聚氨酯外廓、滚子衬套及内部零件、平板的弹性模量分别是 14.7 MPa，206.0 GPa，44.3 GPa，泊松比分别设定为 0.400，0.300 和 0.244.

(5)给实体模型图元分配单元属性.即为模型的各个区域设置单元属性，从而避免在网格划分过程中出现重置单元.通过 default attribs 命令完成.分别将实体类型、实常数、弹性模量、泊松比分配给对应的模型.

(6)网格划分.通过网格划分连续物体得以离散化，建立螺旋滚子的有限元模型.使用meshtool命令，打开网格划分工具栏.采用系统自动划分的方式进行滚子模型的网格划分.划分后得到的螺旋滚子有限元模型如图6所示.

图6 螺旋滚子的有限元模型Fig.6 Finite element model of the helix roller

(7)创建接触装配.划分后的整个模型由螺旋滚子外廓、螺旋滚子衬套及内部零件、平板等多个部分组成，必须通过创建装配接触使其关联起来，此功能由接触管理器来实现.

(8)加载约束和载荷.通过displacement 命令完成定义约束的功能.设定平板下表面的三个自由度均固定.通过Pressure 命令完成定义载荷功能，设定压力为10 kN，作用在滚子中间的轴承上表面，方向向下，与滚子轴线成60°夹角.

(9)求解.求解的工作主要在求解模块中进行，计算机根据施加给模型的载荷和约束，结合模型的网格划分情况，计算出模型中每个节点的受力和位移情况.ANSYS 中的solve 命令即可完成求解过程.

4.2 仿真结果分析

完成求解过程后，可以通过ANSYS 软件的后处理模块来查看计算所得的结果，常用的有变形图、位移云图、应力云图等.如图7所示为螺旋滚子受力变形图，图中虚线为受力变形前的轮廓线，实线为变形后的轮廓线.节点单元位移云图如图8所示.

图7 螺旋滚子的受力变形图Fig.7 Deformation chart of the helix roller under the press load

图8 节点单元位移云图Fig.8 Displacement nephogram of the node cell

(1)螺旋滚子与地面的有效接触面积比较小，一方面使得滚子作用力集中，容易造成滚子外层的损坏;另一方面与地面摩擦力较小，容易造成打滑现象.为避免螺旋滚子与地面发生打滑，需要滚子外层表面粗糙度要大，以增大摩擦力;另外，要求外层材料具有较高的硬度，以满足耐磨损的要求.实践中也证明，滚子的外层最容易磨损，需要经常更换.实际中通常使用的材料为聚氨酯，基本能满足上述要求.当然，开发更为理想的材料仍是研究人员的目标之一.

(2)螺旋滚子在受压后将产生变形，在滚子的轴线方向和垂直方向都会产生位移，这会降低全方位平台运行的平稳性和精度.通过仿真得到的变形数据，可以看出，滚子轴线即x轴方向上的最大位移量为3.12 mm，发生在y轴坐标最大的节点处.垂直最大位移即y轴方向上的最大位移为5.47 mm，发生在滚子横坐标方向中间部位.因此，需要在滚子的受力集中部位，如轴承、衬套处选择强度较大的材料.

(3)经过有限元分析可以得出，螺旋滚子在受压变形时，实际轮廓线会偏离理论轮廓线，但偏离量不大.要保证全方位移动平台运行的平稳性和运动路线的精确性，就需要保证滚子变形后的外包络线与整轮的理论圆周相重合.因此在滚子设计时，必须考虑受力变形的影响.

5 结论

通过对万向轮螺旋滚子进行三维实体建模和受力变形的有限元仿真，找到了滚子在轴线方向和垂直方向的最大位移处，并得到了滚子在受压变形下，实际轮廓线和理论理想轮廓线的偏移.分析结果有助于提高全方位移动平台的运动精度，并使其更好地推广应用.

影响螺旋滚子变形情况的因素很多，既有螺旋滚子本身的影响，包括螺旋滚子的尺寸、材料、布置方式、轮子轴与螺旋滚子轴之间的夹角等，同时又取决于外力大小、外力方向、模拟地面的各种参数等因素.后续需要对滚子的不同模型以及整个万向轮进行静力学和动力学仿真分析，找出最合理的参数，以便对螺旋滚子进行优化设计或改进.

［1］关利赢，郝鑫，常力欣.万向电动叉车螺旋滚轮轮体设计［J］.军事交通学院学报，2009，11(2):65－68.GUAN Liying，HAO Xin，CHANG Lixin.Design of mecanum wheels of omni-directional electric forklift ［J］.Journal of Academy of Military Transportation，2009，11(2):65－68.

［2］仲欣，吕恬生.在球面运行的万向轮式移动机器人运动学模型的建立［J］.机器人，1999，21(3):184－190.ZHONG Xin，LV Tiansheng.Kinematic modeling of omnidirectional wheeled mobile robots running on spherical surfaces［J］.Robots，1999，21(3):184－ 190.

［3］贾茜，王兴松，周婧.基于多种控制方式的全方位移动机器人研制［J］.电子机械工程，2010(4):61－64.JIA Qian，WANG Xingsong，ZHOU Jing.Development of omnidirectional mobile robots based on several control modes［J］.Electro-Mechanical Engineering，2010(4):61－ 64.

［4］高学山，徐殿国，王炎，等.全方位地面移动清扫机器人［J］.机械工程学报，2008，44(3):228－233.GAO Xueshan，XU Dianguo，WANG Yan，et al.Omni-directional mobile robot for floor cleaning［J］.Chinese Journal of Mechanical Engineering，2008，44(3):228－ 233.

［5］石维亮，王兴松，贾茜.基于Mecanum 轮的全向移动机器人的研制［J］.机械工程师，2007(9):18－21.SHI Weiliang，WANG Xingsong，JIA Qian.Development of omnidirectional mobile robot based on mecanum wheel ［J］.Mechanical Engineerer，2007(9):18－21.

［6］闫国荣，张海兵.一种新型轮式全方位移动机构［J］.哈尔滨工业大学学报，2001，33(6):854－857.YAN Guorong，ZHANG Haibing.A new kind of wheel-model all directional moving mechanism［J］.Journal of Haebin Institute of Technology，2001，33(6):854－857.

［7］任明法.具有金属内衬复合材料缠绕结构成型和使用过程的一体化分析［D］.大连:大连理工大学，2005.REN Mingfa.Integration analysis of filament wound composite structure forming with metal liner and using process［D］.Dalian:Dalian University of Technology，2005.