基于B样条本征时间尺度分解和对角切片谱的轴承故障诊断

钟先友，曾良才，赵春华，陈保家

滚动轴承是机械设备中最常用的、最易损伤的零部件之一，其状态监测和故障诊断一直受重视。滚动轴承发生故障时，其振动信号通常表现出非线性、非平稳特征。在目前的非平稳信号处理方法中，常用于滚动轴承故障诊断的方法有小波变换［1-2］、经验模式分解(Empirical Mode Decomposition，EMD)［3-5］和局部均值分解(Local Mean Decomposition，LMD)［6-7］。但是这些方法都存在着一定的局限性，其中小波变换需要选择基函数和分解层数，因而对信号的处理缺乏自适应性;EMD存在过包络、欠包络、模态混淆、端点效应等问题。LMD也存在迭代计算量大、模态混淆、端点效应等问题。

Frei等［8］提出了一种自适应时频分析方法—本征时间尺度分解方法(ITD)，并将这种方法应用于生物医学信号处理中，取得了较好的效果。ITD方法能够自适应地将一个复杂信号分解为若干个瞬时频率具有物理意义的PR分量之和。与EMD相比，ITD在计算效率方面有明显优势，适合在线分解。林近山［9］将ITD算法成功地应用于齿轮箱的故障诊断中。但是ITD方法中对基线的定义是基于信号本身的线性变换，因此从第二个分量开始，有明显的信号失真。郑进德和杨宇等［10-11］采用三次样条插值对ITD方法进行改进并应用到轴承和转子的故障诊断中。但三次样条拟合曲线时会产生的过包络、欠包络问题［12］，文献［12-13］采用B样条插值分别改进EMD和LMD算法，并验证了B样条插值的优越性。因此，本文提出了B样条插值改进的本征时间尺度分解方法(BITD)。

Teager能量算子适合检测轴承振动信号中的冲击成分，对信号的瞬时变化具有良好自适应能力，而且计算复杂性低，计算效率高。文献［4，14］运用Teager能量算子成功地识别出滚动轴承的故障特征频率。

包络分析技术是轴承故障振动信号分析的最有效方法之一。在进行包络分析之前，为了消除噪声的干扰，须先对振动信号进行高通滤波，以消除低频噪声的干扰，但高频滤波的中心频率和带宽往往难以选择，滤波参数的选择对分析结果影响很大［15］。滚动轴承发生故障时产生的周期性冲击引起轴承系统的高频固有振动，故障特征被调制到高频段，采用BITD方法将轴承振动信号分解为若干个PR分量，这些分量由高频到低频依次被分解出来，选取分解结果的前几个分量重构就可能突出故障信号的高频段，从而克服了包络分析需要预先确定滤波器中心频率和带宽的难题。

实际轴承振动信号中往往混入了大量的噪声，使得原始故障特征信息与噪声混淆而不易提取，对角切片谱具有抑制高斯白噪声的特性，同时可以识别轴承振动信号中的二次相位耦合成分［16］。

基于以上原因，本文提出了基于B样条的本征时间尺度分解、Teager能量算子解调和对角切片谱相结合的轴承故障诊断方法，成功地提取出滚动轴承的故障特征。

1 ITD方法

ITD方法能够自适应地将一个复杂信号分解为若干个相互独立的合理旋转分量和一个趋势项之和。设Xt是待分析的原信号，分解前先定义一个基线提取算子L，使得从原始信号中去掉该基线后剩下的余量信号成为一个合理旋转分量。一次分解的表达式为［8］:

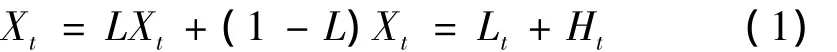
(1)确定信号Xt的极值点Xk及对应的时刻τk(k=1，2，…M，M为所有极值点的个数)，并计算

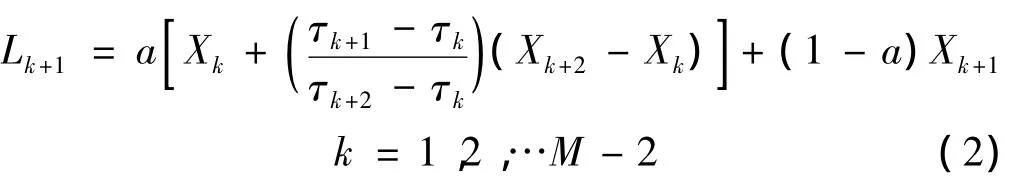
式中:0 ＜a＜1，一般地，a=0.5。

(2)定义信号的分段线性基线提取算子如下:

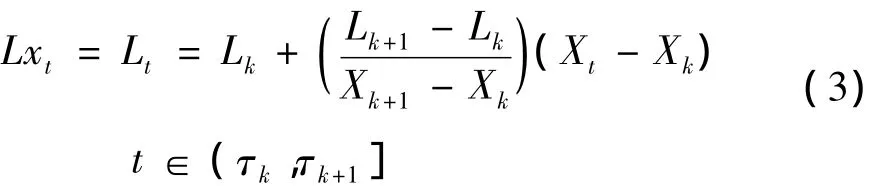
(3)将基线信号Lt作为原始信号，重复上述步骤，直到基线信号为一单调函数或常函数。原始信号被分解为:

考察式(5)所示信号

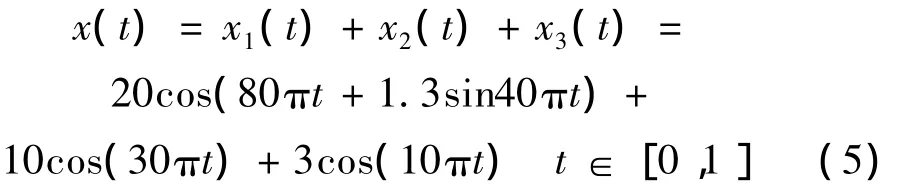
式中:x1(t)为调频信号，x2(t)和x3(t)为两个余弦信号，时域波形如图1。对x(t)别进行ITD分解，得到的分解结果如图2所示，其中PR1、PR2和PR3分别为ITD分解的前三个分量，R为残余分量。

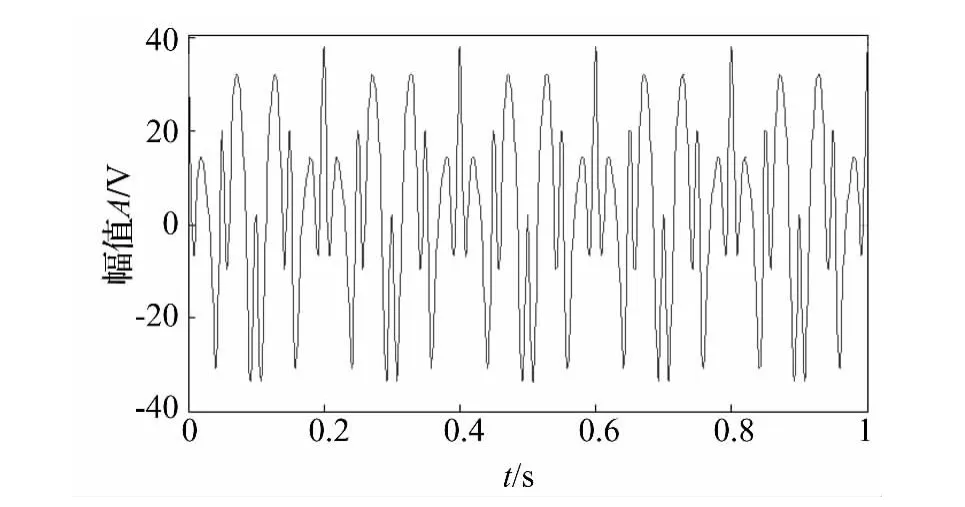
图1 仿真信号的时域波形Fig.1 The time domain of simulated signal

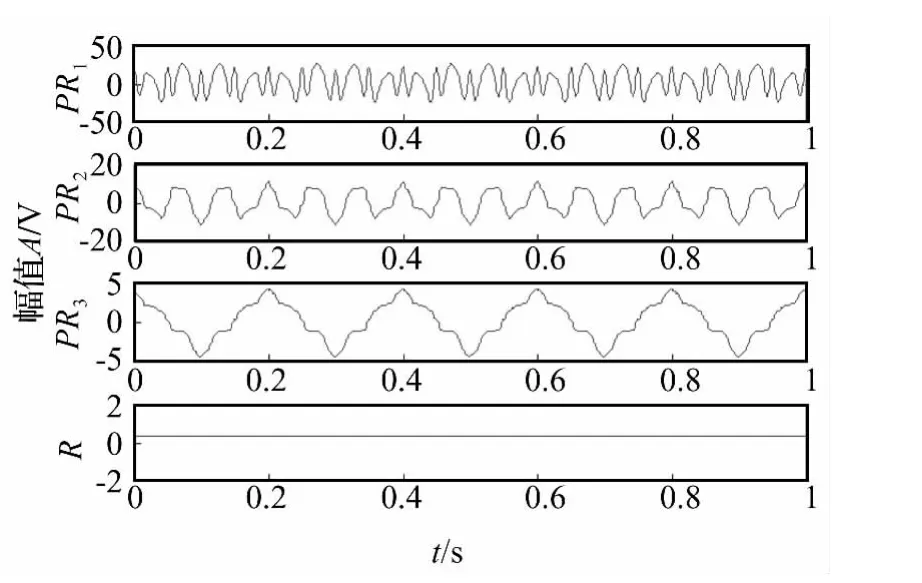
图2 仿真信号的ITD分解结果Fig.2 ITD decomposition results of the simulation signal

从图2中可以看出，PR1分量、PR2分量和PR3分量分别对应于仿真信号x(t)的三个分量x1(t)、x2(t)和x3(t)，第二个分量和第三个分量出现了失真，这是由于ITD方法中是以原始信号任意两个相邻的极值点为跨度对信号进行分段线性变换来构造基线信号，这导致第二个分量和第三个分量信号波形出现了毛刺而失真。因此，本文对ITD方法进行改进，用B样条插值来代替ITD方法中的线性变换。

2 BITD方法

BITD方法基本的分解过程如下:

(1)确定原始信号Xt所有的局部极值点，方法与ITD相同，通过式(2)和(3)和计算各基线的控制点Xk。

(2)对序列端点采用镜像对称延拓方法进行延拓，得到左右两端点极值(τ0，X0)和(τM+1，XM+1)，令 k 分别等于0和M，按式(2)求出L1与LM的值，然后对所有Lk用B样条函数来拟合，得到基线信号L1。

(3)将L1从原始信号中分离出来，得到P1，若P1是一个PR分量，则P1作为信号Xt的第一个分量，否则将P1作为原始信号重复上述步骤，循环k次，直到得到Pk是一个PR分量，Pk即为信号Xt的第一个PR分量PR1，将PR1信号中分离出来，得到一个新的信号r1。

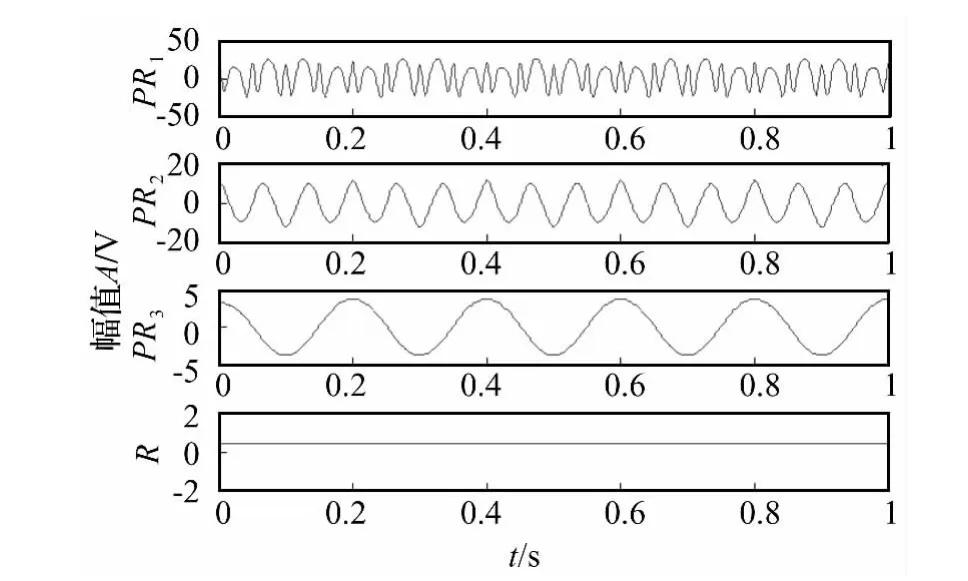
图3 仿真信号的BITD分解结果Fig.3 BITD decomposition results of the simulation signal

(4)再将r1作为原始信号重复上面的步骤，得到Xt的第二个满足条件的PR2。重复循环n次，得到信号Xt的n个满足PR条件的分量，直到rn为一单调函数或常函数，这样就把Xt分解为n个PR分量和一个单调或常函数之和，即:

用BITD方法对图1仿真信号x(t)进行分解，得到的分解结果如图3所示，从图中可以看出，BITD方法对第二个分量和第三个分量的分解也取得较好的效果。

文献［12］采用B样条插值改进EMD算法，简称BEMD，现对于图1所示的信号，分别用EMD、BEMD、ITD和BITD进行分解，比较四者的分解效果，在同一台电脑上，各运行20次，取平均值，得到三种方法分解的时间用t来表示，用r1和r2表示分解得到的第一个分量和第二个分量与真实信号的相关系数。结果与表1所示。

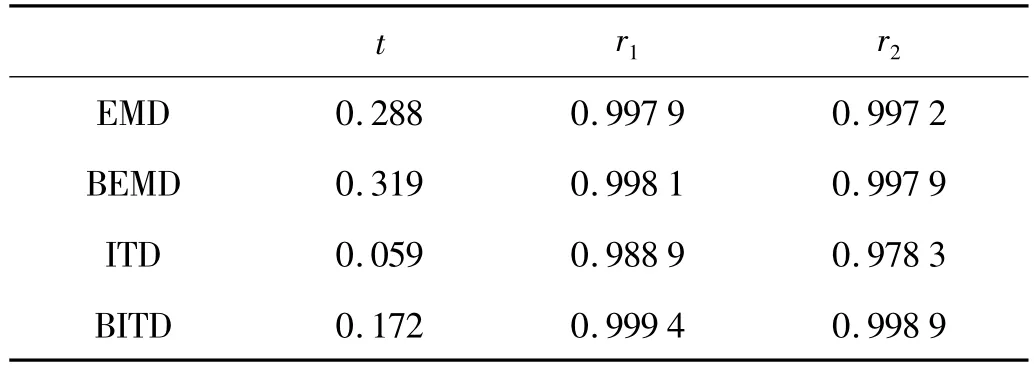
表1 四种方法分解效果比较Tab.1 Comparison of four methods of decomposition

从表1可以看出，ITD分解速度最快，但分解所得的分量与真实分量的相关性最小，而BITD分解速度比EMD和BEMD快，且分解所得的分量与真实分量的相关性最大，相比另外三种分解方法具有一定的优势。

3 Teager能量算子的基本原理

Teager能量算子计算简单，计算效率高。在机械故障诊断中，能量算子解调方法被用于处理振动信号来提取故障信息［4，14］。连续信号 x(t)的 Teager能量算子可定义为:

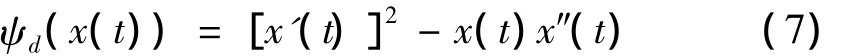
式中:x(t)为测得振动信号，x'(t)和x″(t)分别为信号x(t)的一阶和二阶导数。

离散信号x(n)的Teager能量算子可定义为:

对于离散时间信号，能量算子只需要三个样本数据就可以计算任意时刻n处的信号源能量。

4 对角切片谱的基本原理

轴承发生故障时，系统会表现出一定的非线性，最常见的表现形式就是二次相位耦合。对于这种非线性耦合现象，仅用基于二阶统计量的分析方法如自相关、功率谱来处理，很难将故障特征提取出来，这主要是由于二阶统计量不提供任何相位信息。对角切片谱能检测二次相位耦合特征，并且当信号中混有高斯噪声时，理论上可被对角切片谱完全抑制掉。

对于随机变量 x(t)，它的三阶累积量 c3x(τ1，τ2)(τ1、τ2为时间延迟)的对角切片为 c3x(τ，τ)，定义该对角切片的傅里叶变换为随机变量x(t)的对角切片谱:

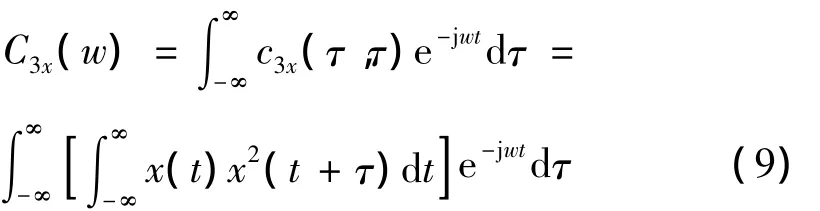
5 基于BITD、能量算子和对角切片谱的诊断方法

将基于BITD、Teager能量算子和对角切片谱的诊断方法应用到滚动轴承诊断中，主要包括以下步骤:

(1)对信号x(t)进行BITD分解，得到若干个PR1，PR2…PRn分量;

(2)计算各PR分量与原信号的相关系数;

(3)计算各PR分量的样本熵;

(4)取相关系数和样本熵值都较大的PR分量重构信号，对重构信号进行能量算子解调并求对角切片谱。重构的分量个数要通过分析来取值，本文取相关系数大于0.3和样本熵值大于1的PR分量重构信号。

6 轴承故障仿真信号分析

根据文献［17］建立滚动轴承元件发生单点局部损伤时传感器所采集到的信号模型为:

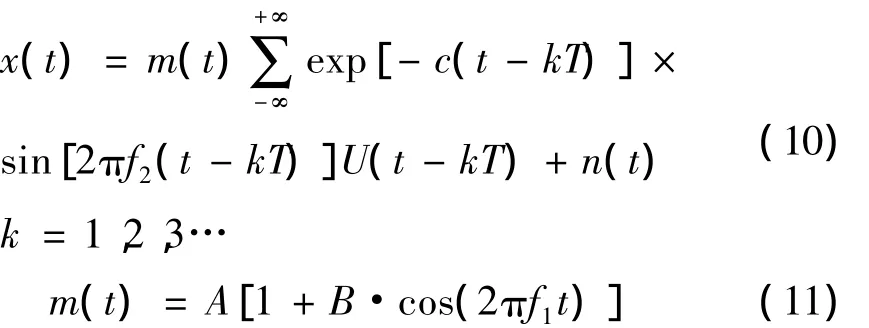
其中:m(t)是冲击幅值，是幅值调制函数;f1是第一调制频率，等于轴的转频或滚动体的公转频率;T为故障特征周期;f2是轴承座-传感器系统的某一固有频率，即载波频率;c为冲击信号衰减指数;U(t)为单位阶跃函数;n(t)为噪声。其中取固有频率f2为2.5 kHz，阻尼系数为c=0.1，n(t)=0，T=1/200，m(t)=1。根据式(10)和式(11)可得到外圈故障的时域波形和频谱图如图4。向信号中添加Gauss白噪噪声，使得信噪比为-10 dB，得到外圈故障的时域波形和频谱图如图5和图6。

图5 加噪后轴承故障模拟信号的时域图Fig.5 The time domain of simulate bearing failure signal with noise

采用BITD方法对该故障仿真信号进行分解，得到8个PR分量和一个残余分量，前4个分量如图7所示，计算前3个PR分量与原信号的相关系数和PR分量的样本熵，如表2所示。

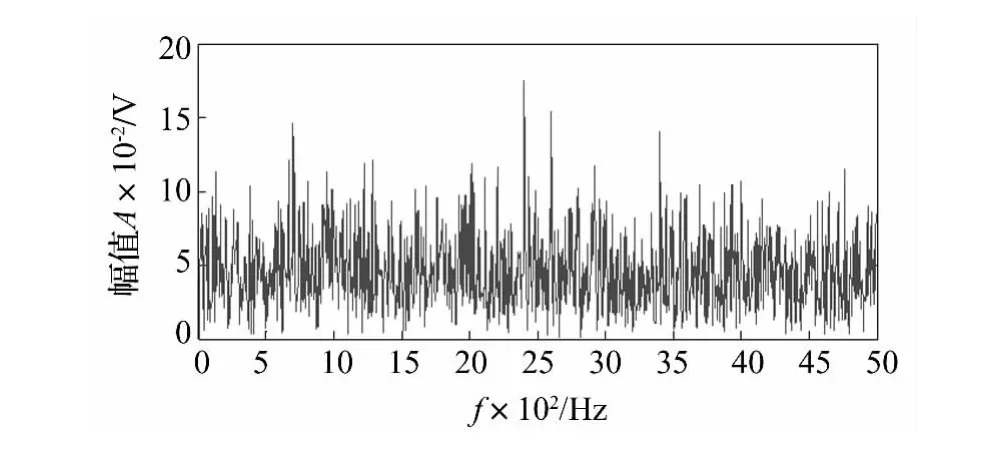
图6 加噪后轴承故障模拟信号的频谱图Fig.6 The frequency domain of simulate bearing failure signal with noise

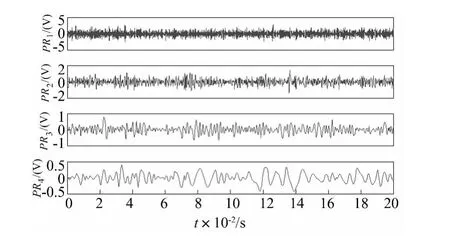
图7 BITD方法对图5中轴承信号的分解结果Fig.7 The decomposed results of bearing signal shown in Fig.5 by BITD

表2 PR分量与原信号的相关系数及样本熵Tab.2 The correlation coefficients between PR andoriginal signal，and the PR sample entropy

从表2看出，前两个分量相对较大，对前两分量进行重构，得到分量PR12，计算PR12分量与原信号的相关系数和样本熵，其值分别为0.82和1.32，PR12相比单个PR分量提高了相关系数和样本熵值，保留了原始信号更多的冲击特征信息，故对PR12分量进行能量算子解调后求对角切片谱，结果如图8。从图8中可以清楚地看出，在故障特征一倍频(200 Hz)及其倍频处有明显的谱线，表明本文提出的方法可以将故障频率成分成功地提取出来。

为了进行对比分析，对原信号进行Hilbert变换求包络谱，如图9所示，在包络谱中可以找到故障特征频率一倍频(200 Hz)，但故障特征频率二倍频和三倍频无法识别，说明本文所提方法效果更好。

对PR12分量进行Hilbert变换求包络谱，如图10所示，在包络谱中可以找到故障特征频率一倍频(200 Hz)和故障特征的三倍频，对比图9和图10可知，可以看出，经BITD分解后作包络谱分析，可以进一步削弱部分干扰成分，提高信噪比，而与图8比较，可以看出本文提出的方法分析结果更为准确，信噪比更高。

图8 PR12分量的对角切片谱Fig.8 Diagonal slice spectrum of PR12 component

图9 图5中轴承信号的包络谱Fig.9 The envelope spectra of bearing signal shown in Fig.5

图10 PR12分量的包络谱Fig.10 The envelope spectra of PR12 component

7 发电机滚动轴承故障诊断实例

图11是某公司850 kW发电机轴承振动信号的时域波形及频谱。轴承故障为外圈损伤，轴承型号6326，采样频率25 600 Hz。转频为24.33 Hz，轴承外圈故障特征频率为85.8 Hz。从图11可以看出，时域波形比较复杂，难以分辨出信号的具体特征。在频谱图中，故障信号的低频特征淹没在背景噪声中，无法识别故障频率及其谐波。

图11 轴承振动信号时域图和频谱Fig.11 The time domain and frequency domain of bearing vibration signal

采用BITD方法对该故障仿真信号进行分解，得到10个PR分量和一个残余分量，前3个分量如图12所示，计算PR与原信号的相关系数和PR的样本熵，如表3所示。

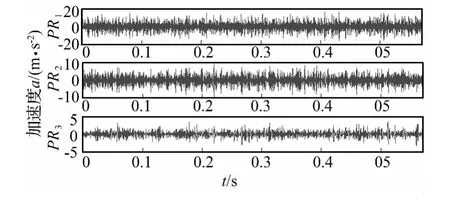
图12 BITD方法对轴承信号的分解结果Fig.12 The decomposed results of bearing signal by BITD

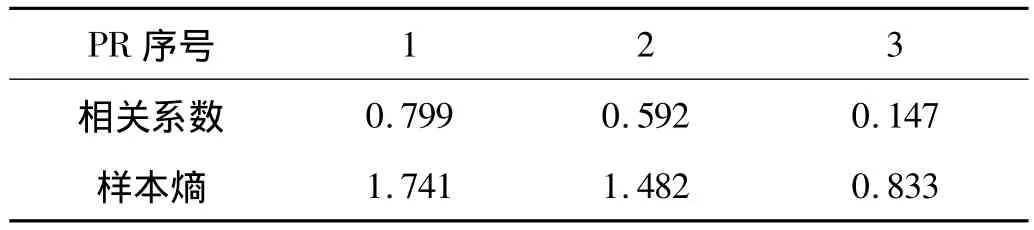
表3 PR分量与原信号的相关系数及样本熵Tab.3 The correlation coefficients between PR and original signal，and the PR sample entropy

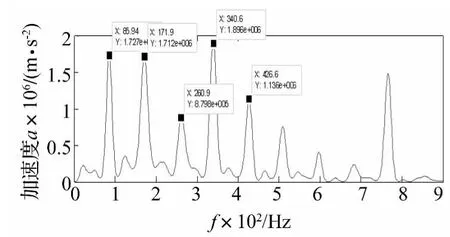
图13 PR12分量的对角切片谱Fig.13 Diagonal slice spectrum of PR12 component

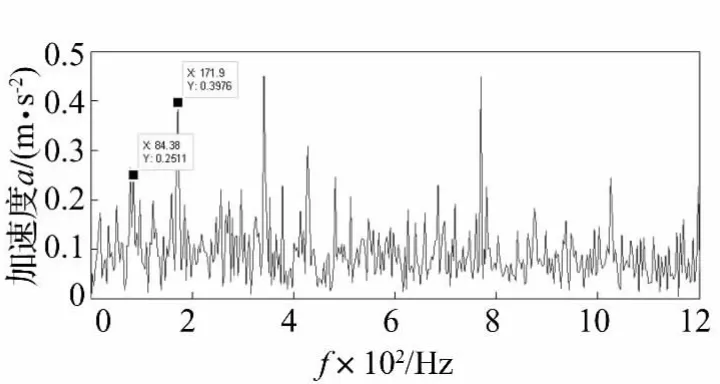
图14 PR12分量的包络谱Fig.14 The envelope spectra of PR12 component

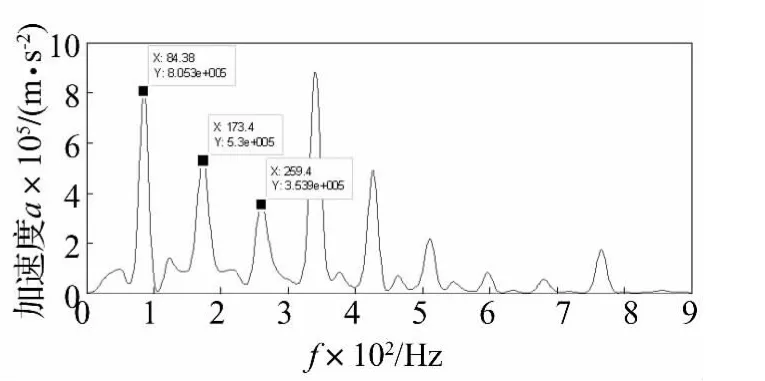
图15 重构信号的对角切片谱Fig.15 diagonal slice spectrum of the reconstruction signal

从表3看出，前两个分量相对较大，对前两分量进行重构，得到分量PR12，计算PR12分量与原信号的相关系数和样本熵，其值分别为0.961和2.103，PR12相比单个PR分量提高了相关系数和样本熵值，故对PR12分量进行能量算子解调后求对角切片谱，结果如图13。从图中可以清楚地看出，在故障特征一倍频、二倍频和三倍频处有明显的谱线，表明本文所提出的方法可以将故障频率成分成功提取出来。

对PR12分量进行Hilbert变换求包络谱，如图14所示，在包络谱中可以找到与故障特征频率一倍频(85.8 Hz)相近的频率和故障特征的二倍频，但一倍频处存在干扰成分，且故障特征的三倍频无法识别，对比图13和图14可知，可以看出本文所提出的方法的分析结果更为准确，信噪比更高。

对振动信号进行EMD分解，求各分量与原信号的相关系数及样本熵，前两个分量IMF1和IMF2与原信号的相关系数大于0.3，样本熵值大于1，故对前两分量进行重构，对重构信号进行能量算子解调后求对角切片谱，结果如图15。从图15中可以看出，在故障特征一倍频(85.8 Hz)、二倍频和三倍频附近处有较明显的谱线，但频率值没有图13中的准确，且图13中二倍频更为明显，表明本文所提出的方法识别效果更好。

8 结论

(1)本文所提出的BITD方法是一种自适应时频分析方法，可以解决ITD方法分解信号产生的波形失真问题;

(2)比较对原信号直接做包络谱分析和对信号进行BITD分解后作包络谱分析的效果，结果表明BITD分解可以削弱部分干扰成分，提高信噪比，但与本文所提出的方法相比，基于BITD、Teager能量算子和对角切片谱的分析结果更为准确，信噪比更高;

(3)BITD方法计算效率高，能量算子解调和对角切片谱，快速，易于实现，仿真信号与轴承故障诊断工程实例的分析表明，本文所提出的方法能有效地提高信噪比，突出故障特征，提高故障诊断的准确性，具有良好的应用前景。

［1］王晓冬，何正嘉，訾艳阳.滚动轴承故障诊断的多小波谱峭度方法［J］.西安交通大学学报，2010，44(3):77-8 WANG Xiao-dong，HE Zheng-jia，ZI Yan-yang.Spectral kurtosis of multiwavelet for fault diagnosis of rolling bearing［J］.Journal of Xi'an Jiaotong University，2010，44(3):77-81.

［2］彭志科，何永勇，褚福磊.小波尺度谱在振动信号分析中的应用研究［J］.机械工程学报，2002，38(3):122-126.PENG Zhi-ke，HE Yong-yong，CHU Fu-lei.Using wavelet scalogram for vibration signals anaylsis［J］.Chinese Journal of Mechanical Engineering，2002，38(3):122-126.

［3］汤宝平，蒋永华，张详春.基于形态奇异值分解和经验模态分解的滚动轴承故障特征提取方法［J］.机械工程学报，2010，46(5):37-42.TANG Bao-ping，JIANG Yong-hua， ZHANG Xiang-chun.Feature extraction method of rolling bearing fault based on singular value decomposition-morphology filter and empirical mode decomposition［J］.Chinese Journal of Mechanical Engineering，2010，46(5):37-42.

［4］李 辉，郑海起，杨绍普.基于EMD和Teager能量算子的轴承故障诊断研究［J］.振动与冲击，2008，27(10):15-22.LI Hui， ZHENG Hai-qi， YANG Shao-pu. Bearing fault diagnosis based on EMD and teager kaiser energy operator［J］.Journal of Vibration and Shock，2008，27(10):15-22.

［5］苏文胜，王奉涛，张志新，等.EMD降噪和谱峭度方法在滚动轴承早期故障诊断中的应用［J］.振动与冲击，2010，29(3):18-21.SU Wen-sheng，WANG Feng-tao，ZHANG Zhi-xin，et al.Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings［J］.Journal of Vibration and Shock，2010，29(3):18-21.

［6］程军圣，杨 怡，杨 宇.基于LMD的能量算子解调机械故障诊断方法［J］.振动、测试与诊断，2012，32(6):915-918.CHENG Jun-sheng，YANG Yi，Yang Yu.Energy operator demodulation mechanical fault diagnosis method based the LMD ［J］.Journal of Vibration，Measurement ＆ Diagnosis，2012，32(6):915-918.

［7］杨 宇，王欢欢，程军圣，等.基于LMD的包络谱特征值在滚动轴承故障诊断中的应用［J］.航空动力学报，2012，27(5):1153-1158.YANG Yu，WANG Huan-huan，CHENG Jun-sheng，et al.Application of envelope spectrum characteristics based on LMD to roller bearing fault diagnosis［J］.Journal of Aerospace Power，2012，27(5):1153-1158.

［8］Frei M G，Osorio I.Intrinsic time-scale decomposition:analysis and real-time filtering of non-stationary signals［J］.Proceedings of the Royal Society，2007，463:321-342.

［9］林近山.基于本征时间尺度分解算法的齿轮箱故障诊断［J］.机械传动，2011，35(9):51-53.LIN Jin-shan.Fault diagnosis of gear box based on Intrinsic time-scale decomposition algorithm［J］.Journal of Mechanical Transmission，2011，35(9):51-53.

［10］郑近德，程军圣，杨 宇.基于改进的ITD和模糊熵的滚动轴承故障诊断方法［J］.中国机械工程，2012，23(19):2372-2377.ZHENG Jin-de，CHENG Jun-sheng，YANG Yu.A rolling bearing fault diagnosis method based on improved ITD and fuzzy entropy ［J］.Chinese Mechanical Engineering，2012，23(19):2372-2377.

［11］杨 宇，王欢欢，程军圣.基于ITD改进算法和关联维数的转子故障诊断方法［J］.振动与冲击，2012，31(23):67-70.YANG Yu，WANG Huan-huan，CHENG Jun-sheng.A rotor fault diagnosis method based on ITD improved algorithm and correlation dimension ［J］.Journal of Vibration and Shock，2012，31(23):67-70.

［12］邱绵浩，刘 箐，丛 华.基于B样条插值曲线直接筛选的EMD及其在机械振动信号处理中的应用［J］.装甲兵工程学院学报，2007，21(3):29-33.QIU Mian-hao，LIU jing，CONG Hua.Research of direct sifting EMD based on cubic B-Spline interpolation curve and its application in processing mechanical vibrating signals［J］.Journal of Academy of Armored Force Engineering，2007，21(3):29-33.

［13］王明达，张来斌，梁 伟，等.基于B样条插值的局部均值分解方法研究［J］.振动与冲击，2010，29(11):73-77.WANG Ming-da，ZHANG Lai-bin，LIANG Wei，et al.Local mean decomposition method based on B-spline interpolation［J］.Journal of Vibration and Shock，2010，29(11):73-77.

［14］王天金，冯志鹏，郝如江，等.基于Teager能量算子的滚动轴承故障诊断研究［J］.振动与冲击，2012，31(2):1-5.WANG Tian-jin，FENGZhi-peng，HAORu-jiang，et al.Fault diagnosis of rolling element bearings based on Teager energy operator［J］.Journal of Vibration and Shock，2012，31(2):1-5.

［15］高 强，杜小山，范 虹，等.滚动轴承故障的EMD诊断方法研究［J］.振动工程学报，2007，20(1):15-18.GAO Qiang，DU Xiao-shan，FAN Hong，et al.An empirical mode decomposition based method for rolling bearing fault diagnosis［J］.Journal of Vibration Engineering，2007，20(1):15-18.

［16］ Kachenoura A，Albera L，Bellanger J J，et al.Nonminimum phase identification based on higher order spectrum slices［J］.IEEE Transaction on Signal Processing，2008，56(5):1821-1829.

［17］Mc Fadden PD，Smith JD.Model for the vibration produced by a single point defect in a rolling element bearing［J］.Journal of Sound and Vibration，1984，96(1):69-82.