实体建模三角网相交算法及应用研究

王喜贤

(辽宁工程技术大学研究生学院，辽宁 阜新 123000)

0 引言

在露天矿开采计划中，需要分期分批地处理对地层的剥离操作。如何定位采场工作面、坡顶坡底线和境界位置，并计算每一批次的土、岩和煤量，这些都是亟待解决的问题。通常应用计算机图形辅助设计软件，采用构造实体的方法对矿山地质地层建立数字模型，通过实体间的布尔运算(并、交、差)来演示动态开采和计算剥离量。

1 理论研究

张少丽等对包围盒判断三角形面元方法进行了改进，剔除部分无效三角形，提高了模型求交效率［4］，提出一种优化算法，使之能够更加精确地确定三角形面元所占的空间网格［5］。初剑、魏志强等提出了“带权曲面边界延伸方法”［6］，有效解决了因采样数据点不足所导致的几何交线与曲面分析结果不一致的情况。尹长林、喻定权从图形拓扑结构角度，给出一种基于拓扑搜索的三角网求交算法［7］，该算法引入空间辅助网格对原始三角网中的三角形进行筛选，并在候选三角形集合中依次追踪、计算构成交线的交线线段，在获得每个交线线段的同时完成了线段之间的连接。在对三角形面元对求取交线段阶段，Tomas Moller研究提出的快速三角形相交检测算法［8］最为经典。Oren Tropp利用公共元素和线性矩阵减少了三角形相交判断的运算操作次数，仅需要三次求解方程，得到的结果亦完全包含了相交测试判断［9］。

空间不规则三角网求交即是根据地质采样点数据构建不规则三角网模型，并对地形模型表面格网进行求交计算，生成模型间相交部分的边缘线的过程。通过相交算法求取的交线能够准确表达工程位置边界线，继而与表面格网形成无缝包络面，把三维实体运算转化为二维面运算，快速得到所需工程量。

2 矿区地形三维建模

采用三角网生长算法构建带约束条件的CD－TIN模型，根据以上算法编写VBA过程，载入数据点，所得TIN模型如下图所示。应用AUTOCAD软件完成构建矿区地形TIN模型过程后，得到由若干三维多段线组成的三角网结构，经过TIN模型求交预处理采用包围盒方法排除完全不相交的三角形单元避免无效检测。运用除数留余法建立Hash表，进一步剔除部分肯定不相交的三角形，大大提高了求交效率。TIN模型交线求取利用Tomas Moller研究提出的快速三角形相交检测算法进而判断三角形是否相交。

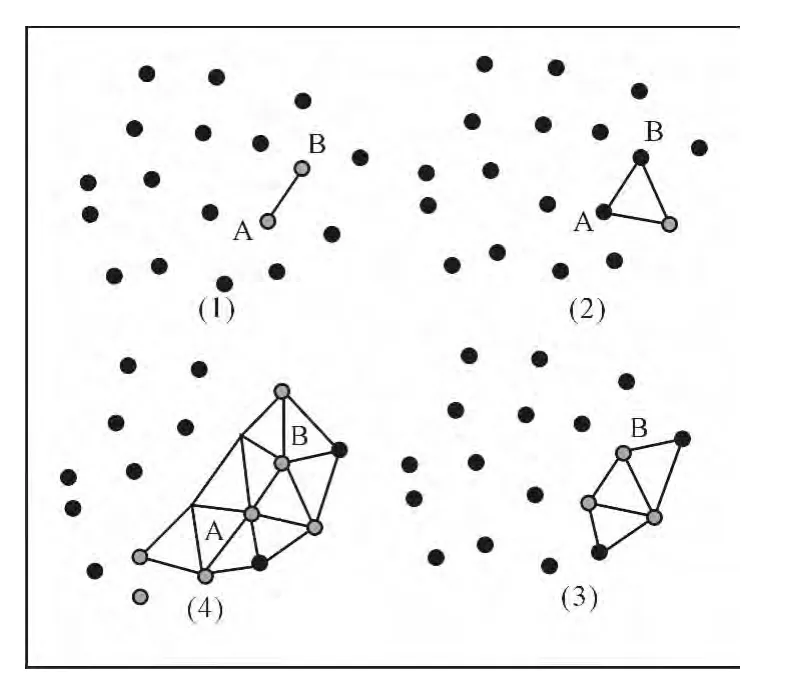
图1 三角网生长算法示意图

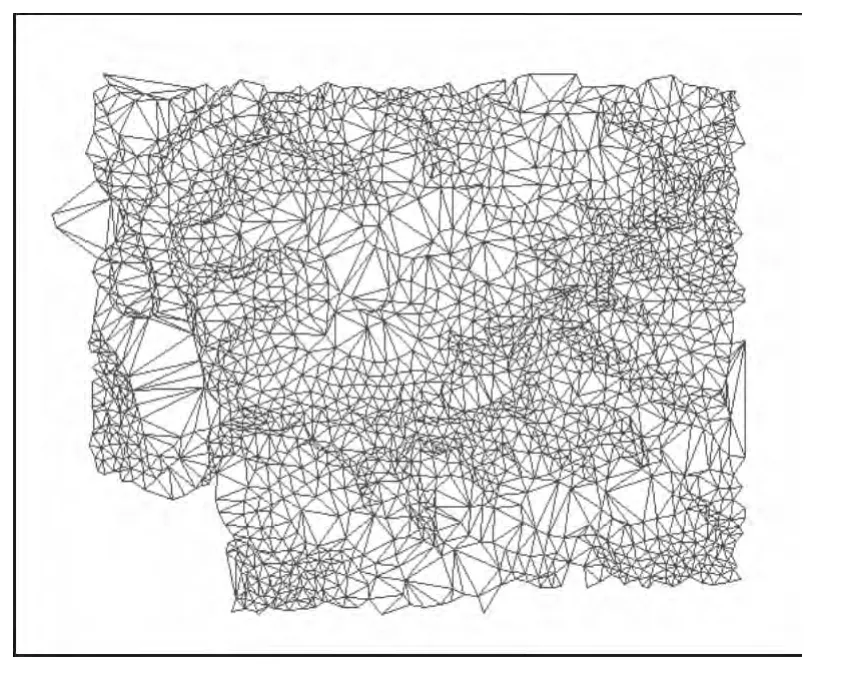
图2 TIN模型

3 绘制交线

在三维面环境下，有两地表TIN三维面模型，求两三角网的交线。

4 实例研究

利用以上所述算法编写的程序，黑岱沟露天煤矿构建了露天矿地形模拟TIN模型，并给出了计划采掘边界线。

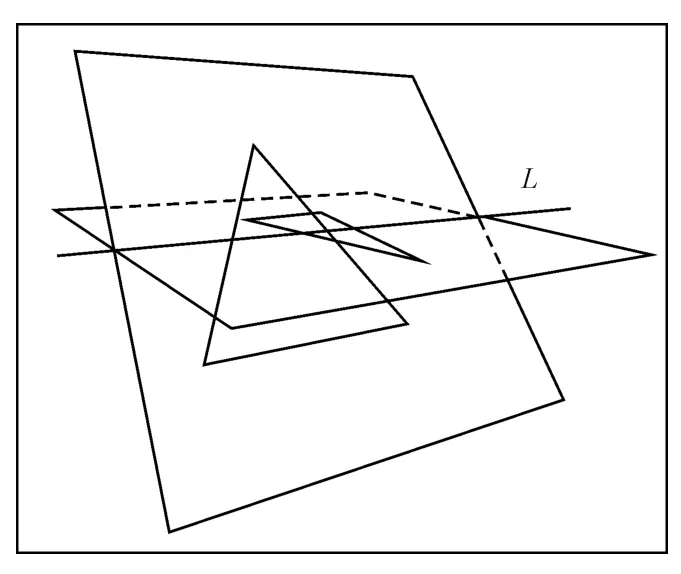
图3 三角形及其平面相交情形1

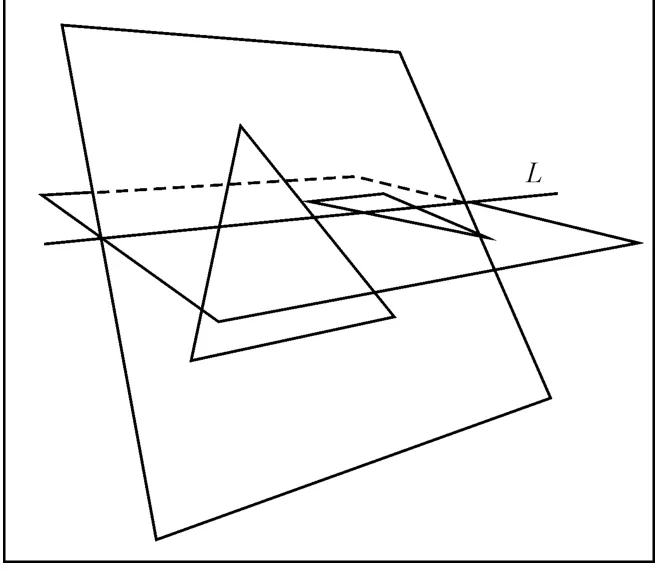
图4 三角形及其平面相交情形2

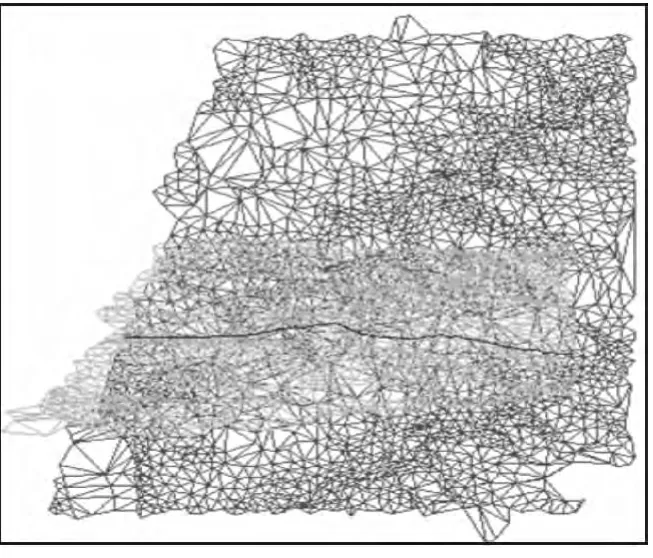
图5 TIN三维线模型交线

图6 TIN三维线模型交线

图6 TIN三维面模型交线

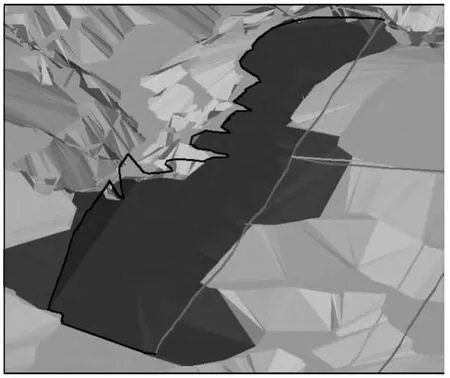
图7 更新后的地形DEM

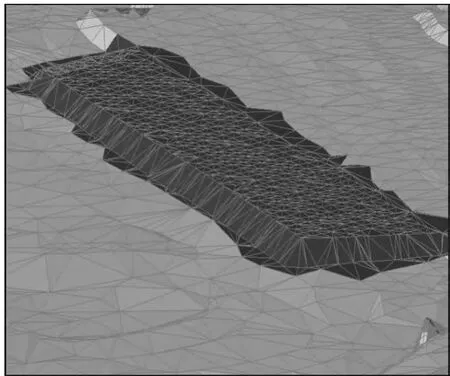
图8 更新后的排土场DEM

5 结论

本文以求取不规则三角网模型交线的目的，深入分析了矿区地形TIN模型的建立方法，先后利用包围盒方法与空间分解法对TIN模型的三角形单元进行预处理，最终绘制出快速准确的模型间交线位置，得出以下部分结论:

(1)利用VBA语言实现三角网生长算法构网，能够生成带约束线的CD－TIN，地形模拟效果较好，但构网速度较慢。

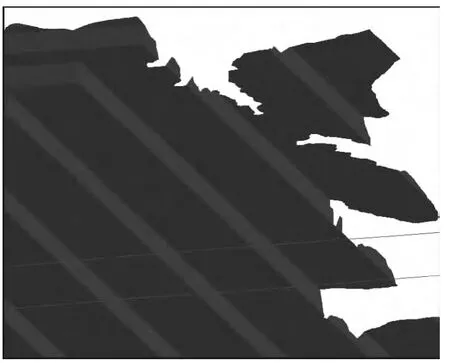
图9 裁剪后的长期计划DEM

(2)采取改进的包围盒算法确定TIN模型可能相交空间范围。

(3)根据空间分解法对相交范围进行空间格网编码，提高重合部分较大的模型间的求交运算效率。

(4)鉴于模型交线段的连续性，采用线段寻址算法对端点坐标排序，得到较为吻合的交线段连线。

［1］Brassel K E and Reif D.Procedure to generathissen polygons［J］.Geographical Analysis.1979，11:289 －303.

［2］Mc Cullagh M J and Ross C G T.Delaunay triangulation of a random data set for is arithmic mapping［J］.The Cartographic Journal.1980，17:93 －99.

［3］张少丽，王毅刚，边浩.一种提高三角网格模型求交效率的算法［J］.计算机工程，2002，36(17):213 －215.

［4］张少丽，王毅刚，陈小雕.基于空间分解的三角网格模型求交方法［J］.计算机应用，2009，29(10):80－88.

［5］Tomas Moller.A fast triangle － triangle intersection test［J］.Journal of Graphics Tools，1997，2(2):25－30.

［6］Lee D T，Schacher.Two algorithms for constructinga Delaunaytriangulation［J］.International Journal of Computer and Information Sciences，1980，(9):219 －242.

［7］Johnstone J K，Sloan K R.Tensor product surfaces guided by minimal surface area Triangulations.In:Proceedings of IEEE Conference on Visualization，1995，354－361.

［8］Macedonio G and Pareschi MT.An algorithm for the triangulation of arbitrarily distributed points:applications to volume estimate and terrain fitting［J］.Computers＆ Geosciences，1991，17:859 －874.

［9］Brassel K E and Reif D.Procedure to generate thissen polygons［J］.Geographical Analysis.1979，11:289－303.

［10］Mc Cullagh M J and Ross C G T.Delaunay triangulation of a random data set for is arithmic mapping［J］.The Cartographic Journal.1980，17:93 －99.