晃动基座初始对准环境建模与仿真
梁禄扬 刘茜筠 杨 业
北京航天自动控制研究所,北京 100854
在地面风作用下,竖立在发射台上的火箭会产生晃动,这对火箭的初始对准性能产生不利影响[1]。因此,在火箭初始对准算法的研究中,通常需要模拟箭体在风扰动条件下的运动过程,并生成惯组测量输出数据,为初始对准仿真验证提供必要条件。对于初始对准用的惯组数据,工程上通常加入正弦或随机项模拟箭体晃动,但这种人为加入的运动并不能全面、真实地反应地面风的影响。因此,研究风扰动下初始对准环境建模与仿真方法具有重要意义。
本文研究了风扰动下火箭晃动环境的建模与仿真方法。该方法结合风场特性和振动理论,建立了地面风和箭体振动模型,并给出了捷联惯组测量输出的理想模型和误差模型。根据所建立的模型,比较了模拟风速谱与目标风速谱,对仿真获取的箭体振动特性与实测值进行了一致性分析,并验证了惯组理想条件下测量输出的正确性,最后结合惯组误差模型生成了测量输出数据,该数据可直接用于初始对准仿真验证。
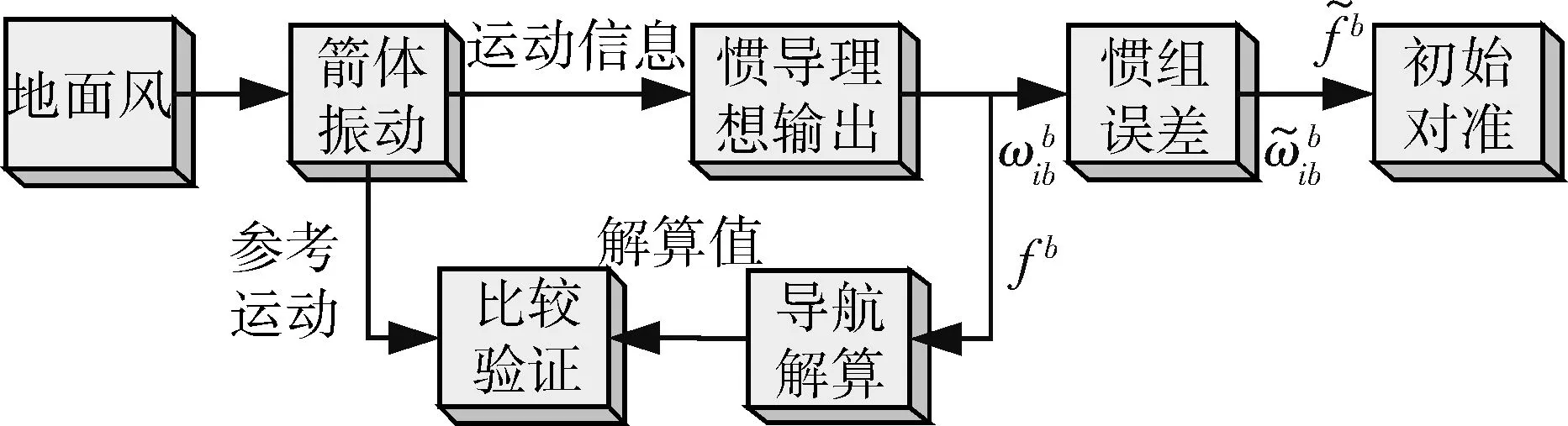
图1 晃动基座初始对准环境建模与仿真示意图
1 地面风建模
地面风一般指从地面至150m高度范围内的大气流动[1]。工程上将地面风分为定常风和脉动风。任意时刻的地面风v可认为是由定常风v1和脉动风v2两部分组成。定常风是指经过10min或更长一段时间测得的平均风。由于地表摩擦的作用,定常风沿地面向上大致呈指数函数分布,式(1)给出工程上风剖面随高度变化的指数模型。
(1)
其中,vref,v1分别为参考高度href(我国取10m)和高度h处的平均风速,z是地面粗糙度,p为粗糙度指数。
脉动风可看作平稳、各态历经的随机过程。加拿大的达文波特给出了脉动风速谱的经验公式:
(2)
式中,Sv(n)为风速谱密度,n是脉动风频率,k是地面粗糙度系数。
目前,模拟脉动风速主要使用谐波叠加法和回归方法。谐波叠加法计算量较大,而回归方法因其计算量小、速度快被广泛用于脉动风场模拟中[2]。本文将脉动风速建立为AR自回归模型(Auto Regressive Model):
(3)
其中,αi是回归系数,N(t)是均值为0、方差为1的随机过程。结合风速谱,采用Yule-Walker估计算法计算模型参数αi和σe[3-4],由AR模型得到脉动风速v2(t)。
利用模型(1)~(3)得到定常风和脉动风,二者相加即为地面风风速v。
2 箭体振动建模

(4)
引入广义坐标,采用振型分解法求解d(h,t):
(5)
φi(h),qi(t)分别是第i阶振型及其广义坐标,二者可根据式(6)和(7)分别求取。对火箭而言,可以只考虑第一阶振型的影响。
(6)

(7)

将φi(h)和qi(t)代入式(5),能解出高度h处的振动位移d(h,t)。若已知惯组安装高度hIMU,易得到惯组处的风振位移d(hIMU,t),将其分解至3个方向:
(8)
由于箭体风振位移相对于火箭高度l是小量[7],惯组处的姿态角可近似为:
(9)
将3个方向的振动位移和姿态角各自差分,可获得惯组位置处完整的三维线运动(位置、速度和加速度)和角运动信息(姿态角、姿态角速率)。
3 惯组测量输出模型
为模拟风扰动下的惯组测量输出数据,必须知道惯组安装处的三维运动信息。将振动模型获取的惯组运动信息作为已知条件,下面给出惯组理想输出模型和误差模型。
3.1 理想输出模型

(10)
(11)
(12)
(13)
其中,RM,RN为子午圈和卯酉圈半径。
4)b系相对于n系的转动角速度
(14)

比力方程改写为:
(15)

3.2 惯组误差模型
陀螺误差包含动态误差、静态误差和随机误差,具体的误差项与陀螺的种类、性质、工作环境等因素有关。本文以光学陀螺为例,其模型为
(16)
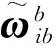
4 仿真分析
设水平方向的平均风速vref=10m/s,与箭体y轴夹角β=45°,惯组高度为46m,仿真3h。从图2看出,所模拟的脉动风速谱与达文波特谱基本吻合,风速在均值11.8m/s上下波动。由于惯组高度处的地面摩擦作用较小,风速均值略高于vref,同时脉动风具有零均值和随机分布特性,在风速中体现出一定的波动性。可见,风速的谱特性、波动性均符合实际,风速模拟方法是可靠的。

图2 风速谱比较和风速
自振频率和振幅是描述振动最基本的参数,因此,本文从这2方面对振动模型进行仿真分析。设火箭抗弯刚度1.53×1010Pa·m4,箭高58.34m,单位长度质量为8224kg/m,由模型计算出箭体一阶自振频率ω1=1.41rad/s,与火箭实测角频率1.26rad/s近似,这表明模型能正确体现箭体的频率特性,模型有效可信。图3描述了风载荷下的箭体振动位移变化情况。由于地面风的冲击作用,初始时刻的箭体振幅较大,30s后,振幅稳定在3.5cm内,最大幅值为3.44cm,接近实测的振幅4.42cm。由于影响振动的因素众多,本文仅考虑了最主要的地面风作用,可认为计算值与实测值一致。综上分析,自振频率和振幅与箭体实测值接近,模型能有效反映地面风作用下的箭体振动,这对模拟惯组输出是足够的。

图3 风载荷下的箭体振动位移
不考虑惯组和对准误差,采用双子样算法对3h的惯组理想输出进行导航(为避免发散,天向速度置0),得到位置、速度、姿态与参考值的最大误差如表1。显而易见,数据解算值与参考值误差很小,验证了惯组理想输出模型的正确性。

表1 IMU导航解算值与参考值的最大误差


图4 陀螺输出

图5 加速度计输出
5 结论
本文主要对风扰动下的环境进行了研究,提出了一种用于晃动基座初始对准的环境建模与仿真方法。该方法建立了地面风、箭体振动及惯组测量输出模型,并由模型仿真得到了风扰动下的惯组测量数据。仿真结果表明,箭体振动特性与实测一致,由惯组模型获得的测量数据与箭体晃动吻合,模型正确有效。因此,考虑惯组误差后的测量数据能真实反应外界扰动环境,可作为初始对准研究的仿真输入。该方法综合了地面风和箭体振动环境,能为晃动环境下初始对准仿真研究提供大量可靠的惯组模拟数据。
参 考 文 献
[1] 夏益霖.火箭在地面风作用下的振动载荷识别[J].强度与环境,1998,(4):1-7.(Xia Yilin.The Identification for Vibration Loads of Launch Vehicle in Ground-Winds [J].Structure & Environment Engineering, 1998,(4):1-7.)
[2] 张田,夏禾,郭薇薇.基于多维AR模型的桥梁随机风场模拟[J].中南大学学报(自然科学版),2012,43(3):1114-1115.(ZHANG Tian, XIA He, GUO Wei-wei.Simulation of Bridge Stochastic Wind Field Using Multi-variate Auto-Regressive Model [J].Journal of Central South University(Science and Technology), 2012,43(3):1114-1115.)
[3] 陈晓桐,卜国雄.某超高耸电视塔的脉动风载荷模拟及风振分析[J].科学技术与工程,2009, 9(1):48-51.(CHEN Xiao-tong, BU Guo-xiong.Simulation of Fluctuating Wind Load and Wind-induced Response Analysis of High-rise TV Tower [J].Science Technology and Engineering, 2009, 9(1):48-51.)
[4] 黄颖,房贞政.大跨度悬索桥随机风场的模拟研究[J].福州大学学报(自然科学版),2010, 38(6):878-879.(HUANG Ying, FANG Zhen-zheng. Research on the simulation of turbulent wind velocity of large-span suspended brideges[J]. Journal of Fuzhou University (Natural Science)[J].2010, 38(6):878-879.)
[5] 黄怀德,李宪姗,禇桂敏,等.振动工程(下)[M].北京:宇航出版社,1995.
[6] 杨茀康.结构动力学[M].北京:人民交通出版社,1987.
[7] 夏益霖,吴家驹.航天发射的低频振动环境及其模拟[J].强度与环境,1998(1):1-8.(Xia Yilin,Wu Jiaju.Low-Frequency Vibration Environment and Its Simulation for Aerospace Launch [J].Structure & Environment Engineering, 1998(1):1-8.)

