基于相位相关的图像匹配算法研究
胡 海,罗桂娥
(中南大学 信息科学与工程学院,湖南 长沙 410083)
图像匹配是评价两幅或多幅图像的相似性以确定同名点的过程。图像匹配算法就是设法建立两幅图像之间的对应关系,确定相应几何变换参数,对两幅图像中的一幅进行几何变换的方法。图像匹配是图像分析和处理过程中的基本问题。它在航空影像自动制图、图像三维重构、计算机视觉、遥感融合、模式识别、医学图像处理、影像分析等领域都有十分重要的应用。目前图像匹配算法分为基于图像特征和基于图像灰度两大类。在诸多现有的图像匹配算法中,基于相位相关的方法以其计算量小、抗噪声等优点得到广泛关注。
本文提出的基于相位相关的模板匹配方法不但有很高的匹配精度而且能精确地测量出相对图像对之间的相对平移量,但它对旋转变换很敏感。为了能够准确实现图像匹配,本文结合Fourier-Mellin变换求取图像的旋转量,并对图像进行匹配[1-5]。
1 Fourier变换位移理论
基于频域傅里叶变换相位相关法描述如下:
f1(x,y),f2(x,y)是定义在空间 R2的两幅图像,假定f1(x,y)是参考图像,图像 f2(x,y)是 f1(x,y)平移(x0,y0)后的观测图像,两者之间的关系可表示为:

根据傅里叶变换的性质有:
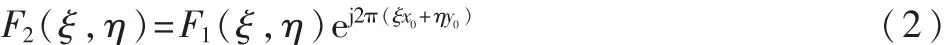
则两幅图像的互功率谱为:
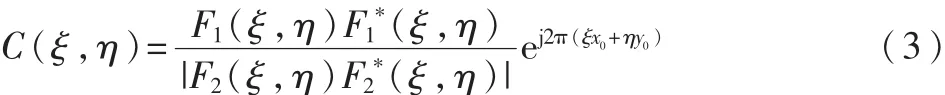

由该函数的中心位置可确定两幅图像之间的平移量。
2 Fourier-Mellin变换理论
匹配的两幅图像 s(x,y)和 r(x,y),其中 s(x,y)是r(x,y)经过平移、旋转和一致尺度缩放(即两个方向的尺度变换因子相等)变换后的图像,即:
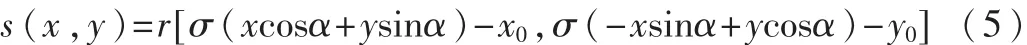
那么 s(x,y)和 r(x,y)对应 的 Fourier 变 换 S(u,v)和 R(u,v)之间满足:

其中,|·|表示频谱幅度。 从式(6)可看出,旋转角度 α 和缩放因子σ可以与平移量x0和y0进行分离计算。频谱幅度仅与旋转角α和缩放因子σ有关,而与平移量(x0,y0)无关,因此,可以通过图像幅度谱求出旋转角度α和缩放因子σ。令:

其中 rp和 sp分别是 r和 s在极坐标系 (θ,ρ) 中的幅度谱。那么很容易得出:

其中 λ=logρ,κ=logσ。
可以看出,通过上述变换,式(10)变换为与式(1)相同的形式,这样就可以在对数-极(Log-Polar)空间应用Fourier变换位移理论,按照式(1)~(4),求得 α 和 κ。
如果对数的底取为e,则

这样就求出了旋转角度α和比例因子σ。根据求出的 α 和 σ 对图像 s(x,y)进行反变换得到图像 s1(x,y),然后通过式(1)~(4)在图像空间计算出 s1(x,y)和 r(x,y)之间的平移量 x0和 y0。
式(11)被称为 Fourier-Mellin变换。
3 模板匹配理论
模板匹配是图像配准中最常用的方法,其基本思想是在观测图像中定义一个模板A之后,在参考图像中搜索与之匹配程度最高的模板B,然后根据这两个模板之间的平移关系确定出这两幅图像之间的配准参数。
本文采用式(12)来衡量模板 T(m,n)与所覆盖的子图 Si,j(i,j)的关系及两幅子图 Si,j(i,j)的相似性:
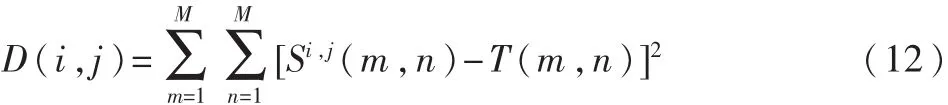
如果展开式(12),则有:
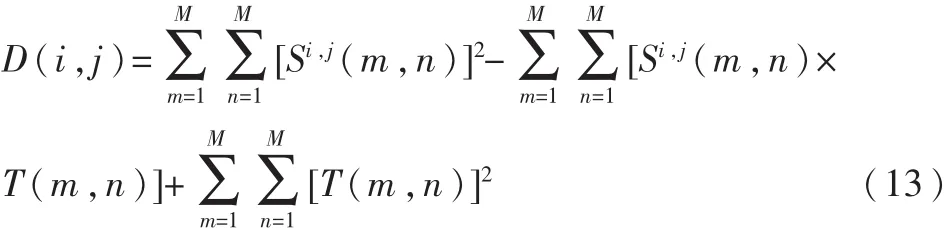
式(13)中第一项为子图的能量,第三项为模板的能量,都和模板匹配无关。第二项是模板和子图的互为相关,随(i,j)而改变。当模板和子图匹配时,该项有极大值。在将其归一化后,得到模板匹配的相关系数:
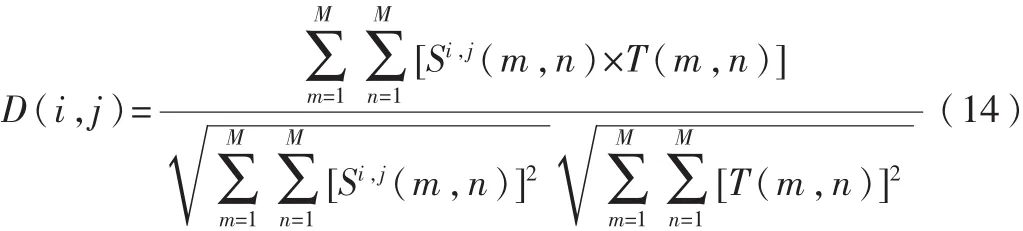
当模板和子图完全一样时,相关系数 R(i,j)=1。 在被搜索图S中完成全部搜索后,找出R的最大值Rmax(im,jm),其对应的子图 Sim,jm(i,j)即为匹配目标。
由于要遍历整幅图像,因此基于模板匹配的计算量很大,速度也慢。为解决此问题,本文采用的是基于相位相关的模板匹配方法。提供了两种方法:(1)通过在原始图像中选取模板,将模板(小图)与原始图像(大图)进行傅里叶卷积变换,从而进行模板匹配,即相位相关模板匹配;(2)在获取模板后,将模板(小图)扩充成与原始图像一样大小的大图,然后运用相位相关法,将模板(与原始图像一样大)与原始图像匹配对进行模板匹配,这是在第一种方法上的改进,即改进的相位相关模板匹配。
4 实验结果与分析
4.1 Fourier变换位移的验证与分析
首先选取原始图像,只对该图像进行人工平移,获得平移后的图像;然后通过Fourier变换位移的方法(即相位相关法),获取两幅图像的位移。图1中(a)和(b)采用的是 hat.bmp图像,位移预置值为(20,20)。

当然,如果是两幅图像,有一部分不同,通过Fourier变换位移的方法,也可以求取两幅图像的位移。图2中(a)和(b)采用的是 tu.bmp 图像,位移预置值为(0,256)。
实验结果如表1所示。通过该实验验证,相位相关法获取位移的效果很突出,准确率相当高,精确解的误差一般只有几个像素。需要注意的是,采用sobel、canny、robert等算法提取图像边缘信息时,将灰度图像转化为二值图像,虽然处理速度加快,但由于边缘检测算法的稳定性问题,可能会引起基于轮廓的相位相关算法失效。同时,只有位移变换的相位相关检测对旋转非常敏感,在基于Fourier-Mellin变换的图像匹配实验中会有所体现。

表1 Fourier变换位移结果
4.2 基于相位相关法的模板匹配实验
本文对三种模板匹配进行了实验。
(1)先通过原始图像选取模板,然后对模板和图像匹配对进行归一化相关模板匹配。
(2)在原始图像中选取模板,将模板(小图)与原始图像(大图)进行傅里叶卷积变换,从而进行模板匹配,即相位相关模板匹配。
(3)在获取模板后,将模板(小图)扩充成与原始图像一样大小的大图,然后运用相位相关法,将模板(与原始图像一样大小)与原始图像匹配对进行模板匹配,这是在方法(2)上的改进,即改进的相位相关模板匹配。
实验结果如表2所示。通过比较,可以看出:在匹配的精度上,三种方法都可以达到要求,但在匹配的速度上,改进的相位相关模板匹配明显要优于另外两种方法。归一化相关模板匹配和相位相关模板匹配采用的是小窗口(即模板)搜索方式,由于要遍历整幅图像,因此计算量很大速度也慢。而改进的相位相关模板匹配完全利用了相位相关法的优点,采用大窗口搜索方式,减小了计算量,从而提高了速度。
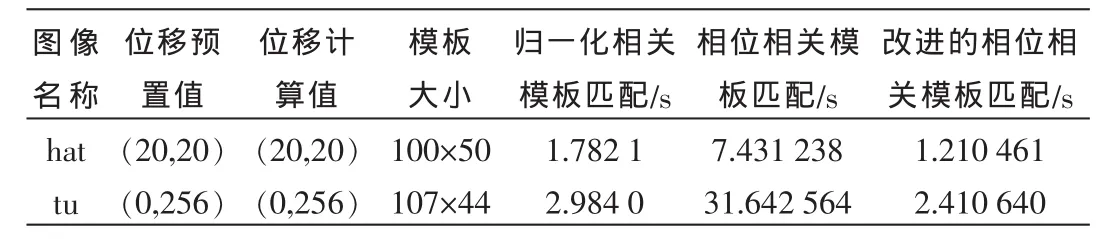
表2 三种模板匹配结果
4.3 基于Fourier-Mellin变换的图像匹配实验
为了求得图像的旋转量,本文结合Fourier-Mellin变换进行实验。图像匹配结果如表3所示。
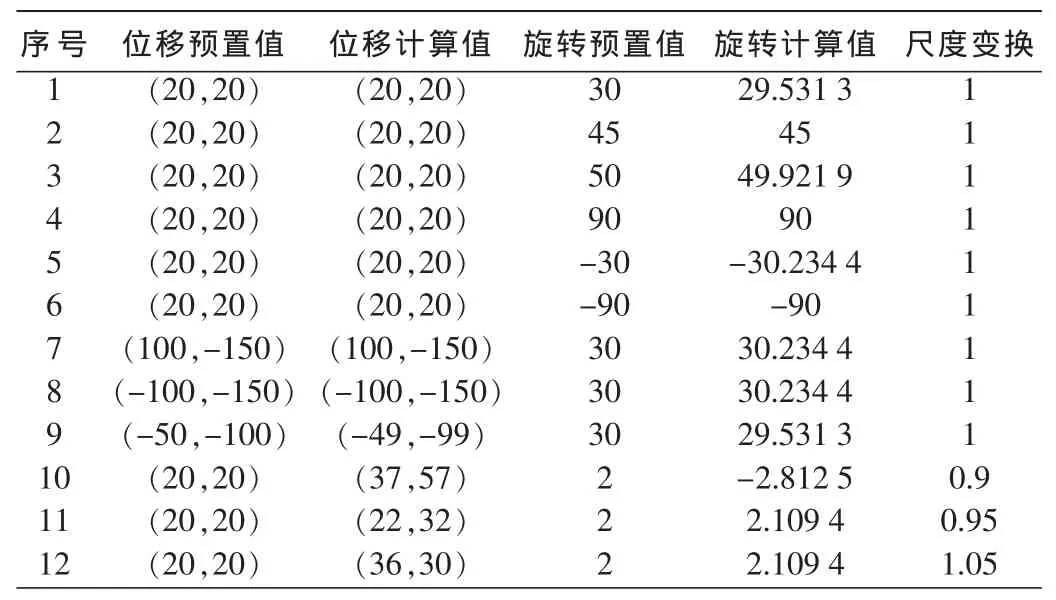
表3 Fourier-Mellin变换实验结果
图3给出了Fourier-Mellin变换实验部分结果,其中图3(a)为 hat.bmp原始图像,图3(b)为获取的头像部分,并在后续计算中进行(20,20)的位移变换,图3(c)为头像部分以图片中心旋转 30度,图3(d)为求取旋转量后将头像部分与原始图像进行的图像匹配,图3(e)和图3(f)为头像部分进行(100,-150)位移的图像及位移后的图像匹配,图3(g)和图3(h)为头像部分进行(-100,-150)位移的图像及位移后的图像匹配。实验时间最短的为2.204 9 s,最长为 2.694 4 s。

实验结果表明,结合Fourier-Mellin变换,图像匹配效果在精度上和时间上都比较好。Fourier-Mellin变换方法直接利用图像的整体频域特性,是一种基于非特征的图像配准方法,适用于有旋转变换的两幅图像之间的配准。要注意的是,图像需在尺度变换的允许值0.9~1.05的范围内,若超出范围,则匹配效果就比较差了。
本文提出一种基于相位相关算法的图像匹配方法。利用相位相关的计算量小、抗噪声等优点,将它应用于模板匹配,在图像匹配对平移的计算上可以得到很好的效果。为了解决图像的旋转问题,结合Fourier-Mellin变换,进行图像匹配。实验结果表明本方法在精度和速度上都能取得比较满意的效果。
[1] ZITOVA B,FLUSSER J.Image registration methods:asurvey[J].Image Vis.Comput.,2003,21:977-1000.
[2]BALCI M,FOROOSH H.Subpixel estimation of shifts directly in the Fourier domain[J].IEEE Transactions on Image Processing,2006,15(7): 123-124.
[3]李晓明,赵训坡,郑链,等.基于 Fourier-Mellin变换的图像配准方法及应用拓展[J].计算机学报,2006,29(3):466-472.
[4]李德广,李科杰,高丽丽.基于多尺度多方向相位匹配的立体视觉方法[J].仪器仪表学报,2004,25(4):600-602.
[5]方俊,伟翟超,金熠.相位相关法实现图像拼接的仿真与优化[J].计算机应用与软件,2008,25(1):207-208.

