分位数回归及其在R中的实现

何凤霞, 王凤竹



分位数回归及其在R中的实现

何凤霞*, 王凤竹

(华北电力大学 数理学院, 北京, 102206)

针对R中没有函数可以实现模型似然比检验、模型的拟合度等问题,编写了拟似然检验、拟合度的R代码, 运用实例给出分位数回归在R中实现的一般流程, 为以后分位数回归的算法研究提供了重要参考.

分位数回归; R; 拟似然比; 拟合度

经典回归与分位数回归的主要区别是: 经典回归描述自变量对因变量的条件均值影响, 而分位数回归描述自变量对于整个因变量的条件变化影响; 经典回归的随机项需来自均值为0且同方差的正态分布, 而分位数回归对于随机项不需具体分布的假设; 经典回归易受离群点的影响, 而分位数回归对于离群点不敏感等.

1978年, Koenker和Bassett[1]在最小绝对偏差估计理论的基础上首次提出了分位数回归的概念, 分位数回归在近20年广泛应用于经济、医学、生物等领域. 2006年, 李育安[2]介绍了分位数回归的概念及其应用; 荀鹏程等[3]将其应用于预测SARS的发病率.

目前，能实现分位数回归的软件主要有SAS、Eviews、Stata、R. R软件是一种开源、免费的优秀统计软件, 并且可以和全球一流统计专家讨论; 很多统计学的前沿方法均能实现, 其中quantreg包可以实现分位数回归.

本文主要介绍分位数回归(以线性为例)的概念、参数估计、参数检验以及模型的检验; 其次给出分位数回归参数估计、参数检验用R软件实现的函数, 对于R中没有函数可以实现模型似然比检验、模型的拟合度给出自编R代码; 最后以R自带数据为例, 给出一般分位数回归在R中实现的步骤.

1 分位数回归的简介

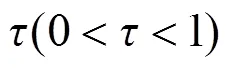
2 参数的估计

2.1 单纯形算法

单纯形算法[2]是由Koenker提出, 该算法适合样本量不大和自变量个数不多的变量, 当数据中存在大量离群点时, 单纯形算法估计出来的参数稳定性比较好, 但是在处理大量数据时运算的速度会显著降低[3]. R中实现函数为rq(formula, tau = 0.5, method = "br"), 其中formula表示公式对象; tau为分位点, 默认为中位数回归(即0.5分位数回归), 如建立自变量对因变量的0.9分位数回归, rq(formula, tau = 0.9); method表示估计参数的方法, 单纯形算法用"br"表示, 其实R中默认算法是单纯形算法, 一般样本容量不超过5 000、自变量个数不大于20, 经常用单纯形算法.

2.2 内点法

单纯形算法处理大样本时效率比较低, Barrodale、Koenker提出了内点法, 适合样本量较大, 且自变量个数少的样本数据[4]. 关于单纯形算法与内点法的比较, Koenker模拟数据[5]比较了自变量个数为= 4, 8, 16, 样本容量= 200, 400, 800, 1 200, 2 000, 4 000, 8 000, 12 000的情形; 得到当样本量比较少时, 单纯形算法优于内点法, 随着样本量的增加内点法优于单纯形算法. 在R中内点法的实现函数为rq (formula, tau, method = "fn").

除了单纯形算法和内点法在R中可以实现外, R也可以实现Portnoy、Koenker提出的预处理内点法等[4], 命令分别为rq(~, method = "pfn").

3 参数检验

本文主要介绍参数检验常用方法的3种: 误差为独立同分布、误差为非独立同分布、Bootstrap法.

3.1 误差为独立同分布

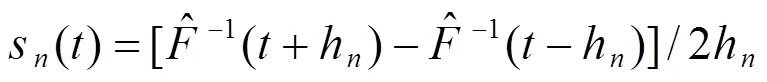
R中的命令为summary.rq(object, se = "iid", hs = T), 其中object是由上面命令rq返回的对象; se表示参数检验使用的方法; 当hs = T(默认)使用Hall-Sheater宽带, hs = F时, 使用Boginger宽带, 需要注意的是R中稀疏函数的估计使用RogerKoenker改进了差分方法.

3.2 误差为非独立同分布

对于误差为非独立同分布时, 参数的极限分布比较复杂, 如位移尺度假设模型:

3.3 Bootstrap法

Bootstrap法通过重新抽样来估计参数, 常用的方法有-Bootstrap、马尔可夫链边际Bootstrap.

3.3.1-成对Bootstrap

-Bootstrap是Bootstrap最一般的形式, 它首先对(,)进行重新抽样(抽取的样本数小于等于初始的样本数); 再计算分位数回归的系数估计值, 重复进行次抽样得到个系数估计值; 最后得到参数的渐近分布协方差. 在R中通过summary(object, se = "boot", bsmethod = "xy")实现.

3.32 马尔可夫链边际Bootstrap

He和Hu提出马尔可夫链边际Bootstrap[6], 它将多维线性规划问题转化为一维, 这些一维的解构成马尔可夫链, 简化运算. R中实现函数为summary(object, se = "boot", bsmethod = "mcmcb"). R中除了能实现上面2种方法外, 还可以实现Parzen和Wei and Ying提出的pwy法[7]等.

4 模型检验及拟合度

4.1 模型的检验

对于模型的检验, Koenker提出拟似然比(quasi-likelood-ration)[8]检验整个模型的显著性. 它假设所有参数均为0. 构造的统计量为:

4.2 模型的拟合度

分位数回归的拟合度[8]是Koerker、Machado提出的, 它的值介于0与1之间, 其表达式为:

5 实例

以R中quantreg包自带数据engel[9—11](这个数据是Roenker给出的, 它包含收入income、食物支出foodexp变量, 253个观察值)为例, 给出R中分位数回归的一般步骤.

第1步: 参数估计.

采用单纯形法求解参数估计tau = 0.5的回归系数. 命令:

>library(quantreg)#调用quantreg包

>data(engel)#读取engel数据

>attach(engel)#连接数据框的变量名到内存中, 以便直接调用变量

>fit=rq(foodexp~income, tau = 0.5, method = "br")#用单纯形法估计中位数回归的参数

>fit#查看回归估计参数

Coefficients:

Intercept income

81.482 0.560

结果解释: 中位数回归的常数项为81.482, 系数为0.56.

第2步: 参数的检验.

采用bootstrap的X-Y方法. R中的命令:

>summary(fit, se = "boot", bsmethod = "xy")

Value Std. Error t value Pr(> |t|)

Intercept 81.482 6.932 3.025 0.003

Income0.560 0.034 16.579 0.000

结果解释: 可以得到常数项的= 0.003 < 0.05, 系数的= 0.000 < 0.05, 所以在显著水平为0.05下参数均显著;

第3步: 模型的检验.

>source("C:/QLR.r")#调用QLR.r

>QLR(fit, hs = T, mod = F)

$tau

[1] 0.5

$QLR.statistic

[1] 437.4879

$p.value

[1] 0

结果解释: tau = 0.5的拟似然比统计量值为437.4879,值为0. 由于值小于0.05, 所以在显著水平0.05下显著.

第4步: 拟合度的计算.

>source("C:/R1.r")#调用R1.r

>R1(fit)#计算拟合度

$tau

[1] 0.5

$R1

[1] 0.620556

结果解释: tau = 0.5的拟合度分别为0.650 556.

第5步: 拟合图(图1).

图1 分位数回归的拟合图. 从上向下的直线依次是tau为0.1, 0.5, 0.9的拟合线.

>plot(income, foodexp, cex = 0.25, type = "n")

>points(income, foodexp, cex = 0.5, col = "blue")

>taus < -c(0.1, 0.5, 0.9)

>for (i in 1:length(taus)) {

>abline(rq(foodexp~income, tau = taus[i]),

lty = 1, col = "green") }

图2 回归估计值的变化图

第6步: 回归系数的图

>plot(summary(rq(foodexp~income, tau = 5:90/100), se = "boot", bsmethod = "xy"))

图2是tau = 0.05, 0.51, 0.52…, 0.9的回归估计值的变化图, 图2(a)是常数项变化图, 图2(b)是系数变化图. 水平实直线表示经典回归的估计值, 虚直线表示经典回归估计的95%置信区间的上下限; 灰色表示分位数回归95%置信带.

6 总结

相比经典的回归, 分位数回归可以描述自变量对于整个因变量的条件变化影响, 捕捉分布的尾部信息等特点. 近年来, 分位数回归广泛应用于金融、经济学、生物及环境等领域. 本文主要介绍分位数回归的思想、参数估计、参数检验、模型评价及其在R中的实现. 最后基于实例, 详细的给出R中实现的一般步骤.

附录1 拟似然比检验R代码

QLR=function(object, hs=hs, mod=T){

mt<- terms(object)

m <- model.frame(object)

y <- model.response(m)

x < - model.matrix(mt, m, contrasts = object$contrasts)

n < -length(y)

tau<- object$tau

coef<- coefficients(object)

method<-fit$method

p <- dim(x)[2]

rdf < -p - 1

res < -fit$residuals

fit0 < -rq(y ~ 1, method = method, tau = tau)

v1 < -fit$rho

v0 < -fit0$rho

if(mod){

sps < -as.numeric((summary(fit, se = "iid", cov = T, hs = hs))$scale)

sp < -1/sps

}

else{

sps < -as.numeric((summary(fit, se = "ker", cov = T))$scale)

sp < -1/sps

}

f<-2*(v0-v1)/(sp*tau*(1-tau))

Pvalue < -1-pchisq(f, rdf)

structure(list(tau=tau, QLR. Statistic = f, p. value = Pvalue))

}

程序的使用: object是rq返回的对象, hs的参数设置与误差为独立同分布中的hs一样. mod表示计算稀疏函数的方法, mod = T使用Koenker改进了差分的方法, mod = F使用的核函数法. 需要注意的是此时命令只能对应一个tau, 不能同时对应多个tau.

附录2 模型拟合度R代码

R1=function(object){

mt<- terms(object)

m <- model.frame(object)

y <- model.response(m)

tau <- object$tau

coef < - coefficients(object)

method < -fit$method

fit0 < -rq(y ~ 1, method = method, tau = tau)

v1 < -fit$rho

v0 < -fit0$rho

R1 < -1-v1/v0

structure(list(tau = tau, R1 = R1))

}

程序的使用: object是rq返回的对象.

[1] Koenker R, Bassett G. Regression quantiles[J]. Econometrica, 1978, 46(1): 33—50.

[2] 李育安. 分位数回归及应用简介[J]. 统计理论与方法, 2006, 21(3): 35—38.

[3] 荀鹏程, 顾坚, 顾海燕, 等. 中位数回归模型及自回归模型在北京市SARS发病预测中的应用[J]. 中国卫生统计, 2004, 4: 123—145.

[4] Barrodale I, Roberts F. Solution of anOverdeterminedSystemof Equationsin the l1Norm[J]. Communications of the ACM, 1974, 17(6), 319—320.

[5] 陈建宝, 丁军军. 分位数回归技术综述[J]. 统计与信息论坛, 2008, 23(3): 89—96.

[6] Portnoy S, Koenker R. The Gaussian Hare and the Laplacian Tortoise: Computability ofSquared-Error Versus Absolute-Error Estimators with Discusssion[J]. Statistical Science, 1997, 12(4): 279—300.

[7] Koenker R. Quantile Regression[M]. London: Cambridge U Press, 2005: 73—81, 202—204.

[8] He X, Hu F. Markov Chain Marginal Bootstrap[J]. Journal of the American Statistical Association, 2002, 97: 783—795.

[9] Parzen M I, Wei L, Ying Z. A resampling method based on pivotal estimating functions[J]. Biometrika, 1994, 81(2), 341—350.

[10] Roger Koenker, Jose A F. Machado. Goodness of Fit and Related Inference Processes for Quantile Regression[J]. Journal of the American Statistical Association, 1999, 94: 1296—1310.

[11] Koenker R, Bassett G. Robust Tests of Heteroscedasticity based on Regression Quantiles[J]. Econometrica, 1982, 50(1), 43—61.

Quantile regressionand itsrealizationin R

HE Feng-xia, WANG Feng-zhu

(School of Mathematics and physics, North China Electric Power University, Beijing 102206, China)

As there isn’t function realizing quasi-likelihood-ratio model test and goodness-of-fit in R, R-codes of quasi-likelihood-ratio and goodness-of-fit programmed are put forward. General process of quantile regression is developed based on an represent-ative example for providing important reference on quantile regression algorithm research.

quantile regression; R; quasi-likelihood-ratio; goodness-of-fit

10.3969/j.issn.1672-6146.2013.03.003

O 212.4

1672-6146(2013)03-0010-04

email: he_fx@126.com.

2013-07-06

(责任编校: 刘晓霞)