基于单道奇异值分解的微地震资料去噪方法

胡永泉，尹成，潘树林 （西南石油大学资源与环境学院，四川 成都610500）

巫芙蓉，李亚林 （中石油川庆钻探工程有限公司地球物理勘探公司，四川 成都610213）

刘玉海 （西南石油大学资源与环境学院，四川 成都610500）

众所周知，地震勘探中，提高地震资料信噪比和分辨率是一项贯穿始终的关键任务，而噪声是影响地震资料精度的重要因素之一。因此，地震资料处理的主要任务之一就是消除地震资料中的各种噪声，最大程度地提高地震资料的信噪比［1］。近年来，专家学者根据噪声和有效信号的特点提出了许多针对性的去噪技术，使得地震资料的信噪比得到较大程度的改善。奇异值分解 （SVD）技术就是其中一种有效的去噪方法［2］。

奇异值分解 （SVD）技术本质上是一种正交分解方法，它利用地震记录各道之间的相关性增强有效信号，压制不相关噪声，具有降噪效果明显、有效信号畸变较小的优点［3，4］。然而，对于倾斜或弯曲的同相轴，去噪效果不理想，这极大限制了该方法在实际生产中的应用［5～7］。鉴于此，不少专家学者对其进行了改进，陈遵德等［8］提出了基于倾角扫描叠加思想的SVD滤波方法，改善了SVD方法对倾斜或弯曲同相轴的去噪效果。钟本善等［9］提出通过将局部时窗内数据体进行旋转确保局部同相轴水平，再进行SVD去噪的同相轴自动追踪SVD去噪方法，充分发挥了SVD方法对水平同相轴去噪的优势。沈鸿雁等［10］提出在频域通过SVD提取奇异值进行信号频域重构，再进行反傅里叶变换进行波场去噪的频域SVD去噪方法，都取得了较好的效果。

以上各种改进方法大多要求地震资料具有一定的相关性和较高的信噪比，但对于微地震资料而言，噪声能量较强，有效信号淹没于噪声之中，有效信号没有明显可追踪的同相轴，致使上述方法失效。鉴于此，针对单道微地震资料周期性较强特点，笔者提出一种单道SVD去噪方法。该方法首先采用一定的时间延迟量利用单道微地震记录创建分解矩阵，使分解矩阵各维具有较强的相关性 （周期噪声），然后对矩阵进行奇异值分解，选取中间部分的奇异值对矩阵进行重构，最后通过奇异值分解反变换得到去噪后的单道记录，从而达到去除周期噪声和随机噪声的目的。将该方法应用于理论模型数据和实际微地震资料，都取得了较好的效果。

1 方法原理

1．1 SVD去噪原理

SVD去噪是利用地震记录的相关性，通过矩阵分解与变换，把矩阵旋转到一个新的坐标，然后利用信号与噪声的能量可分性，选取合理的奇异值，对地震数据进行重构，从而得到去噪后的记录11～13。利用SVD方法在去除噪声的同时，还可以保证信号的基本特征不变。

通常情况下，SVD去噪是基于地震剖面进行的。设地震剖面有M道，每道N个采样点，由地震剖面构成的矩阵用A表示，其元素为aji（其中，i为道号，j为时间样点号）即：

根据SVD理论，矩阵A的奇异值分解可表示为：

式中：k为奇异值序号；r为矩阵A的秩，奇异值个数与矩阵的秩相等；U是一个M×M的正交矩阵，由AAT的特征值向量构成；V是一个N×N的正交矩阵，由ATA的特征值向量构成；Σ是由AAT（或ATA）的奇异值σk按递减顺序组成的对角矩阵，即：

矩阵AAT（或ATA）的奇异值σk与特征值λk的关系为且满足σ1≥σ2≥ … ≥σr≥0。

式 （2）中的UkVkT是一个M×N的矩阵，称为矩阵A的第k个特征图像，在信号重构时，第k个特征图像的贡献与第k个奇异值成正比。由于奇异值是按照递减的顺序排列的，因此，对地震记录重构贡献最大的部分集中在最初的几个特征图像中［14］。可见，重构地震记录所需的特征图像的个数依赖于地震记录矩阵A各道之间的相关性，相关程度越高，重构时所需的特征图像个数就越少。若仅用m（m＜r）个特征图像来重构A，其重构误差ε为：

由此可见，原始地震记录具有一定的相关性是确保SVD取得较好效果的必要条件。在实际重构中，可根据具体需要选择不同奇异值实现记录的重构［15］。

1．2 单道SVD去噪原理

图1为四川某地区地面接收微地震资料剖面。从剖面可以看出，微地震记录噪声能量强，各道之间相关性较弱，没有明显可追踪的水平同相轴。采用常规SVD去噪方法很难去除噪声干扰。图2为单道微地震记录的部分数据，从图中可以看出，虽然单道微地震记录不是真正意义上的周期信号，但其体现出的周期性较强。倘若可以利用记录的周期性进行去噪处理，那么资料的信噪比将得到极大的改善。单道SVD去噪方法正是基于单道微地震记录噪声的周期性而提出的。单道SVD原理如图2所示。

单道SVD去噪方法主要利用单道微地震记录的周期性。方法首先根据一定的时间延迟量τ把单道的微地震记录分成彼此具有一定相关性的若干段 （各段之间数据可重叠），利用分段记录创建分解矩阵Dm，并对其进行奇异值分解；然后通过对奇异值分布规律的分析，选取有效信号对应的奇异值对Dm进行重构；最后通过SVD反变换得到去噪后的单道记录，从而达到去除噪声，突出有效信号，提高微地震资料信噪比的目的。

设单道地震记录采样点数为N，表示为x＝ ［x1，x2，x3，…，xn］，由此构成的分解矩阵Dm可表示为：

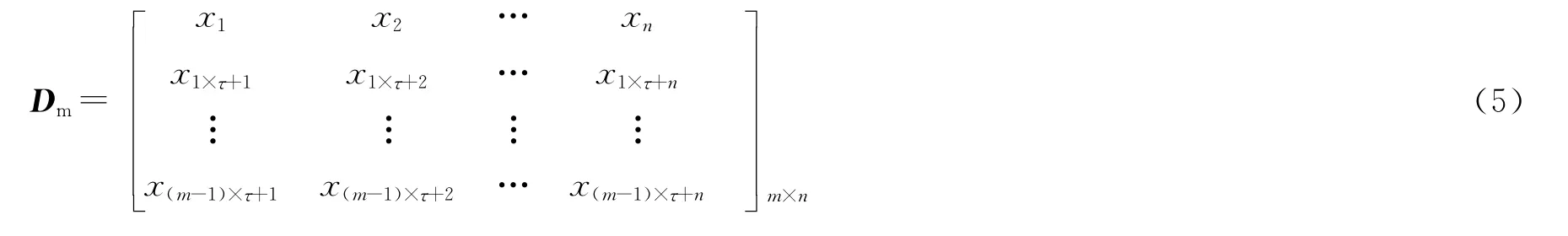
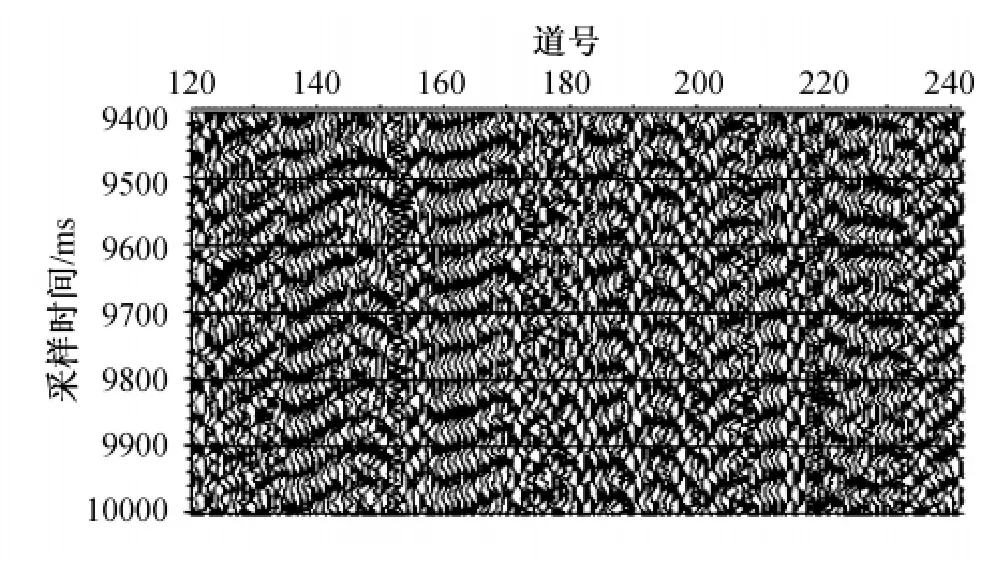
图1 四川某地区地面接收微地震资料剖面

图2 单道SVD原理图

式中：m为矩阵重构的维数；τ为时间延迟量；n为每维记录个数。各变量之间的关系可由下式确定：

对分解矩阵Dm进行奇异值分解，其奇异值由3部分组成，可由下式表示：

式中：SDM是分解矩阵Dm对应的奇异值；SW是强干扰对应的奇异值；SD为有效信号对应的奇异值；SN为随机干扰对应的奇异值。

分解矩阵Dm分解过后，3部分奇异值对矩阵重构的贡献是不同的。SW主要重构相关性较好的信号；SD主要贡献微地震有效信号；SN对重构矩阵各阶的贡献基本相同，主要对应随机噪声。因此，采取保留微地震信号对应的奇异值SD，把其他奇异值SW和SN置零的方式对矩阵进行重构，再经过SVD反变换便可以得到去除大部分周期噪声和随机噪声的单道记录。

单道SVD去噪的关键在于分解矩阵Dm创建时各个参数的选择，尤其是时间延迟量τ的选择。这是由于τ不但决定了Dm各维记录之间的相关性，而且还间接限定了分解矩阵Dm其他参数的取值，从而直接影响了方法执行效率与剖面重构的效果。针对单道微地震记录的特点，笔者对于时间延迟量τ的计算采用单道微地震记录自相关法归一化方法求取，可表示为：

式中：N为单道微地震记录的采样点数；l为单边自相关序列元素的序号，最大值与采样点数相等；p代表单道微地震记录元素的序号，最大值与采样点数相等；rl为单道微地震记录的单边自相关序列；rl′为归一化的单边自相关序列。时间延迟量τ等于使rl′＜0．5时的最小的l值。

由于单道SVD方法是通过选取有效信号对应的奇异值（中间部分奇异值）实现矩阵重构的，因此，要保证方法的有效性，就要保证奇异值个数不能过少。否则，很难从极少个奇异值中选取有效信号所对应的奇异值，从而影响重构效果。鉴于此，笔者对Dm维数m和每维记录数n的选择采取m＝n的取值方式。通过式（6）变换可得：

2 模型与实际资料处理

2．1 模型试验

图3（a）为含有较强周期性规律噪声的模拟地震记录，其中两条同相轴分别在200ms与400～700ms之间。图3（b）为剖面中单道加较强周期性噪声的时间序列。从图3（b）可以看出，即使噪声并非真正意义上的周期噪声，但具有较强的周期规律。为验证单道SVD方法的有效性，下面采用单道SVD方法对模拟地震记录进行滤波处理。

图3 模拟地震记录剖面及单道模拟记录噪声

图4 是经单道SVD滤波后采用不同奇异值进行资料重构的剖面。其中，构建分解矩阵Dm所需的时间延迟量τ通过自相关归一化法求取，分解矩阵重构时奇异值采用百分比的形式（奇异值序列），即奇异值序号占奇异值总数的百分比进行选取。

图4（a）是采用数值较大的奇异值进行重构的剖面，其结果主要对应单道记录中周期性规律较强的噪声；图4（e）和 （f）采用数值较小的奇异值进行重构的剖面，其结果主要对应单道记录中的随机干扰。不同之处在于，图4（e）中出现有效信号同相轴的影子，说明奇异值序号为奇异值总数46%的奇异值参与了有效信号的重构，因此可以将其定为参与剖面重构奇异值序列的上限。图4（b）～ （d）是采用奇异值序列中间部分不同范围奇异值进行重构的结果，可以看出，相对于图4（c），图4（b）有效信号能量较强，但信号周围干扰仍比较严重；图4（d）有效信号能量相对较弱。

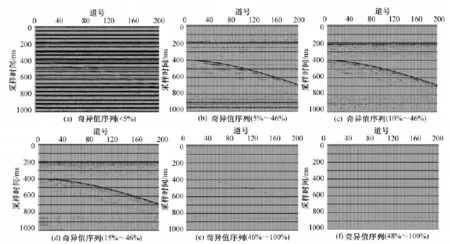
图4 单道SVD方法重构剖面

从上述分析可知，单道SVD去噪方法通常选取分解矩阵中间部分的奇异值进行矩阵重构，从而达到去除强周期性噪声和随机噪声，提高微地震资料信噪比的目的。通过实践表明，对于模型数据而言，参与剖面重构奇异值序号的下限应大于奇异值总数的5%，其上限应小于奇异值总数的46%。选取奇异值序列10%～46%范围内的奇异值进行重构可以得到较好的效果。

2．2 实际微地震资料处理

图5（a）是四川某地区微地震射孔资料的剖面图，图中椭圆内的信号为射孔资料直达波的初至同相轴，可以看出，微地震射孔资料的噪声能量较强，资料信噪比较低。图5（b）是射孔资料经常规SVD分解后奇异值分布曲线，可以看出，微地震资料经SVD分解后总共有200个奇异值，且奇异值总体呈现递减的趋势，变化较为平缓，这说明资料的整体的相关性不强，从图5（a）也可以得出相同结论，这就决定了传统SVD方法已不适用于微地震资料的去噪。

仔细观察原始剖面图5（a）中噪声特点可以发现，除随机干扰外，大多数地震道噪声的周期性较强，这就为单道SVD的应用提供了可能性。

图5 四川某地区微地震射孔资料剖面及奇异值分布

由于单道SVD是以单道微地震记录为基础，考虑到每道微地震资料的特点不同，这就导致每道微地震记录构成的分解矩阵与SVD分解后奇异值的分布规律存在差异。因此，实际应用中对于资料重构的奇异值采用百分比的形式 （即占奇异值总数的百分比）进行选取。其次，由于单道微地震记录的噪声并非完全意义上的周期噪声，因此，对于构建分解矩阵时时间延迟量τ的选取不能采用自相关方法，笔者采用自相关法归一化方法 （式 （8））进行求取，τ确定之后，通过式 （9）来确定分解矩阵的维数和每维数据个数。下面对单道微地震记录重构效果进行分析。

图6是采用单道SVD处理后的重构剖面。其中，图6（a）是采用数值较大奇异值进行重构的剖面，主要对应单道记录内周期性较强的噪声。这是由于在单道微地震记录的分解矩阵中，周期性较强信号的相关性较强，经SVD分解后，其主要对应数值较大奇异值的缘故。图6（b）和 （c）是采用较小奇异值进行重构的剖面，主要表现为随机噪声。这是由于在单道微地震记录的分解矩阵中，随机噪声的相关性较弱，对应SVD分解后数值较小奇异值的缘故。仔细观察图6（b）和 （c）可以看出，从图6（c）中可以隐约观察到直达波信号的影子，而图6（b）中却没有，这就说明了占奇异值总数35%～40%范围内的奇异值参与了直达波信号的重构。因此可以将重构所需奇异值序号的上限定在奇异值总数的35%。

图6（d）～ （f）分别采用不同范围中间部分奇异值进行重构的剖面，其目的在于消除单道微地震资料中周期性较强噪声与随机噪声的影响，达到突出有效信号的目的。其中，图6（d）是采用5%～35%范围内奇异值进行重构的剖面，相对于原始剖面图5（a），该方法对单道记录中周期性较强的噪声进行了较好的压制，对随机噪声也有不同程度的削弱。但就整体来看，剖面的信噪比并没有得到明显的改善。相对于图6（d），图6（e）和 （f）的去噪效果比较明显，直达波信号得到了较好的突出，资料的信噪比得到了较大程度的改善。

从上述分析可知，对微地震资料而言，参与剖面重构奇异值序号的下限应大于奇异值总数的5%，其上限应小于奇异值总数的35%。通常情况下，选取奇异值序列10%～35%范围内的奇异值进行重构可以得到较好的效果。

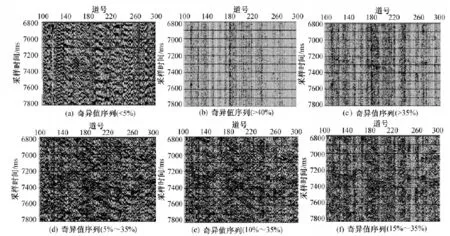
图6 单道SVD方法重构微地震射孔资料剖面

3 结 语

在对微地震资料特点和SVD去噪原理认识的基础上，提出了基于单道SVD的去噪方法。利用单道SVD分别对模型数据和实际微地震资料进行处理，从结果可以看出，基于单道的SVD可以去除大部分周期噪声和随机噪声，使有效信号更加突出，是一种适合微地震资料去噪的有效方法。与此同时，针对微地震资料的特点，通过实践给出了分解矩阵构建时各个参数选择的依据，以及矩阵重构时奇异值选取的合理范围，从而确保重构后的剖面具有较高的信噪比，为微地震的识别与震源定位提供有力的前提保证。

［1］陆文凯，李衍达．SVD分解提高地震资料的信噪比和分辨率 ［J］．石油地球物理勘探，1998，33（1）：145～149．

［2］Freire S L M，Ulrych T J．Application of singular value decomposition to vertical seismic profiling ［J］ ．Geophysics，1988，53 （6）：778～785．

［3］Maia B，Mirko B．Local singular value decomposition for signal enhancement of seismic data ［J］ ．Geophysics，2007，72 （2）：59～65．

［4］Liu Xuewei．Ground roll suppression using the Karhunen－Loeve transform ［J］ ．Geophysics，1999，64 （2）：564～566．

［5］苑益军，徐林 ．叠前线性干扰自动追踪SVD压制方法 ［J］．现代地质，2007，21（4）：733～737．

［6］陆文凯，牟永光 ．一种改进的SVD滤波器 ［J］．石油地球物理勘探，1996，31（5）：736～741．

［7］刘志鹏，赵伟，陈小宏，等 ．局部频率域SVD压制随机噪声方法 ［J］．石油地球物理勘探，2012，47（2）：202～206．

［8］陈遵德，段天友，朱广生．SVD滤波方法的改进与应用 ［J］．石油地球物理勘探，1994，29（6）：783～792．

［9］钟本善，何昌礼，杨忠民 ．复杂构造地区的SVD去噪技术 ［J］．成都理工学院学报，2000，27（1）：93～95．

［10］沈鸿雁，李庆春 ．频域奇异值分解 （SVD）地震波场去噪 ［J］．石油地球物理勘探，2010，25（1）：185～189．

［11］谢凤兰，赵改善 ．利用SVD法重建地震剖面 ［J］．石油物探，1990，29（4）：33～40．

［12］高静怀，朱光明，王玉贵 ．奇异值分解在VSP中的应用 ［J］．西安地质学院学报，1992，14（3）：71～78．

［13］詹毅，赵波 ．自动追踪SVD压制线性干扰方法的改进 ［J］．石油地球物理勘探，2008，43（2）：158～160．

［14］赵犁丰，姚玉玲．SVD方法在信号重构中的应用 ［J］．青岛海洋大学学报，1999，29（1）：101～106．

［15］裴江云，刘洪，李幼铭 ．在随机噪声背景下地震反射信号的增强 ［J］．地球物理学进展，2002，17（1）：91～95．