一种运动可靠的车辆主动悬挂线性控制器
钟小品,徐 刚
深圳大学机电与控制工程学院,深圳 518060
一种运动可靠的车辆主动悬挂线性控制器
钟小品,徐 刚
深圳大学机电与控制工程学院,深圳 518060
考虑车辆悬挂的触底和碰顶失效模式,设计一种运动可靠的车辆线性振动控制器,通过失效概率约束建立新的最优悬挂控制器问题,提出一个混合优化算法求解该最优线性控制器的反馈增益.结果表明,提出的控制器能以很小的性能代价换取较高的运动可靠性,使车辆悬挂控制器达到可靠性要求.
车辆主动悬挂;线性控制系统;悬挂碰顶;可靠性分析;运动可靠性;遗传算法
悬挂系统对乘员舒适性和车辆操纵性有重大影响,开发优秀的汽车悬挂系统越来越受到业内人士的重视[1-5].理想的悬挂能自适应车速和路况等变化以使轮胎尽量贴合路面,并使车身在起伏路面行进时尽量减少振动.传统的车辆普遍采用不依赖于外界能量的被动悬挂系统,这种系统被动且有限地吸收能量,因此对提升车辆的操纵性与乘员舒适性能力有限.不同于传统的被动悬挂,主动悬挂主动使用合适的作用力,改善车辆性能.自20世纪50年代主动悬挂的概念被提出以来,学者与工程师们研制了多种实用的主动和半主动悬挂系统,如2008年的Audi TT系列采用的Audi Magnetic Ride主动悬挂系统,以及同年Alfa Romeo Mito概念车采用的主动后悬挂系统.
主动悬挂设计的关键在于寻找一个可以同时兼顾车辆可操纵性和乘坐舒适性的控制律,不同的控制理论和方法[6-9]丰富了主动悬挂控制器的设计.由于车辆可操纵性和乘坐舒适性的综合性能指标通常表达为一个控制信号的2次型函数,因此,线性2 次最优调节器 (linear quadratic regulator,LQR)[9]仍然是最常用的简便方法之一.另则,当系统受到外界干扰时,例如路面输入、悬挂参数变化等噪声干扰,线性 2次高斯 (linear-quadratic-Gaussian,LQG)[9]随机最优控制可使该2次型性能指标达到最优.
尽管现有研究已提出许多基于LQG的悬挂控制器,但悬挂的可靠性仍未得到充分重视.随机噪声存在于悬挂系统的每一部分,由此引起的不确定性不但影响悬挂性能,且可能破坏系统.常见的悬挂控制器失效模式是悬挂触底和悬挂碰顶,即悬挂相对位移分别被压缩到最小和被拉伸至最大以致相关物理器件相互碰撞冲击而被损坏.随机运动引起的这种穿越安全区域失效模式称为首次穿越失效,失效率通过Rice穿越速率公式[10]推导得出.本研究以一个可靠性目标来约束该失效率,形成新的2次型悬挂性能指标优化问题,而传统的梯度优化方法已不再适应此问题,因此,结合梯度信息运用混合遗传算法以提高求解效率.结果表明,提出的运动可靠控制器保证了车辆主动悬挂的安全运行,即以很小的性能代价换取足够大的运行可靠性.
1 运动可靠的主动悬挂线性控制器
本文控制器的研究对象是车辆四分之一悬挂模型,如图1.其中,ms和mu分别为车体等簧载质量和轮胎等非簧载质量;ks、ku、cs和cu分别表示悬挂弹簧系数、轮胎弹簧系数、悬挂阻尼系数以及轮胎阻尼系数.Xs(t)、Xu(t)和Xg(t)分别表示车体的垂直位移、轮胎形变量和路面输入的随机过程.主动悬挂控制的目标即寻找最优主动控制力过程U(t).


图1 车辆四分之一悬挂模型Fig.1 A quarter car suspension model
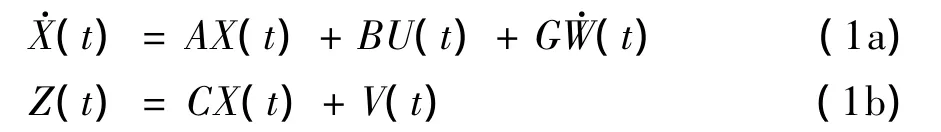
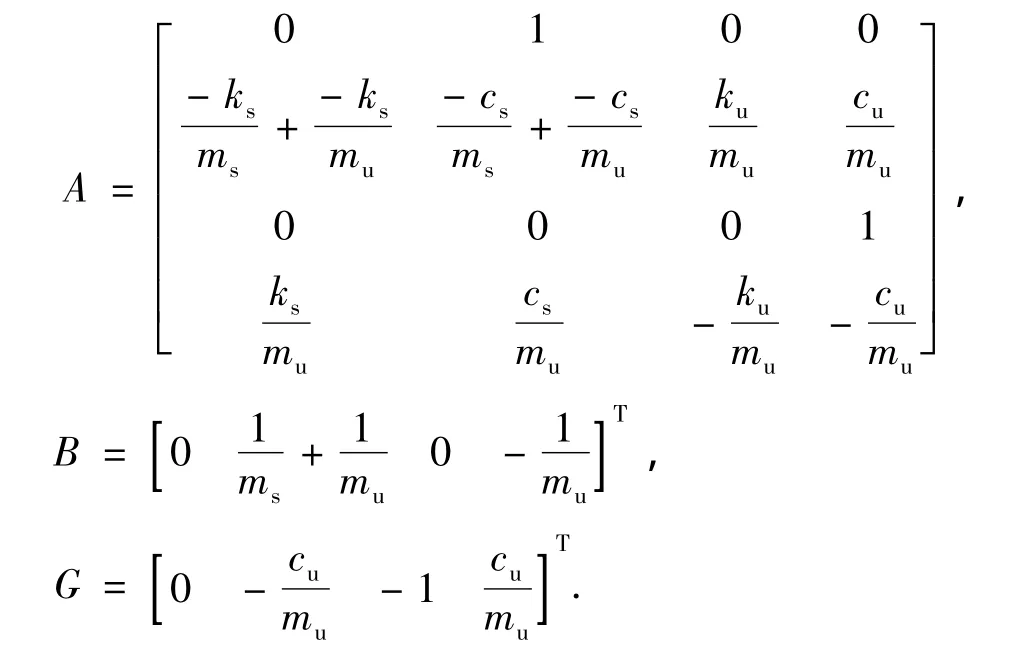
1.1 LQG控制器
悬挂的目标是提供乘员最大舒适性和车辆最优操作性,即寻找主动控制输入U(t)使得下列的2次性能指标函数最小,

其中,E{·}为均值函数,而半正定矩阵Q和正定矩阵R分别为状态变量和控制输入的权系数矩阵.因为实现简易性,线性控制被广泛应用,其控制律为

其中,K为反馈增益;t时刻状态变量X(t)可由特定的估计器输入,如卡尔曼滤波等.凭矩阵变换



主动悬挂的目标缩减为寻找一个反馈增益K*使得悬挂性能指标最小.其中,和K的关系可由Lyapunov方程决定,
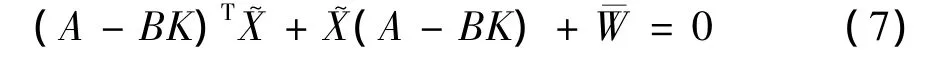
其中,P是Riccati方程的解.
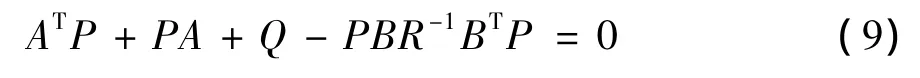
1.2 运动可靠性
运行过程中悬挂系统可能发生由随机振动引起的触底和碰顶现象,如图2.悬挂相对位移Xsu的安全区域为S={Xsu|b2≤Xsu≤b1},一旦离开安全区域,系统视为失效,即首次穿越失效[11].不失一般性,本研究仅考虑碰顶现象.显然累计至某时刻T的失效概率可被定义为



图2 悬挂触底失效和碰顶失效Fig.2 Suspension topping failure and bottoming failure
另一方面,在时间(0,T]内穿越边界的总次数n(T)服从泊松分布,

其中,风险函数υc(t)为系统在时刻t穿越边界b1的速率.对于首次穿越失效,失效概率即n(T)>0的概率,因此

穿越速率υc(t)由Rice公式[10]给出,



把式(16)代入式(13)以及可靠性要求(11)中,本研究提出一个新的线性控制律的优化问题,即寻找使得悬挂性能指标最优的反馈增益,且满足悬挂运动可靠性指标,

1.3 反馈增益优化
新问题(17a)~(17c)是多峰优化问题,可应用基于随机搜索的现代优化方法求解,例如,遗传算法.然而目标函数(17a)在全局最优处周围变得非常平坦,此区域无法保证随机搜索的高效收敛.受Bos[12]工作的启发,本研究使用一种混合优化算法,即在遗传算法中为每一代新群体中的个体进行一次梯度寻优.用式(17c)中的非线性不等式约束构造惩罚项可得无约束问题,

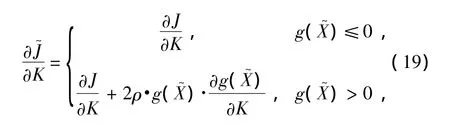


其中,罚因子ρ是足够大的常量.该代价函数1阶可导,且其中,⊗表示 Kronecker积运算[14].而对Lyapunov求偏微分可得

其中,I4是4×4单位矩阵.
至此遗传算法的个体可以通过上述微分过程寻优.可以证明,若初始增益K0使得A-BK0构成的控制器是稳定,则梯度寻优过程得到的增益也使控制器稳定[13].因此在遗传算法中每一代群体只需进行一次稳定性检测即可排除不稳定个体.具体计算过程参照表1所示的伪代码.

表1 反馈增益的混合优化算法Table 1 Hybrid optimizing algorithm for feedback gain
2 仿真分析
本研究仿真中,取路面输入为滤波后的白噪声过程,通过Hedrick提出简便状态空间法[15]容易确定由路面粗糙度[16]和行车速度决定的悬挂输入噪声水平W—.一般地车辆在运行过程中有两个经常变化的参数:由车身和乘客决定的簧上质量,以及输入噪声水平.为了测试不同环境下的悬挂性能,本文取两种1/4车身质量:重(ms=360 kg),轻(ms=240 kg);以及两种路面输入的噪声水平:高(W—=0.5×10-3),低(W—=0.3×10-4).其余悬挂参数见表2.为方便仿真Q被定义为4×4单位矩阵I4,而R=10-6,R足够小意味着用于作动器的控制力可以足够大.另一方面悬挂系统的动态失效模式为悬挂相对位移超过阈值b1=70 mm,在两小时即T=7 200 s内动态可靠性目标β=0.98.
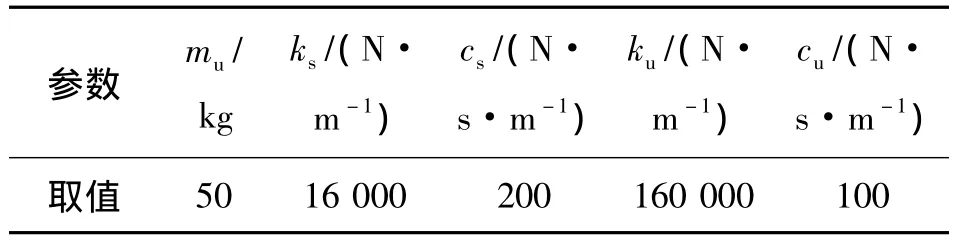
表2 四分之一悬挂系统的参数Table 2 Parameters of the quarter car suspension model
因此有4种不同的参数组合构成4个悬挂模型:重质量高噪声M(1)、重质量低噪声M(2)、轻质量高噪声M(3)以及轻质量低噪声M(4).总共需要4个对应的线性控制器以适应不同的运行环境,分别按不同参数求解问题(17a)可得4个不同反馈增益的控制器如表3.
不难发现在无约束情况下,模型M(1)和M(3)的运动可靠性都远小于可靠性目标0.98.而运动可靠性约束使得系统运动可靠性大于目标0.98,同时带来一定的性能损失,这些损失都小于10%,仍在可接受范围.另一方面,在模型M(2)和M(4)中,可靠性约束后最优增益变化不大,这是因为在低噪声水平下悬挂相对位移离开安全区域的概率接近于零,无约束最优增益已满足运动可靠性要求,其中,约束解与无约束解存在微小的不同是由遗传算法随机产生种群个体引起的.因此,除了簧上质量,噪声水平也是重要的参数,即路面粗糙系数和行车速度对运动可靠性影响很大.
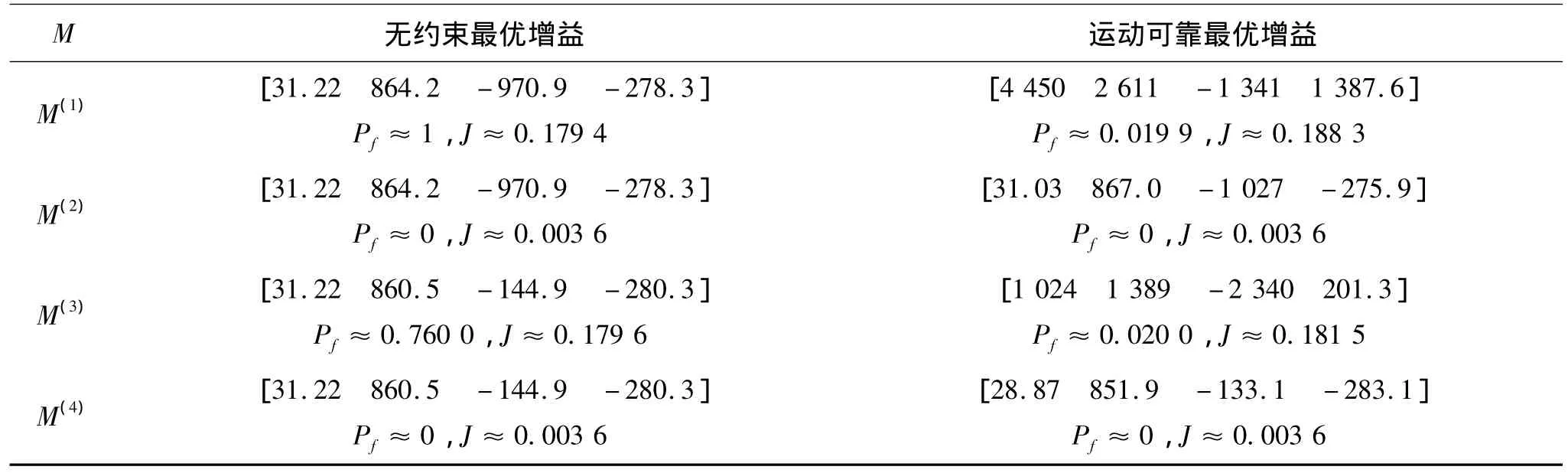
表3 无约束最优反馈增益与运动可靠最优反馈增益对比 (Pf表示失效概率,J表示悬挂性能指标值)Table 3 Optimal feedback gain comparison with constraint and without,Pfis failure probability and J denotes the performance index of suspension
使用阶跃路面偏移Xg输入,分别测试上述4个模型对于该输入的响应,可得如图3的结果,其中,黑色虚线和蓝色点划线分别表示被动悬挂和LQG控制器结果,而紫虚线和红实线分别表示β=0.97和β=0.98情况下使用运动可靠控制器的仿真结果.不难发现主动悬挂总是优于被动悬挂,而模型M(1)和M(3)运动可靠悬挂收敛速度稍微慢于LQG控制,如图3(a)和图3(c),但振幅较小,说明穿越安全边界的可能性较小,这种情况在可靠性目标越大的控制器中越明显.另一方面在模型M(2)和M(4)的仿真结果中,低噪声水平下运动可靠悬挂结果等同于LQG悬挂,因此响应重合,见图3(b)和图3(d).可见本研究提出的运动可靠性约束可以很小的性能代价换取较高的运动可靠性.

图3 四个悬挂模型控制器对阶跃路面偏移的响应Fig.3 Step responses of four suspension controllers
结 语
车辆主动悬挂的研究对提升车辆操控性及其乘坐舒适性具有重大意义,而LQG控制器被广泛应用于悬挂主动控制中,但悬挂的可靠性问题才刚开始引起学者们的注意.本研究考虑悬挂由随机运动带来的触底或碰顶运动失效模式,在LQG控制器的基础上提出一种基于运动可靠约束的主动悬挂线性控制器.其本质是在运动可靠性约束的线性2次控制问题中寻找最优反馈增益.由于求解新问题的复杂性,研究采用一种混合优化算法,即为结合梯度搜索的遗传算法.仿真结果表明,提出的线性控制器能以很小的性能代价换取较高的运动可靠性.该方法还可被应用于其他领域,如建筑物振动控制等.
/References:
[1]Poussot-Vassal C,Sename O,Dugard L,et al.A new semi-active suspension control strategy through LPV technique [J].Control Engineering Practice,2008,16(12):1519-1534.
[2]Cao J,Liu H,Li P,et al.State of the art in vehicle active suspension adaptive control systems based on intelligent methodologies[J].IEEE Transactions on Intelligent Transportation Systems,2008,9(3):392-405.
[3]Liu Xiandong,Pan Guojian,Shan Yingchun.Suspension parameters optimization based on neural network with road roughness input[J].Automotive Engineering,2006,28(6):561-564.(in Chinese)
刘献栋,潘国建,单颖春.考虑路面不平度神经网络的悬架参数优化 [J].汽车工程,2006,28(6):561-564.
[4]Lin J,Lian R J.Intelligent control of active suspension systems[J]. IEEE Transactions on Industrial Electronics,2011,58(2):618-628.
[5]Alleyne A,Hedrick J K.Nonlinear adaptive control of active suspensions[J].IEEE Transactions on Control Systems Technology,2002,3(1):94-101.
[6]Guo Shanglai.Stochastic Control[M].Beijing:Tsinghua University Press,1999.(in Chinese).
郭尚来.随机控制 [M].北京:清华大学出版社,1999.
[7]Li Shiyong.Fuzzy Control,Neural Control and Intelligent Control[M].Harbin:Harbin Institute of Technology Press,1998.(in Chinese).
李士勇.模糊控制,神经控制和智能控制论[M].哈尔滨:哈尔滨工业大学出版社,1998.
[8]Türkay S,Hüseyin A.A study of random vibration characteristics of the quarter-car model[J].Journal of Sound and Vibration,2005,282(1):111-124.
[9]Anderson B D O,Moore J B.Optimal Control:Linear Quadratic Methods[M].New York(USA):Prentice-Hall,1990.
[10]Rice S O.Mathematical analysis of random noise [J].Bell System Technical Journal,1945,45:46-156.
[11]Roberts J B.First-passage time for randomly excited nonlinear oscillators[J].Journal of Sound and vibration,1986,109(1):33-50.
[12] Bos A H W.Aircraft conceptual design by genetic/gradient-guided optimization[J].Engineering Applications of Artificial Intelligence,1998,11(3):377-382.
[13]Kurtaran B,Sidar M.Optimal instantaneous output-feedback controllers for linear stochastic systems[J].International Journal of Control,1974,19(4):797-816.
[14]Petersen K B,Pedersen M S.The Matrix Cookbook[M].Lyngby(Denmark):Technical University of Denmark,2006.
[15] Hedrick J,Firouztash H.The covariance propagation equation including time-delayed inputs[J]. IEEE Transactions on Automatic Control,1974,19(5):587-589.
[16]Gillespie T D,Sayers M.Measuring road roughness and its effects on user cost and comfort[Z].American Society for Testing and Materials,Philadelphia,Pa.,1985.
2012-03-28;Revised:2013-01-20;
2013-02-24
A dynamic-reliable linear controller for active vehicle suspensions
Zhong Xiaopin and Xu Gang†
College of Mechatronics and Control Engineering,Shenzhen University,Shenzhen 518060,P.R.China
In this research we consider the suspension failure modes of bottoming topping and develop a dynamicreliable design of linear vibration controller,i.e.we construct a new optimal suspension controller problem by imposing a constraint of failure probability.A hybrid optimization algorithm is further proposed to solve the feedback gains.Simulation results demonstrate that the proposed controller can trade a little performance for greater dynamic-reliability to satisfy the reliability requirement of vehicle suspensions.
active vehicle suspension;linear control system;suspension topping;reliability analysis;dynamicreliability;genetic algorithms
U 463.33;TP 273.1
A
10.3724/SP.J.1249.2013.02173
Foundation:National Natural Science Foundation of China(61203184);Natural Science Foundation of Guangdong Province(S2012040007116)
†
Professor Xu Gang.E-mail:xugang@szu.edu.cn
:Zhong Xiaopin,Xu Gang.A dynamic-reliable linear controller for active vehicle suspensions[J].Journal of Shenzhen University Science and Engineering,2013,30(2):173-178.(in Chinese)
国家自然科学基金资助项目 (61203184);广东省自然科学基金资助项目 (S2012040007116)
钟小品 (1979-),男 (汉族),广东省河源市人,深圳大学讲师、博士.E-mail:xzhong@szu.edu.cn
引 文:钟小品,徐 刚.一种运动可靠的车辆主动悬挂线性控制器[J].深圳大学学报理工版,2013,30(2):173-178.
【中文责编:方 圆;英文责编:卫 栋】

