基于多通道图像相关性的改进GRAPPA算法

周山雪，谢国喜

1)深圳职业技术学院电子与通信工程学院，深圳 518055;2)中国科学院深圳先进技术研究院生物医学与健康工程研究所劳特伯医学成像中心，深圳 518055

基于多通道图像相关性的改进GRAPPA算法

周山雪1，2，谢国喜2

1)深圳职业技术学院电子与通信工程学院，深圳 518055;2)中国科学院深圳先进技术研究院生物医学与健康工程研究所劳特伯医学成像中心，深圳 518055

针对传统GRAPPA(generalized auto-calibrating partially parallel acquisitions)算法存在随欠采样倍数增加重建图像质量下降的问题，提出一种改进算法.该算法利用多通道图像间的更多相关信息对传统GRAPPA算法进行改进，突破传统GRAPPA算法仅利用自校准信号进行权重系数估计的局限，并进一步使用已采集数据之间的一般相关性.实验结果表明，改进后的GRAPPA算法能重建出更高质量的磁共振图像.

磁共振成像;并行成像;GRAPPA;相关性成像;加速成像;图像重建

磁共振成像(magnetic resonance imaging，MRI)技术［1］因具有无辐射伤害、可任意方位扫描、对软组织敏感度高.可同时获得检查部位的形态信息和功能信息，自20世纪80年代至今，在医疗诊断领域得到长足发展.与其他成像技术比较，MRI技术具有很大的优越性和应用潜力［2］.然而，由于受到奈奎斯特采样定理和自身成像机制的限制，其成像速度较慢，且成像质量易受呼吸和血流等运动因素的影响而出现伪影，限制了MRI技术的进一步应用.因此，如何缩短成像时间，改善成像质量是MRI技术关注的问题.

Sodickson［3］和 Pruessmann 等［4］分别提出并行成像算法SMASH(simultaneous acquisition of spatial harmomcs)和SENSE(sensitivity encoding)，实现了磁共振降采样成像.并行成像算法使用多个射频接收线圈同时接收来自不同位置的多个感应信号，并利用线圈的空间敏感度信息实现磁共振降采样成像，使得每个线圈采样的数据量大大减少，从而缩短了成像时间［5］.Griswold 等［6］在 VD(variable density)-auto-SMASH［7］基础上，进一步提出GRAPPA(generalized auto-calibrating partially parallel acquisitions)算法，现已成为MRI领域中广泛应用的并行成像算法之一.该算法在对K空间数据进行欠采样基础上，利用K空间的平移不变性原理，将对自校准信号进行拟合得到的权重系数应用到K空间的其他欠采样区域，由此拟合得到完整的K空间数据，对该K空间数据进行逆傅立叶变换即可重建出完整图像.由于GRAPPA算法能够用于任何结构的相控线圈阵列［8］，在低降采样因子 (2～3倍)的情况下也能保证较好的图像质量，因此得到广泛应用.然而，此方法实际上仅利用已采集数据间部分的相关信息，所以在欠采样倍数较高时 (4倍及以上)难以获得高质量的重建图像.为此，本研究将相关性重建模型［9］引入GRAPPA算法中，利用各通道线圈采集数据之间的相关性，进行相关函数估计，再通过相关函数估计权重.因此，所利用已采集数据间的相关信息大大增加，在高倍欠采样时，也能重建出更高质量的图像，并给出相应的实验验证.

1 重建理论

1.1 GRAPPA重建算法

GRAPPA重建算法是一种基于K空间的并行图像重建技术，其假设K空间具有线性平移不变性，即K空间的任一数据点可以通过其邻近数据点的线性拟合得到.邻近数据点与被拟合数据点的相对位置决定了各邻近数据点贡献的权重大小.该算法在采集数据过程中，除欠采样数据外，还需额外采集位于K空间中心位置的自校准数据 (auto-calibration signal lines)，称之为ACS线，也就是中心位置以奈奎斯特频率进行的全采样，其采样轨迹如图1.

图1 GRAPPA算法的采样轨迹Fig.1 Sampling trajectory of GRAPPA algorithm

图1仅绘出1个线圈K空间的采样轨迹 (为简单起见，只在相位编码方向上做欠采样处理)，kx和ky分别代表频率编码和相位编码方向.R为欠采样因子 (或称加速因子).

传统GRAPPA算法 (以multicolumn multiline interpolation，MCMLI［10］为例)重建图像的过程可以概括为:

1)用采集到的欠采样数据和ACS线数据进行权重系数估计，拟合的数学公式为式(1)左边代表直接采集到第j个线圈的ACS线数据，右边部分代表要拟合出的ACS线处的数据.其中，Sl(ky+nRΔky，kx+mΔkx)为第l个线圈的欠采样数据;Δky和Δkx分别为相位编码和频率编码的间隔;by和bx分别为重建所需的相位编码方向和频率编码方向块的个数;coils为相控阵列线圈的总数;Wj，k(l，n，m)为要计算的权重系数.

2)利用求得的线圈权重系数 Wj，k(l，n，m)和采集到的欠采样数据拟合出每个线圈的其他未采集到的数据，拟合公式同式(1).只是式(1)左边的(ky+kΔky，kx)变为要拟合的其他位置未采集到的数据 Sj(ky+kΔky，kx).

3)将上述拟合出的未采集到的数据、欠采样得到的数据以及ACS线数据合并，恢复出每个线圈完整的K空间数据，并将其进行逆傅里叶变换，即可得每个线圈的重建图像.利用平方和 (sum of square)公式就可得到最终重建图像.

传统GRAPPA算法的关键在于利用自校准ACS数据拟合出权重系数，将此权重系数平移运用到其他欠采样位置，从而得到未采集到的数据点.此方法存在以下缺陷:① 仅利用自校准ACS数据拟合出权重系数，当采集的自校准数据ACS线较少时，拟合得到的权重系数误差较大，从而影响图像重建质量.理论上，ACS线越多，重建图像的质量越好.但若ACS线太多，则失去了并行成像加快K空间数据采集的意义;②传统GRAPPA算法假设的权重系数为线性平移关系，而已有研究表明这实际上只是一种非线性关系的近似［11］，当仅利用这种线性平移关系进行数据拟合时会造成信息的丢失.此外，块 (kernel)的选取并未包括全部的欠采样数据也会影响重建的精度.

1.2 基于多通道图像相关性的改进GRAPPA算法

2012年Li等［9］提出基于图像相关信息的并行重建模型.该模型引入数学上相关函数的一般概念，使图像重建过程尽可能多的利用已采集到数据间的相关性.因此，其在加速倍数较大的情况下也能得到较好的图像重建质量.但是，该方法需要扫描全采样的K空间数据进行相关函数和权重系数的计算，无法实现单幅欠采样图像重建，限制了该方法的实际应用.本研究针对传统GRAPPA方法和现有相关性并行成像模型的优缺点，提出一种基于多通道线圈图像相关性的改进GRAPPA算法.该算法将基于相关信息的并行重建模型的基本思想引入GRAPPA算法中，将GRAPPA算法中丢失的数据相关信息尽量找回，以期充分利用所有的采集数据.其可以进一步提高GRAPPA算法的图像重建质量，具体模型如图2.

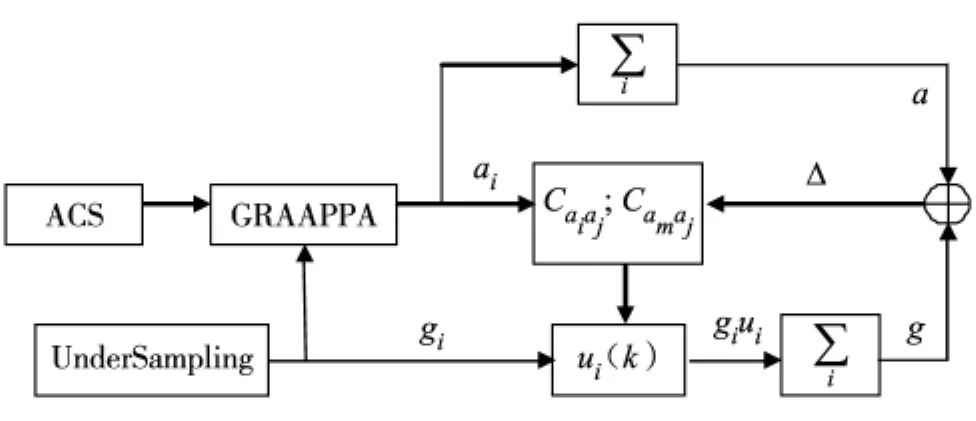
图2 基于相关性改进的GRAPPA算法模型Fig.2 Improved model of GRAPPA algorithm based on Correlation

在本算法中，利用1套多通道实际采集的全采样K空间数据，提取ACS线和欠采样数据gi来模拟实际的ACS线和欠采样K空间数据.该算法重建图像的过程可概括为:

1)利用GRAPPA重建算法得到每个通道完整的K空间数据ai(k)，并由实际全采样的K空间数据通过欠采样轨迹函数 ti(k)，得到欠采样数据gi(k)(i=1，2，…，coils).

2)由相关函数的定义估计各相关函数的初值Caiaj和Camaj，其计算公式为

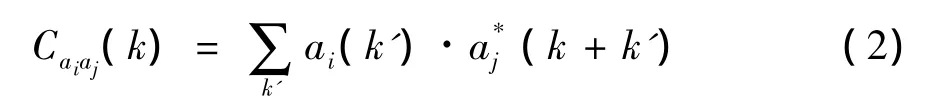
其中，k'和k为相应的K空间坐标;ai(k)和aj(k)分别为第i、j线圈相应的K空间数据;*为复数共轭.

3)由相关函数Caiaj(k)的初值估计权重系数ui(k)，利用最小二乘法得到一组线性方程进行估算

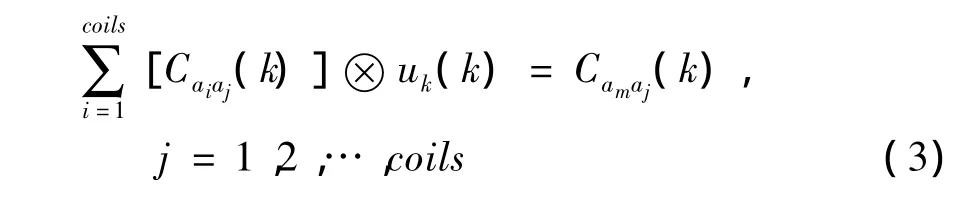
其中，am(k)为需要重建的第m个通道实际采集的K空间数据 (图2中用GRAPPA恢复的每个通道的K空间数据);ui(k)为要求得的权重系数.

4)利用求出的权重系数ui(k)与实际采集的K空间欠采样数据(图2中用一套欠采样数据gi模拟)共同拟合恢复出全部K空间数据(图2中giui，i=1，2，…，coils).

5)利用恢复出的K空间数据更新相关函数和权重系数，回到2)～4)步.循环重复上述步骤直到得到满意的图像数据g输出为止.这也就是所谓的迭代求权和重建图像的过程.输出图像一般为通过重建的每个通道的K空间数据giui经过逆傅里叶变换后得到的平方和像.

2 仿真实验与结果分析

2.1 材料与方法

本算法借用1套标准的脑部图像数据进行实验.这套数据是1组脑部横截面2维图像数据，在GE的3T系统 (GE Healthcre Waukesha，WI)上，用8通道的头线圈通过T1加权的2D自旋回波序列采集得到的.采集参数设置为重复时间TR=700 ms，回波时间TE=11 ms，矩阵大小为256×256，视野为22 cm×22 cm，层数为10.欠采样K空间数据通过对全采样K空间数据手动设置加速因子R获得.将相位编码方向上相应的加速因子R值设为零，保留K空间中心 (24或32条)数据作为自校准数据 (ACS线).

实验中将所有线圈全采样数据的平方和图像作为参考图像，并比较本算法和标准GRAPPA算法重建的图像.采用均方根误差 RMSE(root mean square errors)值定量评价重建图像的质量.它反映了重建图像与参考图像的接近程度，RMSE值越小，表示重建精度越高，其计算公式为

其中，Irecon为重建图像数值;Iref为参考图像数值.

同时将本算法和标准GRAPPA算法重建的图像分别与参考图像的差值图像进行比较，这样会更加直观些.所有算法均使用Mathworks，Natick，MA公司Matlab7.0软件实现.

2.2 结果及分析

图3为上述1套脑部vivo数据的图像重建结果.上面一行为采用标准GRAPPA算法重建的图像，下面一行为用本算法重建的图像.其中，R分别为2和4，校正数据ACS线分别为24和32.

由图3可见，当R=2时，两种算法重建图像的质量都很好.无论是用较少的自校准数据 (ACS线为24)，还是用较多的自校准数据 (ACS线为32)，通过肉眼都看不出伪影和噪声.但当R增大到4时，标准的GRAPPA算法重建的图像，无论是在ACS线为24，还是32时，都有伪影 (图3白箭头所指位置)，且较少的自校准数据重建的图像噪声也比较大.而改进的GRAPPA算法在R=4时，当ACS线为24或32时，都有较好的重建图像质量.

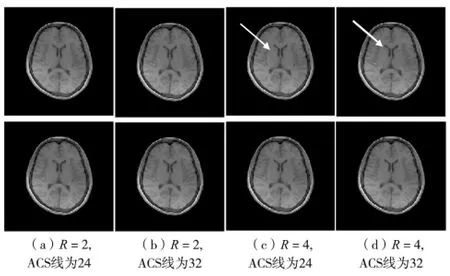
图3 GRAPPA算法和改进算法重建结果比较Fig.3 Reconstructions comparison of GRAPPA and improved algorithm

图4还给出了图3(c)和(d)的差值图像.其中，上一行为GRAPPA算法重建的图像和两者的差值图像，下一行为改进算法重建的图像，以及它与参考像的差值图像.选取R=4，校正数据ACS线分别为24和32.

显然，图4中改进算法与参考像的差值图像的轮廓没有GRAPPA重建像与参考像的差值图像的轮廓突出.说明改进算法的重建图像与参考图像的差别小了一些，即改进算法重建图像的质量好.为定量说明这一点，计算每幅图像的RMSE值，结果见表1.

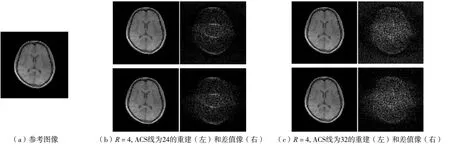
图4 GRAPPA算法和改进算法重建像与参考像的差值图像Fig.4 Difference image of GRAPPA algorithm and improved algorithm for reconstruction image

表1 标准GRAPPA和改进GRAPPA的RMSE值Table 1 RMSE values of standard GRAPPA and improved GRAPPA

由表1可见，①在同一加速因子R下，两种算法重建图像的RMSE值都随ACS线的增加而下降.这说明ACS线越多，重建图像的质量越好.因为ACS线越多，包含的原始信息就越多，计算出的权重系数也就越准确，但运算时间会有所增加;②两种算法随着欠采样因子R的增大，RMSE值也都会增大.说明重建图像的质量随着R的值增大而变差;③本算法的RMSE值总小于标准GRAPPA算法的RMSE值.说明本算法重建图像的质量要优于标准的GRAPPA算法.

但是，本算法适当增加了重建时间，而且单幅图像质量提高的效果还不是很多.这主要是因为单幅图像本身的数据量比较少.相关性的优越性尚未充分体现.在实际临床扫描中，一般都有多幅先前的图像数据可以参考.特别是在动态扫描过程中都要采集一系列的图像数据，它们具有极大的相关性.若将相关函数用统计的方法估算并不断更新，则后面的扫描中就可极大提高欠采样因子R，这样节约的时间要远多于本算法增加的时间，因此，这值得进一步向下研究.

结 语

本研究针对目前标准GRAPPA算法在高倍加速时，可利用的数据量过少，无法重建出较好质量图像的问题，将基于相关信息并行重建的基本思想引入GRAPPA算法中，建立相应理论模型，并通过实验证明提出的基于多通道图像相关性的改进GRAPPA算法的重建图像质量优于传统GRAPPA算法的，且在R=4时，使用较少的自校准数据ACS线就能重建出较好质量的图像.若ACS线适当增加，或有较多的先前数据可以利用，会使效果更加明显.在实际的临床扫描中，一般都具有多幅先前的图像数据可以利用，因此，本算法具有良好的应用前景.

/References:

［1］Lauterbur P C.Image formation by induced local interactions:examples employing nuclear magnetic resonance［J］.Nature，1973，242(8):190-191.

［2］Zhao Xiping.Magnetic Resonance Imaging［M］.Beijing:Science Press，2004.(in Chinese)

赵喜平.磁共振成像 ［M］.北京:科学出版社，2004.

［3］Sodickson D K，Manning W J.Simultaneous acquisition of spatial harmonics(SMASH):fast imaging with radiofrequency coil arrays［J］.Magnetic Resonance in Medicine，1997，38(4):591-603.

［4］Pruessmann K P，Markus W，Markus B S，et al.SENSE:sensitivity encoding for fast MRI［J］.Magnetic Resonance in Medicine，1999，42(5):952-962.

［5］Carlson J W.An algorithm for NMR imaging reconstruction based on multiple RF receiver coils［J］.Journal of Magnetic Resonance，1987，74(2):376-380.

［6］Griswold M A，Jakob P M，Heidemann R M，et al.Generalized autocalibrating partially parallel acquisitions(GRAPPA) ［J］.Magnetic Resonance in Medicine，2002，47(6):1202-1210.

［7］Heidemann R M，Griswold M A，Haase A ，et al.VDAUTO-SMASH image［J］.Magnetic Resonance in Medicine，2001，45(6):1066-1074.

［8］Chen Wufan.Parallel magnetic resonance imaging:past，present and future［J］.Chinese Journal of Biomedical Engineerin，2005，24(6):649-654.(in Chinese)

陈武凡.并行磁共振成像的回顾、现状与发展前景［J］.中国生物医学工程学报，2005，24(6):649-654.

［9］Li Y，Dumoulin C.Correlation imaging for multiscan MRI with parallel data acquistion ［J］.Magnetic Resonance in Medicine，2012，68(6):2005-2017.

［10］Wang Z，Wang J，Detre J A.Improved date reconstruction method for GRAPPA ［J］.Magnetic Resonance in Medicine，2005，54(3):738-742.

［11］Chang Y，Liang D，Ying L.Nonlinear GRAPPA:a kernel approach to parallel MRI reconstruction［J］.Magnetic Resonance in Medicine，2012，68(3):730-740.

2013-02-05;

2013-03-04

An improved GRAPPA algorithm based on the correlation between multi-coil images

Zhou Shanxue1，2†and Xie Guoxi2

1)School of Electronic and Communication Engineering，Shenzhen Polytechnic，Shenzhen 518055，P.R.China
2)Paul C.Lauterbur Reasearch Center for Biomedical Image，Institute of Biomedical and Health Engineering，Shenzhen Institues of Advanced Technology Chinese Academy of Sciences，Shenzhen 518055，P.R.China

Conventional GRAPPA(generalized auto-calibrating partially parallel acquisitions)algorithm uses the auto-calibration data of additional acquisition to fit the missing K-space data and reconstruct desired image from a multi-coil under-sampling data set.However，as the acceleration factor increases，reconstruction quality decreases quickly.To address this issue，we propose a new reconstruction algorithm to improve the conventional GRAPPA by taking more correlation information of multi-coil images.It overcomes the limit of conventional GRAPPA which only uses the auto-calibration data to estimate the fitting coefficients.It takes the available relationship of all the data making reconstructed the better-quality image.Experimental results show that the proposed method could provide a better reconstruction than conventional GRAPPA.

MRI;partially parallel imaging;GRAPPA;correlation imaging;accelerated image;image reconstruction

R 445.2;TN 911.73

A

10.3724/SP.J.1249.2013.02162

Foundation:National Natural Science Foundation of China(81000611)

†

Associate professor Zhou Shanxue.E-mail:zhoushanxue@szpt.edu.cn

:Zhou Shanxue，Xie Guoxi.An improved GRAPPA algorithm based on the correlation between multi-coil images ［J］.Journal of Shenzhen University Science and Engineering，2013，30(2):162-166.(in Chinese)

国家自然科学基金资助项目 (81000611);深圳市南山区科技局资助项目 (南科院2009012)

周山雪 (1962-)，男 (汉族)，湖南省常德市人，深圳职业技术学院副教授，湖南大学硕士生导师.E-mail:zhoushanxue@szpt.edu.cn

引 文:周山雪，谢国喜.一种基于多通道图像相关性的改进GRAPPA算法 ［J］.深圳大学学报理工版，2013，30(2):162-166.

【中文责编:方 圆;英文责编:卫 栋】