混凝土辐射供冷RC简化传热模型的改进及实验验证

田 喆，牛晓雷，胡振杰，王志强，尹兴蕾

(1. 天津大学环境科学与工程学院，天津 300072；2. 天津大学建筑设计研究院，天津300072；3. 中国市政工程华北设计研究总院，天津 300074)

混凝土辐射供冷系统中具有较大热容量的建筑体作为空调末端的一部分，直接参与向房间的供冷供热过程．建筑蓄热体的主动介入不但使空调末端内部冷(热)量传递过程趋于复杂，更改变了建筑内传热和空调系统供冷的耦合过程．混凝土辐射供冷的非稳态传热过程研究，对系统的运行和控制具有重要意义．混凝土辐射供冷的传热过程不仅包括混凝土内的三维非稳态传热，还包括管内流体沿管道方向及两相邻供水管之间的传热过程，同时混凝土楼板又具有较大的热容量，从而导致冷量传递过程趋于复杂并具有滞后性．目前，该传热过程多采用数值方法和传热简化模型模拟方法来计算，其中传热简化模型不仅计算量小，且计算精度较高，因而研究多集中于此．热阻热容(thermal resistance and capacity，RC)网络法和导热传递函数(conduction transfer function，CTF)法是其中两种代表性方法，已应用于商用软件 Trnsys和 Energy Plus中[1-3]．

RC法基于电路与建筑材料传热的相似性，利用电路计算方法，将时域下非稳态传热转化到频域计算，降低了模型的复杂程度和计算量，其难点在于管道节点与核心温度层节点之间的等效热容热阻的确定．与 RC模型相比，CTF法只能处理线性方程，计算管道与楼板传热时需假定流体静止且沿管长方向温度相同，因此不能很好地模拟变流量工况下混凝土辐射供冷末端的非稳态传热过程．

国内外许多学者对 RC法简化模型进行了研究．Weber等[4]提出了一种针对混凝土辐射供冷系统非稳态传热的RC模型，模型中热容热阻参数的确定需依靠数值模拟，计算过程复杂．本课题组在前期研究中，将核心温度层概念[5]引入混凝土星型 RC传热模型[4]，采用系统几何与热工参数确定 RC模型核心层热容、热阻的方法建立了混凝土 RC传热简化模型[6]，但未实现系统供冷量随供水温度或流量变化时的非稳态传热模拟．为此，笔者在 RC传热简化模型基础上进行优化研究，加入供水流量参数的模拟，构建了融合管道换热的混凝土辐射供冷楼板非稳态传热RC简化模型，实现了在供水温度和流量联合变化工况下对楼板动态热响应的模拟分析，并搭建实验台用实测数据验证模型的准确性和适用性．

1 辐射供冷楼板非稳态传热 RC简化模型的优化

在原混凝土 RC传热简化模型(见式(1))基础上，将有限元法与Schmidt[7]所用方法相结合，以模拟沿供水管方向对上下壁面的传热过程，计算得出管道内供水温度沿流动方向各点的变化．将管道供水温度的变化与混凝土 RC简化模型的二维平面传热模型相结合，继而改进了辐射供冷楼板非稳态传热 RC简化模型．

1.1 混凝土楼板供水温度传热矩阵的确立

在实际运行中，混凝土楼板内的供水温度会沿流动方向发生变化，由于混凝土楼板蓄热能力较大，本文忽略相邻管间传热，将混凝土楼板内供水盘管简化为直管段处理．设管道内z点处供水温度为3()tz˜，由能量守恒定律可得

同时由已建立的混凝土 RC传热简化模型式(1)，可得到管壁与外界换热量为

将供水温度随时间的变化以复数形式表示，再由

式(3)可得到管道末端供水温度为

1.2 混凝土楼板非稳态传热优化模型

得到管内任一点供水温度后，将3()tz˜带入式(1)，得到混凝土楼板内任一点处的传热模型为并可求得沿供水方向任一点的供水温度和热流密度.

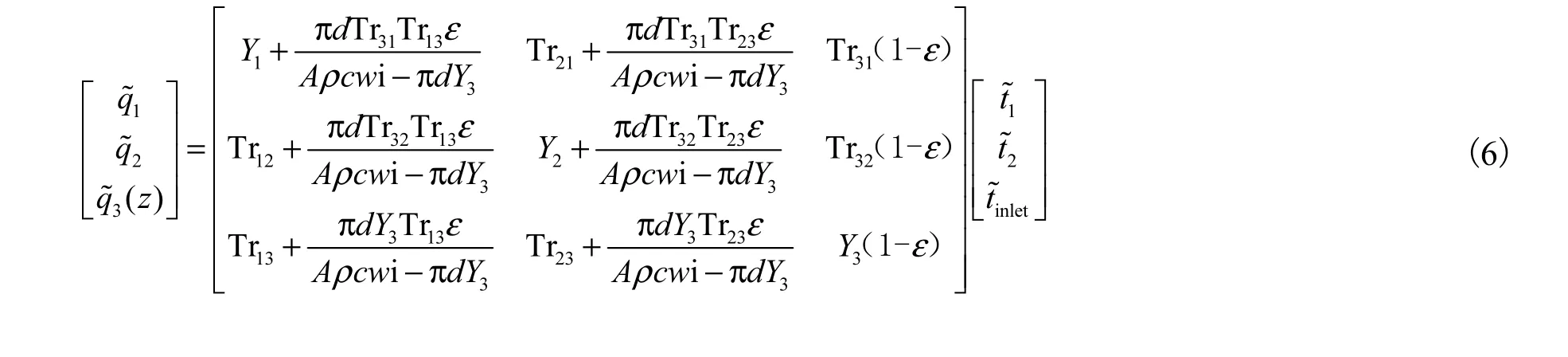
同时，为全面反映混凝土辐射供冷系统非稳态传热过程，可通过式(6)所得结果计算各核心层间温度变化情况．以楼板上层为例，设层间温度为 t11，t12，…，t1,N，则对含有热容节点的核心层温度 ta，tb，…，tn可由式(7)计算．

式(6)中的传递矩阵包含了楼板几何参数、混凝土物性参数、供水温度和供水流速，与原模型的主要区别在于第 3个温度节点边界条件的确定．改进模型中，3t˜为楼板起点供水温度，而非供回水温度的平均值，因此在楼板结构一定、供水温度和楼板上下表面温度已知的情况下，求解式(6)可得到工质流量和温度联合变化工况下通过楼板的热流密度变化情况，

2 混凝土楼板非稳态传热RC简化模型验证

2.1 全尺寸实验台搭建及测点布置

为验证式(7)模型的可靠性，笔者依据辐射供冷末端测试标准[8]，搭建了混凝土楼板辐射供冷系统的全尺寸测试舱体(见图 1)，测试不同工况下楼板的传热过程，将实验值与上述模型模拟值进行对比分析．测试舱内部尺寸为 4,m×2,m×3,m(长×宽×高)，围护结构为200,mm厚的聚氨酯夹板，并在拼接缝处用密封胶将缝隙密实．测试舱体具有良好的保温性和气密性，可用于辐射末端设备的热工性能测试、动态热响应实验及室内热环境测试．实验采用内热源形式模拟负荷．

图1 测试舱整体示意Fig.1 Overall scheme of test cabin

实验混凝土辐射供冷楼板采用 C15豆石混凝土制作，满铺于测试舱体地面，厚度为 100,mm，并在其下方铺设 20,mm厚聚苯板保温材料．供水管采用双回形布置，埋置于楼板表面下40,mm处，见图2．

图2 混凝土楼板的供水管布置Fig.2 Layout of the water supply pipe in concrete floor

制作实验楼板时，在楼板中心相邻供水管间不同厚度(楼板上表面、20,mm 深处、40,mm 深处、100,mm 深处、保温层下表面)的楼板结构内布置 T型热电偶，共25个温度测点，见图3．

图3 楼板内部温度测点分布Fig.3 Distribution of temperature measuring point inside the slab

实验通过测试两组非稳态工况(供水温度变化工况和供水流量变化工况)，测得混凝土楼板的稳态传热和动态热响应情况．将实测值与模型模拟值进行对比，验证模型的准确性．

2.2 模型输入参数及验证参数选取

优化后的混凝土楼板非稳态传热 RC简化模型(优化模型)采用MATLAB科学计算软件编写计算程序．模型的输入参数为：测试舱体尺寸、混凝土楼板的结构及物性参数、供水管物性参数、模型 3个节点的温度(楼板上、下表面空气温度、，供水温度)及流量边界参数．

混凝土楼板的热动态响应可通过楼板内部温度场的变化来反映，因此选择楼板表面热流密度及楼板内部垂直方向温度分布作为目标参数，进行模拟值和实测值的对比分析．其中表面热流密度可通过实测地板表面及其上方空气温度值由式(8)～式(10)计算求得[9]．

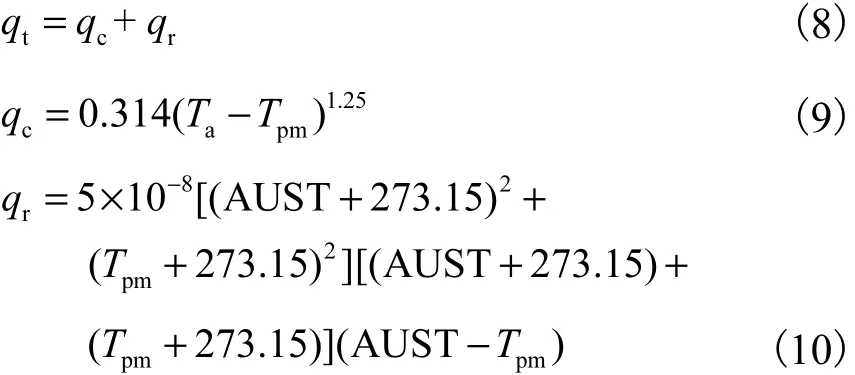
2.3 非稳态工况验证

非稳态工况下，混凝土楼板的蓄热过程伴随着传热过程，由于混凝土蓄热能力较强，其热动态响应十分复杂和缓慢．为此，本文采用改变供水温度和供水流量的非稳态工况验证模型，利用供水温度和流量的突变较为明显地反映出实测混凝土楼板的热动态响应过程．

2.3.1 供水温度变化工况

实验中，供水温度在0,h时刻由16,℃变化至18,℃.在非稳态过程中，模型的 3个节点温度随时间变化，因此本文将实验数据拟合成多项式函数作为模型输入参数．

模拟得到楼板表面热流密度和楼板内部温度随时间的变化曲线，并与实测值对比，如图 4所示；同时，采用可反映两组数据一致性的Bland-Altman法[10]对实验数据和模拟结果进行分析．

从图中可以较为直观地看出模型模拟值的变化趋势与实测值相近，热流密度模拟值整体略大于实测值，3个垂直方向温度比实测值略小，这是由于内部温度是由热流密度反算得出(见式(7))，热流密度与温差成正比，从而模拟值1q˜越大求得的内部温度越小(实测值变)．对比数据可知热流密度的模拟值与实测值的偏差较小，平均为5,W/m2；内部温度的模拟值与实测值最大偏差为 0.5,℃，在实际应用中可以接受，模型准确性较高．

图4 供水温度阶跃变化工况下各参数的动态响应及分析Fig.4 Dynamic response and analysis of the parameters under the condition of water supply temperature step change

值得注意的是，在热流密度下降前，模拟曲线存在一个向上的突起，这是由模型边界参数的傅里叶级数展开造成的(由于内部温度是由热流密度反算得出，模拟温度同样存在此反常现象)，在实际运行中并不存在，产生突起的原因需要在今后模型研究中进一步完善．

图4中4组125例配对数值的差值，最多有7.22%(9/125)的点在Bland-Altman法所规定的95%一致性界限以外(多为反常点)，模拟值与实测值偏差也较小，因此认为模拟和实验结果具有较好的一致性．

2.3.2 供水流量变化工况

实验时维持供水温度相对恒定(控制为(16±0.1),℃)，在8.5,h时刻供水流量由0.663,m³/h变化至0.418,m³/h，直至各项测试参数稳定．

将实验数据拟合成多项式函数作为模型输入参数．模拟得到楼板表面热流密度变化曲线与实测数据的对比见图5，并采用Bland-Altman法对实验数据和模拟结果进行分析．

图5 流量变化工况中各参数的动态响应及分析Fig.5 Dynamic response and analysis of the parameters under the conditions of flow change

由图5可知，供水流量变化引起的楼板内热流密度和温度的动态热响应不明显，但可看出模型模拟值的变化趋势与实测值相近．热流密度模拟值仍整体略大于实测值，最大差值不超过 5,W/m2．由于混凝土辐射供冷楼板自身的特点，流量变化后楼板回水温度变化不大，因此 3个垂直方向温度变化不大，模拟值与实测值最大偏差小于0.5,℃．图中4组141例配对数值的差值中，最多有4.26%(6/141)的点在Bland-Altman法所规定的 95%一致性界限以外，因此可认为模型对流量变化的模拟和实验结果具有较好的一致性．

通过上述对比验证可知，改进后的模型在模拟非稳态工况下楼板动态热响应时存在一定适用范围.由于原 RC简化模型采用傅里叶级数展开的方法将时域内边界条件的变化转化为频域形式，当边界条件变化时，在突变时刻前后有多个正弦分量的叠加，造成模拟值的振荡，使模拟误差加大，因此原 RC简化模型不适用于变化周期小于 2.51,h的连续非稳态过程模拟[5]．改进模型中同样采用上述方法处理边界条件，不适用于变化周期小于2.51,h的连续非稳态过程模拟．

3 结 语

基于混凝土辐射供冷系统星形 RC传热简化模型，将供水温度和流量等参数列入热流密度计算的传递矩阵中，使得原模型得以改进．实现了供水温度和流量联合变化工况下楼板动态热响应的模拟分析.实验验证结果表明，改进后的RC传热简化模型对于非连续性温度(流量)变化引起的混凝土楼板热动态响应模拟误差较小，具有较高的适用性，可为楼板热动态过程研究以及混凝土辐射供冷系统的运行调控提供理论分析的方法．

符号说明：

［1］ TRNSYS16. Transient System Simulation Program [R].USA：University of Wisconsin Madison，2006.

［2］ 晋欣桥，柴小峰，杜志敏. 过渡季节VAV空调系统送风温度的优化控制策略[J]. 天津大学学报，2009，42(5)：586-590.

Jin Xinqiao，Chai Xiaofeng，Du Zhimin. Optimal control strategy of supply air temperature for VAV air conditioning systems under transition season[J].Journal of Tianjin University，2009，42(5)：586-590(in Chinese).

［3］ EnergyPlus. The Reference to EnergyPlus Calculations[R]. California，USA，2010.

［4］ Weber T，Johannesson G. An optimized RC-network for thermally activated building components [J].Building and Environment，2005，40(1)：1-14.

［5］ Koschenz M，Dorer V. Interaction of an air system with concrete core conditioning [J].Energy and Buildings，1999，30(2)：139-145.

［6］ Liu Kuixing，Tian Zhe. Establishment and validation of modified star-type RC-network model for concrete core cooling slab[J].Energy and Buildings，2011，43(9)：2378-2384.

［7］ Schmidt D.Models for Coupled Heat and Mass Transfer Processes in Buildings：Applications to Achieve Lowexergy Room Conditioning[M]. Sweden：Division of Building Technology，KTH-Royal Institute of Technology Stockholm，2001.

［8］ EN14240 Ventilation for Buildings—Chilled Ceilings Testing and Rating [S]. European Standard：CEN，2004.

［9］ Jeong J W，Mumma S A. Practical cooling capacity estimation model for a suspended metal ceiling radiant cooling panel [J].Building and Environment，2007，42(9)：3176-3185.

［10］ Bland J M，Altman D G. Statistical methods for assessing agreement between two methods of clinical measurement[J].The Lancet，1986，327(8)：307-310.