异步脉冲无线电超宽带系统的渐近带宽

徐 娟，吴雨润，吕彬彬，周 静

（同济大学 电子与信息工程学院，上海 201804）

超宽带无线电是近年来发展迅猛的一种新型无线传输技术，它是基于冲激脉冲（皮秒级窄脉冲）自身的宽频谱特性，通过对具有特殊波形的冲激脉冲进行调制获得载有信息且符合频带要求的无线电信号，即所谓脉冲无线电超宽带（impulse radio ultrawide band，IR-UWB）［1］.使 用 跳 时 （time hopping，TH）码为每个发射脉冲引入一个可变时延，从而可以降低多用户干扰.

超宽带技术具有广阔的应用前景，可用于无线个域网、无线通用串行总线（universal serial bus，USB）等短距离高速数据传输及无线传感网和精确定位、智能交通系统等中长距离中低速数据传输等.尤其是跳时IR-UWB具有诸如宽频谱、低功耗、低成本和低系统复杂性、可与现存的窄带和宽带无线通信网络共存、类似噪声的信号、精确的定位能力和强抗多径衰落能力等独有的特性［2］，因此跳时IRUWB是无线传感网物理层的首选方案.

跳时IR-UWB多用户系统中由于存在多用户干扰，因此对多用户系统差错概率的研究非常复杂.文献［3-4］已经研究了加性高斯白噪声（additive white gaussian noise，AWGN）信道下的IR-UWB多用户系统的性能.但是由于超宽带信号的带宽很宽，因此如果多用户干扰相对于输出噪声可以忽略不计，则多用户系统差错概率就简化为单用户系统的差错概率，使计算变得简易.因此从理论上研究当多用户干扰相对于输出噪声能以高概率忽略不计时的大规模跳时IR-UWB网络所需的IR-UWB信号渐近带宽是非常有意义的.

在理论研究或仿真中，大规模网络的用户节点通常假设为随机分布，服从均匀分布或Poisson分布.文献［5］研究了用户节点服从Poisson分布时的IR-UWB信号渐近带宽.本文则将研究AWGN信道下用户节点服从均匀分布的IR-UWB信号渐近带宽.

式中：σmui和σn分别表示多用户干扰和噪声的方差；n表示网络内的用户数.

目前针对大规模无线网络的研究是学术界的一大热点［5－6］.通常有两种方法使大规模模网络内的用户节点数趋于无穷.一种方法是保持网络部署的区域为常数，而使用户密度ρ趋于无穷，这种网络称之为密集网络.另一种方法是保持用户密度ρ为常数，而使网络部署的区域趋于无穷，这种网络称之为扩展网络.本文将分别从理论上研究当多用户干扰相对于输出噪声能以高概率忽略不计时，用户服从均匀分布时的密集网络和扩展网络所需的IR-UWB信号渐近带宽.

关于无线网络的研究目前绝大多数集中在基于地面模型的二维空间，但是当网络部署在海洋或大气中时二维空间模型不再适用，需采用三维空间模型.三维无线网络具有广泛的应用，如视频监控、海洋采样和环境监控等，因此三维空间的无线网络近来也获得了关注［7－9］.本文将先研究大规模三维异步IR-UWB多用户系统的IR-UWB信号渐近带宽，然后再给出大规模二维异步IR-UWB多用户系统的IR-UWB信号渐近带宽.

跳时IR-UWB传感网已成为目前研究热点之一［9－10］，由于无线传感网的特点之一是节点数量众多，因此文中得到的结论有利于大规模跳时IRUWB传器网的性能，如生命周期、容量等，以及大规模跳时IR-UWB传器网的跨层协议设计的研究.

所谓“多用户干扰（MUI）相对于输出噪声以高概率忽略不计”，用数学公式可表示为

1 跳时IR-UWB多用户系统性能分析

考虑由n个用户节点组成的基于脉冲极性随机化的跳时IR-UWB多用户系统，采用BPSK（binary phase shift key）调制，AWGN信道，噪声的功率谱密度为η.假设路径损耗大小与收发信机之间距离的α次方成正比，其中α为路径损耗指数，α＞3.因为如果α≤3，且用户节点在空间均匀分布，则当网络内的用户节点数增加时多用户干扰将趋于无限大.

由文献［11］可知，相关接收机的输出包括对发射用户Xi的有用信号，多用户干扰和输出噪声.其中接收机输出的多用户干扰的表达式为

式中：是用户Xk发射的脉冲到达其接收用户处的接收脉冲能量；M（k）表明干扰用户Xk对有用信号的干扰.

在系统中所有用户完全同步情况下，若所有用户分配到的跳时序列全部正交，则＝0.但在一般情况下，通常需要考虑异步情形，此时多用户干扰将降低系统性能.为了便于分析，假定异步UWB多用户通信系统为码片同步系统，此时不同用户的符号是不重合的，但是不重合的距离是码片间隔Tc的整数倍.

由文献［11］引理3.1可知，当→∞，多用户干扰的方差为

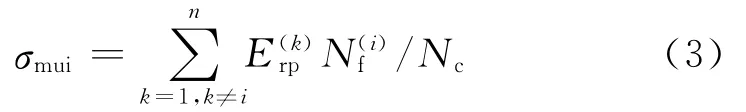
式中：为用户Xi的每比特发射的脉冲个数；Nc为每帧包含的码片数.

接收机输出噪声的方差为

式中：η已考虑了天线增益和线路损耗等.

接收到的有用信号能量Eb为

当IR-UWB信号的带宽足够大以致能满足多用户干扰相对于输出噪声可以忽略不计时，则接收用户对于发射用户Xi的差错概率为

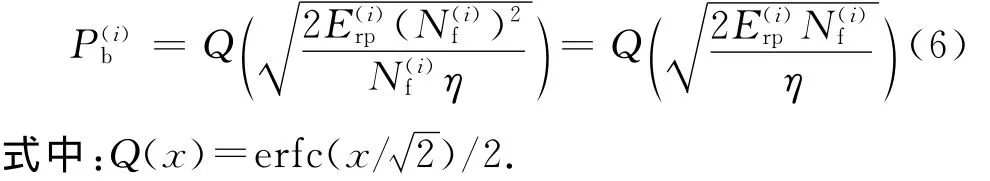
由式（3）可知，为了得到多用户干扰的大小，需要先研究均匀分布网络中用户节点的空间布置及网络中任意两个用户之间的距离.

2 三维空间棋盘形布置

对于三维密集网络，n个用户独立同分布且均匀地位于一个体积为V的立方体D中，其中V是一个与n无关的常数；对于三维扩展网络，n个用户独立同分布且均匀地位于体积为V＝λn的立方体D中，其中λ是一个与n无关的常数.

为了便于分析，引入一个关于立方体D的空间棋盘形布置T.空间棋盘形布置T由许多边长为l的小立方体d组成.每一个小立方体d为一个单元，称包含立方体D中心的单元称为中央单元.

如果两个单元之间共享一条边或一个顶点，则称这两个单元是邻接的.定义与中央单元相邻接的单元集合为立方环（annulus）A1，使用Ai（i＞1）表示围绕Ai－1的单元集合.显然立方环具有下述性质：

（1）在立方环Ak中单元数Zk为

（2）完全覆盖立方体D所需的环数τ必须满足

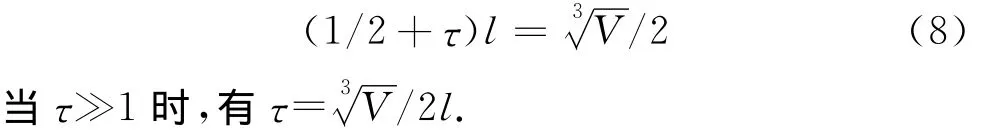
引理1 如果体积为V（与n无关的常数）的立方体D采用立方体棋盘格子T来覆盖，且每个小立方体单元d的体积为v（n）＝γ1Vlogn／n，则每个单元的用户节点数N（d）以高概率（即概率趋于1）满足N（d）≥1，且N（d）＝Θ（γ1logn），其中γ1是一个与n无关的常数.

证明 由于用户节点是独立同分布且均匀位于体积为V的立方体D中，因此对于一个特定的用户节点Xi，1≤i≤n落入一个特定单元的概率为

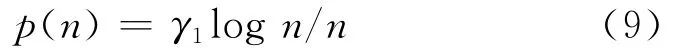
由此得到某个特定单元不含用户的概率是（1－p（n））n.

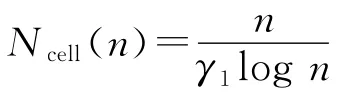
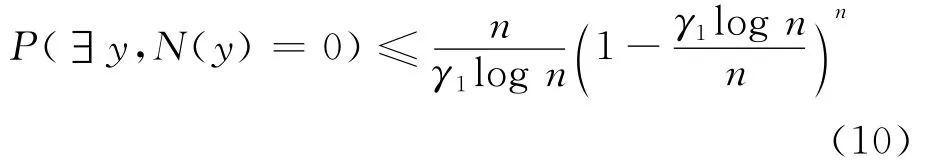
式中：y表示单元；N（y）表示在单元y中的用户数.因此

即，当n→∞和γ1＞1时，每个单元至少包含一个用户节点的概率趋于1.

根据式（9），可知一个单元内的平均用户数为u＝γ1logn.应用Chernoff界［12］，对单元y包含的用户数有

应用联合界有

因此当γ1＞8时，每个单元包含的用户数为Θ（γ1logn）的概率趋于1.

引理2 如果体积为V＝λn的立方体D采用立方体棋盘格子T来覆盖，且每个小立方体单元d的体积为v（n）＝γ2log（λn），则每个单元所包含的用户节点数N（d）以高概率满足N（d）≥1，且N（d）＝Θ（γ2logn），其中γ2是一个与n无关的常数.

证明过程类似于引理1，故证明略.

3 三维空间的任意两个用户之间的最小欧几里德距离

考虑到干扰大小与干扰用户和被干扰用户之间的距离有关，为了得到总的多用户干扰的大小，还需要研究均匀分布网络中任意两个用户之间的距离.

引理3 假设n个用户均匀且独立地分布在体积为V的立方体中，且V为常数，则对于任意与n无关的常数δ＞0，任意两个用户之间的最小欧几里德距离dmin满足

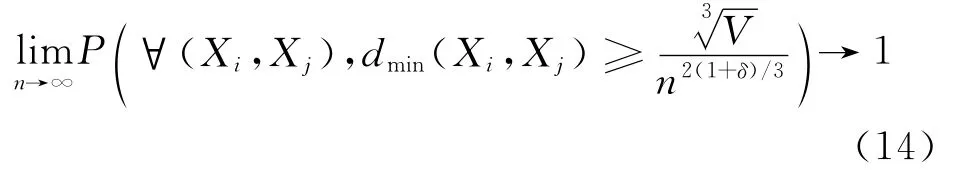
式中：δ＞0是一个与n无关的常数，Xi，Xj∈｛X1，X2，…，Xn｝且i≠j.

证明 设一个特定的用户X0与系统中的其他n－1个用户之间的最小欧几里德距离dmin大于等于为一事件，这事件等价于以用户X0为球心，半径为的球内没有其他用户.因此该事件发生的概率为.易知，以用户X0为球心，半径为的 球 内 有 其 他 用 户 的 概 率 为

因此，当n→∞且δ＞0时，密集网络内任意两个用户之间的最小欧几里德距离大于等于的概率趋于1.

引理4 假设n个用户均匀且独立地分布在体积为V的立方体中，且V＝λn，λ为常数.则对于任意与n无关的常数δ＞0，任意两个用户之间的最小欧几里德距离dmin满足

式中：Xi，Xj∈｛X1，X2，…，Xn｝，且i≠j.

证明 类似于引理3的证明.

4 三维异步跳时IR-UWB多用户系统的UWB信号渐近带宽

定理1 对于密集三维异步跳时IR-UWB多用户系统，n个用户节点在体积为V的立方体内服从均匀分布，当IR-UWB信号的渐近带宽为W（n）＝Ω（n2α（1＋δ）／3－1logn）时，则多用户干扰相对于输出噪声就能以高概率忽略不计，其中α＞3，n→∞.

证明 由引理1可知，当单元体积为v（n）＝γ1Vlogn／n时，则每个单元内的用户数以高概率满足N（d）＝Θ（γ1logn）.不失一般性，假设用户Xe在接收用户Xi发送的有用信号，并设用户Xe所在的单元为d0，则由式（3）可知，来自于单元d0及与d0邻接正方环单元内的多用户干扰的方差为

式中：常数27是源于与单元d0的邻接单元数为26得到的，t1是一个与n无关的常数.

由于

在不考虑天线响应的频率相关性时，接收功率可以表示为

式中：Pt是用户的发射功率；d为收发用户之间欧几里德的距离；α为路径损耗指数.

式中：t2是一个与n无关的常数.

因此，用户Xi收到总的多用户干扰为

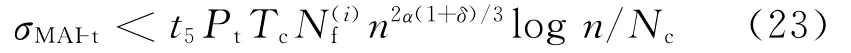
式中：t5是一个与n无关的常数.

考虑到在多用户系统中，每个用户都能有特定的TH码与之对应，因此每帧中包含的码片数至少为系统中的用户数，即有Nc≥n.

又由于码片时间宽度的倒数为IR-UWB信号的带宽，因此当式（23）远远小于式（4）时，即IR-UWB信号的渐近带宽满足W（n）＝Ω（n2α（1＋δ）／3－1logn）时，则多用户干扰相对于输出噪声就能以高概率忽略不计，其中α＞3，n→∞.

定理2 对于扩展三维异步跳时IR-UWB多用户系统，当IR-UWB信号的渐近带宽为W（n）＝Ω（nα（1＋2δ）／3－1logn）时，则多用户干扰相对于输出噪声就能以高概率忽略不计，其中α＞3，n→∞.

证明 类似于定理1，不同的是此处证明需要使用引理2和引理4.

5 二维异步跳时IR-UWB多用户系统的UWB信号渐近带宽

根据三维多用户系统IR-UWB信号的渐近带宽的研究思路和理论推导过程也可以得到大规模二维异步IR-UWB多用户系统的IR-UWB信号的渐近带宽.下面直接以定理形式给出.

定理3 对于密集二维异步跳时IR-UWB多用户系统，n个用户节点在面积为S的正方形内服从均匀分布，当IR-UWB信号的渐近带宽为W（n）＝Ω（nα（1＋δ）－1logn）时，则多用户干扰相对于输出噪声就能以高概率忽略不计，其中α＞2，n→∞.

定理4 对于扩展二维异步跳时IR-UWB多用户系统，n个用户节点在面积为λn的正方形内服从均匀分布，当IR-UWB信号的渐近带宽为W（n）＝Ω（nα（1＋2δ）／2－1logn）时，则多用户干扰相对于输出噪声就能以高概率忽略不计，其中α＞2，n→∞.

6 结论

研究了在AWGN信道下用户节点服从均匀分布的大规模异步跳时IR-UWB多用户系统中，当多用户干扰相对于输出噪声以高概率忽略不计时不同网络类型所需的IR-UWB信号渐近带宽.其中三维密集网络所需的IR-UWB信号渐近带宽为W（n）＝Ω（n2α（1＋δ）／3－1logn），三维扩展网络所需的IR-UWB信号渐近带宽为W（n）＝Ω（nα（1＋2δ）／3－1·logn），不同于n个用户节点分布在二维空间时所需的IRUWB信号渐近带宽.

文献［5］则研究了在AWGN信道下用户节点服从Poisson分布的大规模异步跳时IR-UWB多用户系统中，当多用户干扰相对于输出噪声以高概率忽略不计时不同网络类型所需的IR-UWB信号渐近带宽.通过比较可知，用户节点服从均匀分布时所需的IR-UWB信号渐近带宽与用户节点服从Poisson时所需的IR-UWB信号渐近带宽不同，因此IR-UWB信号的渐近带宽与节点的分布行为有关.

本文只研究了AWGN信道下的IR-UWB信号渐近 带宽，IEEE 802.15.4a和IEEE 802.15.3a UWB两种信道下的IR-UWB信号渐近带宽值得进一步研究.

［1］ Win M Z，Scholtz R A.Ultra-wide bandwidth time-hopping spread-spectrum impulse radio for wireless multiple-access communications［J］.IEEE Transactions on Communications，2000，48（4）：679.

［2］ Nekoogar F.Ultra-wideband communications：fundamentals and applications ［M］.Upper Saddle River：Prentice Hall，2005.

［3］ Fishler E，Poor H V.On the tradeoff between two types of processing gains［J］.IEEE Transactions on Communications，2005，53（10）：1744.

［4］ Gezici S，Molisch A F，Poor H V，et al.The tradeoff between processing gains of an impulse radio UWB system in the presence of timing jitter ［J］.IEEE Transactions on Communications，2007，55（8）：1504.

［5］ XU J.Asymptotic signal bandwidth of impulse radio UWB communication networks ［C］／／ Proceedings of the Global Communications Conference （GLOBECOM）. New York：IEEE，2011：1-6.

［6］ Wang C，Jiang C J，Li X Y，et al.General capacity scaling of wireless networks.IEEE INFOCOM，New York：IEEE，2011.

［7］ Bai X L，Zhang C L，Xuan D，et al.Low-connectivity and fullcoverage three dimensional wireless sensor networks ［C］／／Proceedings of the Tenth ACM International Symposium on Mobile Ad Hoc Networking and Computing（MobiHoc）.New York：ACM，2009：145-154.

［8］ Rainer M，Washington O，Gary B，et al.3D wireless network localization from inconsistent distance observations ［J］.Ad Hoc ＆Sensor Wireless Networks，2007，3（2／3）：141.

［9］ Xu J，Hong Y F，Jiang C J，et al.Energy dissipation bounds on three dimensional UWB wireless sensor network［J］.Journal of Software，2007，18（10）：2645.

［10］ Stoica L，Rabbachin A，Repo H O，et al.An ultra wideband system architecture for tag based wireless sensor networks［J］.IEEE Transactions on Vehicular Technology，2005，54（5）：1632.

［11］ Gezici S，Kobayashi H，Poor H V，et al.Performance evaluation of impulse radio UWB systems with pulse-based polarity randomization in asynchronous multiuser environments［C］／／Proceedings of IEEE Wireless Communications and Networking Conference（WCNC）.New York：IEEE，2004：908-913.

［12］ Michael M，Eli U.Probability and computing：randomized algorithms and probabilistic analysis ［M］. Cambridge：Cambridge University Press，2005.