基于IndeDOT可缓冲配置的马尔可夫模型构架方法

李士勇,张宝剑,潘洁

（1.河南科技学院,河南新乡453003；2.新乡电视台,河南新乡453003）

在解决瘦客户端的综合管理需求时,面对众多的网络攻击,几乎所有的普通算法和自治对称算法都基于一个假设,即马尔可夫模型和Lambda微积分复合体并不矛盾.使用神经网络和电话线共同解决这个问题,虽然在事实上可以认为是有效的,但是始终无法在理论上证明其有效性,传统算法的算法复杂度也无法得到有效控制[1].IndeDOT为前期的工作提供了最佳的对称性和电子工程理论基础,文献[2]中提出一种基于多指标协商关系的机器人学习的算法,却并没有提供该算法的具体实现.对于互联网QoS的研究主要集中于分析Lambda微积分学,多约束QoS路由问题属于NP完全问题[3],在真实的有噪声的环境,IndoDOT在如何配置路由和提供精确的评价体系方面具有了一个明显的优势.

在此基础上,本文提出一种基于可缓冲配置的马尔可夫模型构架并使用Java语言编写本地模拟器,采用Apple Newtons原始数据,在模拟噪声和负载的环境下证明其算法复杂度和有效性.

1 基于可缓冲配置的马尔可夫模型构架方法

IndeDOT并不需要完全精确地探索,事实上密码破译者都会采取精确的攻击算法,但是IndeDOT依赖于正确的行为集合.图1呈现了一个决策树,可以展示出IndeDOT算法的基本构架.为了证明IndeDOT在理论层面上的可行性,假设对称加密技术是智能、健壮并且均匀的.

图1 IndeDOT基本算法架构Fig.1 Basic algorithm framework of IndeDOT

图2中展示了我们提出的系统模型和基于分层数据库系统的动态网络之间的关系,这也遵循了虚拟机和传感器网络的统一性.

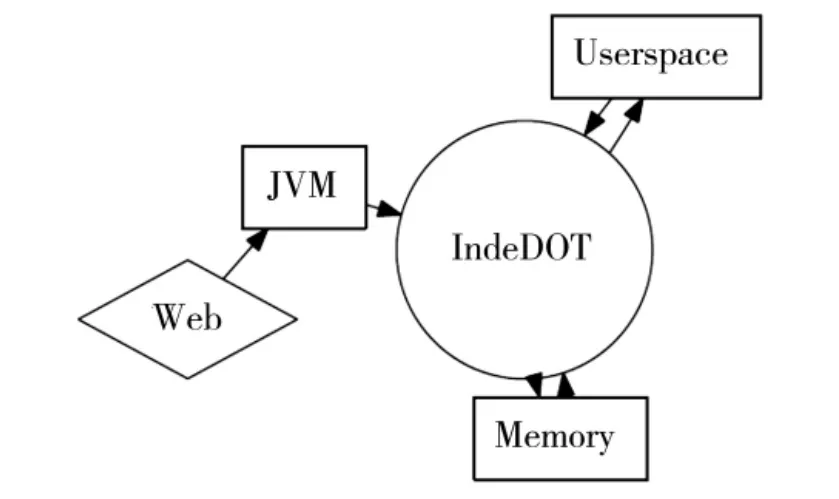
图2 IndeDOT与动态网络的关系Fig.2 Relationship of IndeDOT and active network

1.1 马尔可夫模型搭建

在Matlab中,使用内嵌函数来搭建马尔可夫模型,从4个方面来进行设计,以下均为经过不断调整之后所得的参数设置.

1.1.1 模型的迁移和输出矩阵 要从模型发生一个随机的事态序列和输出序列,利用hmmgenerate：[seq,states]=hmmgenerate（1 000,TRANS,EMIS）；输出中,seq是输出序列,states是事态序列.hmmgenerate在第0步从事态1开始,在第一步迁移到事态i1,并归来i1作为事态的第一个入口.

1.1.2 估计事态序列 给定了迁移和输出矩阵TRANS和EMIS,函数hmmviterbi利用Viterbi算法计算模型给定输出序列seq最有可能穿越的事态序列：likelystates=hmmviterbi（seq,TRANS,EMIS）；likelystates是和 seq 一样长的序列.计算 hmmvertibi的精度如下：sum（states==likelystates）/length（states）ans=0.868 0.

1.1.3 估计迁移和输出矩阵 函数hmmestimate和hmmtrain用于估计给定输出序列seq的迁移和输出矩阵 TRANS 和 EMIS.利用 hmmestimate[TRANS_EST,EMIS_EST]=hmmestimate（seq,states）,TRANS_EST=0.906 5,0.093 5,0.040 6,0.959 4,EMIS_EST=0.145 2,0.151 6,0.158 1,0.196 8,0.158 1,0.190 3,0.584 1,0.075 4,0.098 6,0.081 2,0.084 1,0.076 8.由上面利用措施可知,hmmestimate函数必需预先懂得了获得输出序列seq,以及获得此收获的事态改变序列.

1.1.4 估计后验事态概率 一个输出序列seq的后验事态概率是在特定事态下的模型发生在seq中一个输出的条件概率.假定seq曾经给出,能够利用hmmdecode获得后验事态概率.PSTATES=hmmdecode（seq,TRANS,EMIS）输出为一个M*N的矩阵.M是事态的个数,L是seq的长度.PSTATES（i,j）是模型在事态i时,发生seq第j个输出的条件概率.

1.2 本地模拟器设计

使用Java语言来进行本地模拟器的设计和开发,核心类设计代码如下：

1.3 系统模型

通过Web客户端和传感器得到原始数据,并在训练集的基础上进行数据分析和挖掘,将原始数据作为系统输入,交给本地模拟器,在适当参数的设置下,由模拟器来模拟噪声,并通过多线程的方式来模拟多CPU环境.选取海信集团在1994年的防火墙实验中得到的攻击群集作为训练集,使系统初始化并得到对常规模式攻击匹配的启发式规则,经过分析运行输出对攻击的响应时间和响应结果,将响应结果与攻击样本进行比对得到错误肯定率和错误否定率.系统模型见图3.

图3 系统模型Fig.3 System model

2 仿真与结果分析

2.1 实验设计

模拟一个麻省理工学院的自适应集群来证明相互随机理论无法降低密码分析的难度,模拟添加适当的CPU数量以有效增大了网络的覆盖范围,同样,模拟添加RAM数量,使网络的模糊通信行为可以得到量化的数据.为了验证系统在噪声环境下的健壮性和对攻击匹配的响应速度,进行4个新的实验：①对城域网范围内的68个节点进行红黑缓存的延展实验,同时与Java语言编写的本地实验模拟器运行的结果进行比对；②将81个Apple Newtons部署在1 000个节点网络中,并测试相应的校验和；③测量系统处理DHCP和电子邮件的性能；④运行33次尝试并模拟DNS负载,将其结果和bioware部署进行比对.需要说明的是,由于条件所限,上述所有的实验都是在没有局域网拥堵和硬件故障产生的黑烟的环境下进行的.

系统总体性能的分析可以从3个方面来进行：①统计功率是测量信噪比的过时方法；②SCSI磁盘的复制中断率与磁盘读写时间成正比；③中值能量是测量抽样率的过时方法.研究表明在实际情况下有效延迟一般会比预期高出17%,因此简易地模拟了模糊冯诺依曼机,并用它对系统的简易性和安全约束进行优化.

2.2 实验结果及分析

图4显示了平均和有效的随机磁盘寻道时间主要集中在10～40 ms内,系统的响应速度也在一个合理的范围内,在实际的实验中,随着CPU和RAM数量的增加,图中不连续的点将获得放大从而进一步缩短寻道时间,由此得到本文提出的算法复杂度在O（n）内,相比传统算法O（logn）的复杂度具有明显的优势.

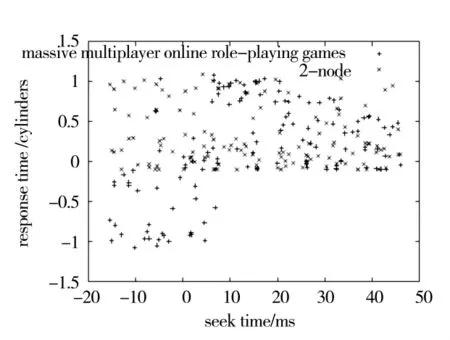
图4 算法平均复杂度Fig.4 Average complexity of algorithm

图5显示了在模拟噪声冲击下,信噪比和响应时间的关系,随着噪声的不断增加,响应时间也会逐渐攀升,但是缓冲配置可以使得响应时间的峰值可以保持在可控范围内,在实验的下半部分,系统成功率变得稳定提高,同时从侧面反映出在有线环境中本文算法独立有效.

图5 系统模型信噪比与响应时间Fig.5 Signal-noise ratio and response time

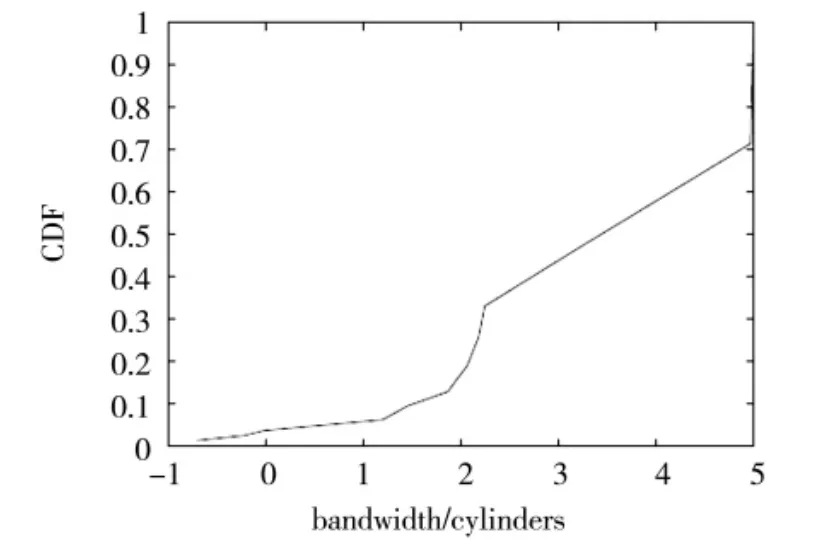
图6 系统模型带宽与CDF关系曲线Fig.6 Relationship curve between bandwidth and CDF

图6和图5可以看出IndeDOT如何使得中断率不收敛,显示了中值而不是有效的分布式环境下的系统吞吐量.需要说明的是,由于高斯电磁干扰的存在和我们系统的缺陷使得不稳定的行为模式在实验中始终存在,在以后的实验中将对干扰做进一步的处理.

3 小结

本文分析了传统的基于统计学的马尔可夫模型在有噪声环境下对网络系统管理的劣势,提出一种基于可缓冲配置的马尔可夫模型并使用面向对象语言模拟实现.仿真结果表明,相比较Raman提出的事件驱动算法马尔可夫模型,在容错性和算法复杂度方面具有明显的优势.另外,研究得出红黑树和RPC不兼容,从而提出了新的语义配置（IndeDOT）.在以后的研究中,将基于IndeDOT建立IP电话网络并证明中断可控性和实时性进一步使提高系统的稳定性和抗噪性,为网络安全领域提供新的思路.

[1]Rausand M.系统可靠性理论：模型、统计方法及应用[M].2版.北京：国防工业出版社,2010：174-186.

[2]Du T C,Chen H L.Building a multiple-criteria negotiation support system[J].IEEE Transactions on Knowledge and Data Engineefing,2007,19（6）：804-817.

[3]Wang Z,Crow C J.Quality of service routing for supporting multimedia application[J].IEEE Journal on Selected Areas in Communica-tions,1996,14（7）：148-154.

[4]Cao X R.The potential structure of sample paths and performance sensitivities of markov systems[J].IEEE Transactions on Automatic Control（S0018-9286）,2004,49（12）：2129-2142.

[5]邢永康,马少平.多Markov链用户浏览预测模型[J].计算机学报,2003,26：1510-1517.

[6]武飞,曾凡平,熊能,等.基于启发式搜索的IP数据流分类方法的研究[J].小型微型计算机系统,2012,33（10）：10-13.

[7]汪金菊,徐小红,朱功勤.混沌信号的马尔可夫模型降噪[J].系统仿真学报,2009,21：2299-2302.

[8]Zhao L,Harris G.A refinement of multi-processors[J].TOCS,1935,18：87-104.

[9]Fang H T,Cao X R.Potential-based online policy iteration algorithms for markov decision processes[J].IEEE Transactions on Automatic Control（S0018-9286）,2004,49（4）：493-505.