基于随机Petri网的流通加工系统建模研究

李小鹏，李孝忠

(天津科技大学计算机科学与信息工程学院，天津 300222)

流通加工系统是库存系统的一个关键环节，所谓流通加工，就是物品从生产到使用的过程中，根据客户需要所施加的组装、包装、分割、计量、分拣、贴标签、分装等简单作业的总称，是对生产加工的一种补充．常见的流通加工有冷冻加工、分选加工、精制加工、分装加工、组装加工．本文研究的是精制加工，主要包括产品的清洗、加工、包装等步骤．

Petri网的图形表示和描述异步并发的能力为系统的建模提供了强有力的帮助．随机 Petri网(stochastic Petri net，SPN)[1]是在 P/T 网的基础上，对每个变迁相关联一个服从指数分布的实施速率，它是用来描述动态行为同构于连续时间马尔科夫链(Markov chain，MC)的离散动态系统的，并被广泛应用于通信、同步等问题[2]，然而相关研究所处理的系统大多是精确系统，有一定的局限性．

流通加工系统是一个动态离散系统，为了得到更精确的数值解，使系统的性能分析结果更符合实际，本文将 SPN与模糊理论结合，提出一种新的建模与分析方法，即基于模糊参数的 SPN(stochastic Petri net with fuzzy parameter，SPNFP)，并以三华农副产品加工基地农副产品的一次流通加工为研究背景，建立流通加工系统的 SPN模型，对该系统进行了有效性分析(定性分析)和性能分析(定量分析)．有效性分析是基于 T_不变量和马尔科夫过程的分析；性能分析是基于模糊参数的 SPN的分析，其基本思想是给SPN模型中的每个竞争变迁分配一个模糊算子，对变迁实施速率模糊化，借助于连续时间的 SPN同构于连续时间马尔科夫链的特点得到系统的稳定状态概率方程组[3–4]，然后利用三角形隶属模糊数的运算规则得到稳定概率的信任区间，再用区域中心法得到精确解，最后对其进行性能分析．

1 基于模糊参数的随机Petri网

定义1 基于模糊参数的SPN是一个八元组

模糊引发率iλ˜可由三角形隶属函数[5]中三元组的最大隶属度，即来定义，其中参数2ia给出了参数1ia和3ia给出模糊数据的最小和最大限．

2 基于SPN的流通加工系统的实例建模

2.1 流通加工的流程

产品的流通加工过程是从农副产品进入系统开始的，主要包括卫生指标检测、清洗、加工、质量验收、包装5个步骤[6-7]，具体流程见图1．

图1 流通加工系统的流程图Fig.1 Flow chart of circulation processing system

2.2 建模

对图1所示的流通加工系统进行建模，其SPN模型如图2所示．模型中库所和变迁的含义如下：1P为农副产品到达仓库，准备加工；2P为产品的卫生检测完成；3P为产品等待清洗；4P为产品的清洗完成；5P为产品等待加工；6P为产品的加工完成；7P为产品等待质量验收；8P为产品的质量验收完成；9P为产品等待包装；10P为产品的包装完成；11P为产品的流通加工完成，等待后序工作；1T为按标准对产品进行卫生质量检测；2T为将不符合卫生指标的产品搬运至退货区；3T为将符合卫生指标的产品搬运至清洗区；4T为对产品进行清洗；5T为将清洗后的产品搬运至加工区；6T为对产品进行加工；7T为将加工后的产品搬运至验收区；8T为对产品进行质量验收；9T为将质量验收不合格的产品再次搬运至加工区；10T为将质量验收合格的产品搬运至包装区；11T为对产品进行包装；12T为将包装好的产品搬运至发货区，等待发货；为产品的流通加工全过程结束及信息反馈工作．

模型中的变迁2T和3T及9T和10T 均属于竞争关系[8]，根据该企业以往的统计资料可知，产品卫生指标检测合格的概率约为99.5%，产品加工质量合格的概率约为 99.9%．因此，对变迁3T赋予模糊算子为μ2,3=99.5%，对变迁T2赋予模糊算子为μ2,11=1−99.5%=0.5%；对变迁T10赋予模糊算子为μ8,9=99.9%，对变迁 T9赋予模糊算子为 μ8,5=1 − 9 9.9%=0.1%．

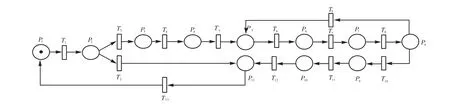
图2 流通加工系统的SPN模型Fig.2 SPN model of circulation processing system

3 模型的有效性分析和性能分析

3.1 模型有效性分析

3.1.1 基于T_不变量的模型有效性分析

首先得到模型的关联矩阵

由0×=CX得到T_不变量：

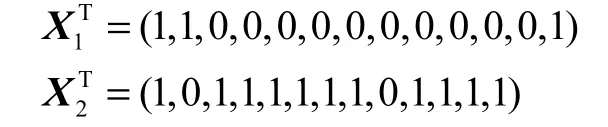
当分量为1时表示此变迁被触发，分量为0时表

由关联矩阵及T_不变量可得出如下结论：

(1)此过程中没有一个变迁(任务)没有输入条件或没有输出条件，它们都有各自的输入和输出库所，表明任何流通加工任务的完成都需要一定的条件.

(2)没有死任务，即没有永远不能执行的任务，竞争变迁2T和3T及9T和10T 是根据实际情况来判断的，其他结构均是顺序结构，这说明流通加工系统的各个子任务都会发生，这是流通加工工作可以顺利完成的前提．

3.1.2 基于马尔科夫过程的模型有效性分析

根据连续时间的 SPN同构于连续时间马尔科夫链的特点，可得到与SPN模型同构的马尔科夫链，如图 3所示．其中，马尔科夫链中的状态可达标识见表1，数字“1”表示库所中的托肯数(即库所中的标记数)为1，数字“0”表示库所中的托肯数为0．

表1 Petri网的状态可达标识Tab.1 State reachable marking of Petri net

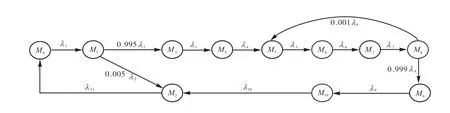
图3 模型的MCFig.3 MC of the model

由模型的 MC可知：(1)整个流程没有发生堵塞，托肯的流动是流畅的，流通加工过程最重要的因素仍然是时间因素．(2)整个流程中各个库所都至多有一个托肯，说明流程不会产生瓶颈．(3)不存在某种状态iM没有任何变迁可达，即没有一个状态永远不会发生，模型中不存在死锁．因此，所建模型是合理的．

3.2 模型性能分析

根据已有 MC可以得到马尔科夫过程的转移速率矩阵：

取稳定概率之和“1”的模糊数为(0.9,1,1.1)，令α为 0～1，步长为 0.1，利用三角形隶属模糊数的运算规则[5]，则可以计算出稳定概率的信任区间，结果见表2．

从而求得

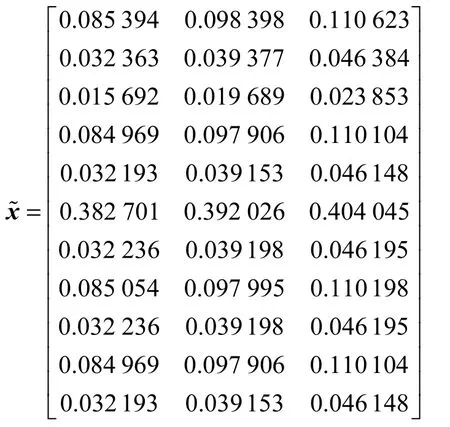
利用区域中心法[10]进行解模糊得：10.098138 x= ，

由此可以得到稳定概率如下：

P[M0]＝0.098,138

P[M1]＝0.039,375

P[M2]＝0.019,745

P[M3]＝P[M9]＝0.097,660

P[M4]＝P[M10]＝0.039,165

P[M5]＝0.392,924

P[M6]＝P[M8]＝0.039,210

P[M7]＝0.097,749

根据求得的稳定概率可以计算出系统性能的指标，包括库所繁忙的概率、系统变迁的利用率、系统平均延时时间、流入系统的标记流速．

表2 稳定概率的信任区间Tab.2 Confidence interval of stable probability

3.2.1 库所繁忙的概率

库所繁忙的概率就是各流通实体所处于忙碌状态的概率，经计算得

P[M(P1)＝1]＝P[M0]＝0.098,138

P[M(P2)＝1]＝P[M1]＝0.039,375

P[M(P3)＝1]＝P[M3]＝0.097,660

P[M(P4)＝1]＝P[M4]＝0.039,165

P[M(P5)＝1]＝P[M5]＝0.392,924

P[M(P6)＝1]＝P[M6]＝0.039,210

P[M(P7)＝1]＝P[M7]＝0.097,749

P[M(P8)＝1]＝P[M8]＝0.039,210

P[M(P9)＝1]＝P[M9]＝0.097,660

P[M(P10)＝1]＝P[M10]＝0.039,165

P[M(P11)＝1]＝P[M2]＝0.019,745

由此可知，状态5P的库所繁忙概率比较大，即产品的等待加工环节最容易产生信息的堆积，因此，可将加工环节作为优化的重点．

3.2.2 系统变迁的利用率

系统变迁的利用率，是使变迁可实施的所有标识的稳定概率之和．经计算得

U(T1)＝P[M0]＝0.098,138

U(T2)＝U(T3)＝P[M1]＝0.039,375

U(T4)＝P[M3]＝0.097,660

U(T5)＝P[M4]＝0.039,165

U(T6)＝P[M5]＝0.392,924

U(T7)＝P[M6]＝0.039,210

U(T8)＝P[M7]＝0.097,749

U(T9)＝U(T10)＝P[M8]＝0.039,210

U(T11)＝P[M9]＝0.097,660

U(T12)＝P[M10]＝0.039,165

U(T13)＝P[M2]＝0.019,745

从计算结果可知，变迁6T的利用率相对较高，即产品的加工过程相对耗时．因此，对加工环节的优化可以有效的提高整个流通加工系统的效率．

3.2.3 系统平均延时时间

根据 SPN 的简化规则[11]，可得整个流通加工系统的平均实施速率为

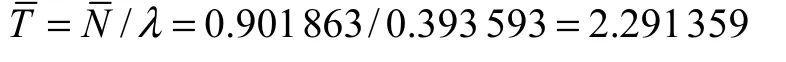
即系统平均工作时间为 2.291,359,h．这里的系统平均工作时间考虑了需要流通加工和不需要流通加工两种情况，而这两种情况是不可能同时发生的，但从系统分析角度计算时需要将两种情况同时考虑，所以实际流通加工时间应该小于系统平均工作时间，但仍可作为性能评价的依据．

3.2.4 流入系统的标记流速

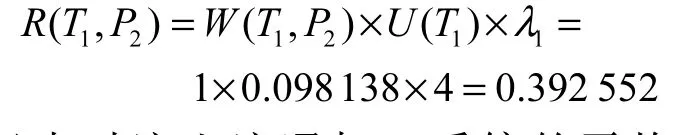
每小时流入流通加工系统的平均标记数为0.392,552，即有一个标记数流入流通加工系统需要2.547,433,h．对比系统平均工作时间 2.291,359,h可知，流入系统的标记流速还应适当加快，这样可以提高流通加工系统的效率．

4 结 语

本文以三华农副产品加工基地农副产品的一次流通加工为研究背景，利用 SPN及模糊相关理论对流通加工系统进行了定性分析和定量分析，验证了模型的有效性，并指出了流通加工过程中需要重点强化及完善的环节．

实际的流通加工过程中有多种农副产品，本文没有考虑不同农副产品的分拣过程，直接默认已经分拣好，考虑的是单一农副产品流通加工过程，以后需进一步研究不同农副产品的分拣过程，使加工基地的所有农副产品的流通加工都能顺利有序地进行．

［1］ 林闯. 随机 Petri网和系统性能评价[M]. 2版. 北京：清华大学出版社，2005.

［2］ 顾明甲，张伟，周青. 一种基于 Petri网的安全协议验证方法[J]. 微计算机信息，2010，26(5-3)：78–80.

［3］ Balbo G. Introduction to Stochastic Petri Nets[M].Berlin：Springer-Verlag，2001：84–155.

［4］ Chen S M. Weighted fuzzy reasoning using weighted fuzzy Petri nets[J]. IEEE Transactions on Knowledge and Data Engineering，2002，14(2)：386–397.

［5］ 杨纶标，高英仪，凌卫星. 模糊数学原理及应用[M]. 5版. 广州：华南理工大学出版社，2011.

［6］ 张春娜. 基于Petri网的物流仓储系统建模与仿真[D].南京：南京林业大学，2007：31–37.

［7］ 吴冰. 基于Petri网的物流中心库存建模和预测仿真的研究和实现[D]. 上海：上海交通大学，2008：15–21.

［8］ Colombo A G，Saiz de Bustamante A. Systems Reliability Assessment[C]. Dordrecht，the Netherlands：Kluwer Academic Publishs，1990：125–130.

［9］ 艾厚文. 基于随机Petri网的铁路应急预案流程化研究[D]. 北京：北京交通大学，2008：50.

［10］ 原菊梅，侯朝桢，王小艺，等. 基于随机 Petri网的可修系统可用性模糊评价[J]. 计算机工程，2007，33(8)：17–19.

［11］ 王伟，刘文菊，苏迪. 基于 Petri网的物流仓储系统的建模研究[J]. 2010，21(11)：95–98.