超空泡射弹尾拍力求解的一种改进型方法

张丁雄，侯健



超空泡射弹尾拍力求解的一种改进型方法

张丁雄1，侯健2

（海军工程大学，武汉 430033）

传统的超空泡射弹尾拍力求法将空泡边界看成是一条直线，在求解弹丸浸入长度时势必造成误差，导致弹丸的尾拍力求解不精确，本文主要在传统求解浸湿长度的基础上提出了一种改进型的求解方法，将空泡壁看成是椭圆的一部分。仿真结果显示，改进后尾拍力变大，弹丸衰减速度变快，弹丸空化器上的阻力变小。

超空泡 射弹 尾拍力 浸湿长度

0 引言

超空泡射弹空泡的运动轨迹、运动速度及弹体本身的动态响应等特性是超空泡射弹武器研制的关键和根本。射弹的无动力运动轨迹由水下惯性运动的稳定性决定，存速则由超空泡的减阻效果决定，弹体本身结构破坏和屈曲失稳是由射弹的模型设计、结构设计和材料选择决定。三者虽然反映出的分别是超空泡弹丸运动过程中的三个方面的问题，问题的角度不同但相互联系着，解决这些问题的关键都在于射弹带空泡运行时的力学分析。

超空泡射弹水中高速航行时的动力学计算包含了液体、气体、固体（弹丸）等多种介质的相互作用，其过程是非常强烈的非线性物理模型，很难用准确的数学语言进行描述。近些年来，国内外研究人员针对水下航行体的运动特性进行了不少的研究工作，麻震宇[1]针对超空泡航行体轴向的受力特点，建立了超空泡航行体双层壳结构的有限元模型，对结构动力稳定性进行了分析；范辉[2,3]根据圆判据研究了超空化航行器的稳定性及最优控制问题；易文俊[4]采用Fluent软件的两相流模型对带有尾翼弹丸的稳定性进行了模拟仿真分析；文献[5,6]中对水下射弹滑行力的计算进行了研究，并给出了一系列的经验公式。

1 弹丸运动学方程

设射弹绕流为理想可压缩流体无旋定常运动，为避免尾部空泡回注射流形成的数学奇异性，采用Riabushinsky空泡闭合方式（即空泡以与射弹对称的形式闭合），将坐标原点建立在空泡顶点处（图1）。

图1 超空泡外形

空泡外形方程为：

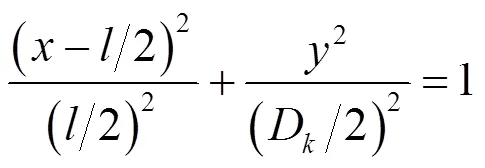
其中：——超空泡长轴；D——超空泡长轴。

射弹在控制面内，运动状态分为两个不同的阶段：

1）射弹还没有与超空泡壁发生碰撞

2）射弹的尾部与超空泡壁发生碰撞

在第一阶段，射弹只是前端受水的阻力，而第二阶段则其尾部也受力。碰撞力及力矩的计算是基于Milwitzky[8]的思想方法进行的；射弹前端所受的阻力是由Kiceniuk[9]的试验结果得来的；计算超空泡长度、最大直径等参数的公式由文献中方法给出。

在每根骨架上划出“十”字定位线，实际测量后，将数据与三维模型数据进行对比并对数据进行修正。最后，减去玻璃之间的离缝得出最终的玻璃尺寸。汇总玻璃数据信息提交专业生产厂家生产。

数学模型根据文献[10]的思想建模，本文建立的模型作如下假设：

1）射弹在纵向平面内做平面运动；

2）在控制面内，射弹绕空化器做平面内的转动；

3）射弹的运动不受超空泡中气体、水蒸汽和水滴的影响。

4）忽略重力对运动的影响。

图2 射弹受力示意图

第二个阶段可以写成：

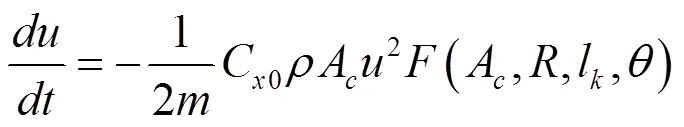
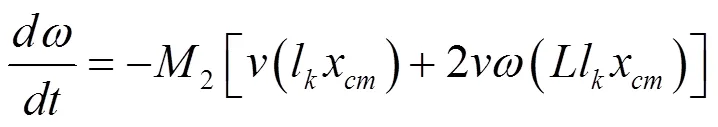
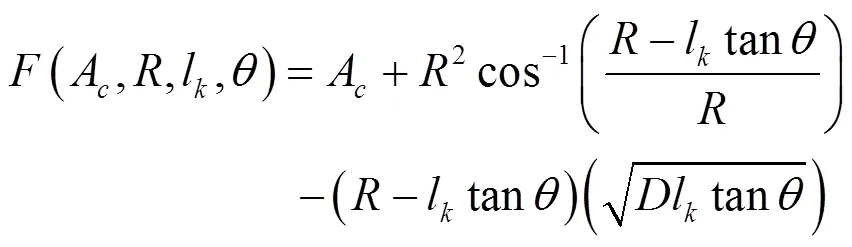
——分别为xy方向的速度

——弹丸转动角速度；

2 浸入长度求解

为了得到射弹在每个时刻所受的水的作用力和力矩，我们需要知道每个时刻它的浸入长度l。文献[11]给出了l的一种解法，如图3所示。

图3 射弹撞击超空泡边界图解

因此我们如要求t时刻点O浸入的深度，则可以用类似的方法，用t时刻的深度来求之。

例如：求2时刻的深度()：

()=()+() （8）

其中，()是在2时刻，()在与射弹的轴相垂直的直线上的投影。()是1到2时间内浸入深度的变化值。因此我们可以依次求下去直到深度为0。

这种方法将空泡的边界简单的看成是一条之间，求出的结果势必会带来误差，本节基于Salil提出的这种方法的基础上进行改进，使得解出的结果更加符合实际情况，如图4。

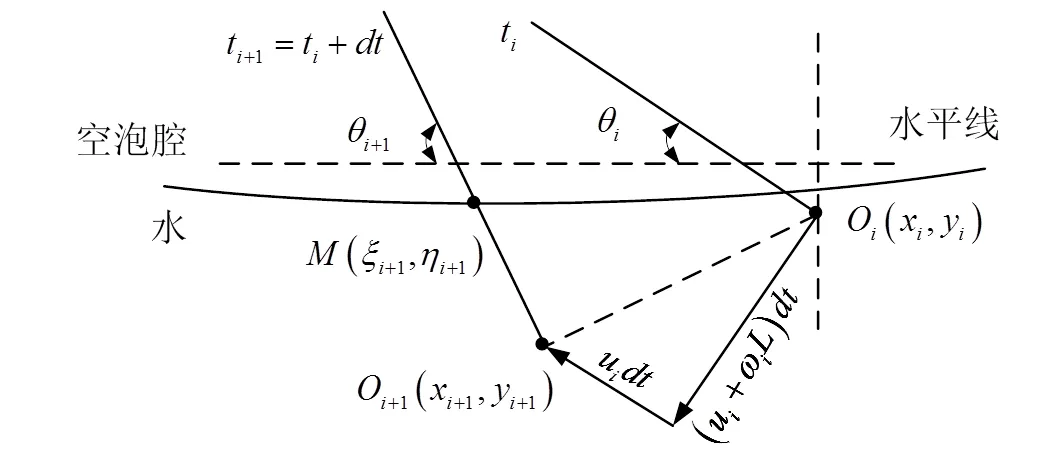
图4 空泡壁为椭圆时的两个时刻浸湿位置关系

本节将空泡壁看成是一条弧线，而不是直线，弧线为空泡外形的一部分，其形状由公式（1）给出。在t时刻浸湿长度为l()，t+1时刻浸湿长度为l(+1)，由图中可以看出O和O+1的位置关系有：

对于直线O+1有方程：

其中：

将式子（11）带入椭圆方程可以解得：

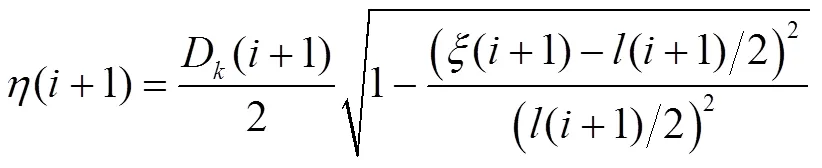
弹丸与空泡壁的交点(+1, η+1)的位置由式（13）和式（14）确定，故有：

3 仿真结果及分析

本文利用欧拉法对改进前后进行编程，仿真结果如图所示。

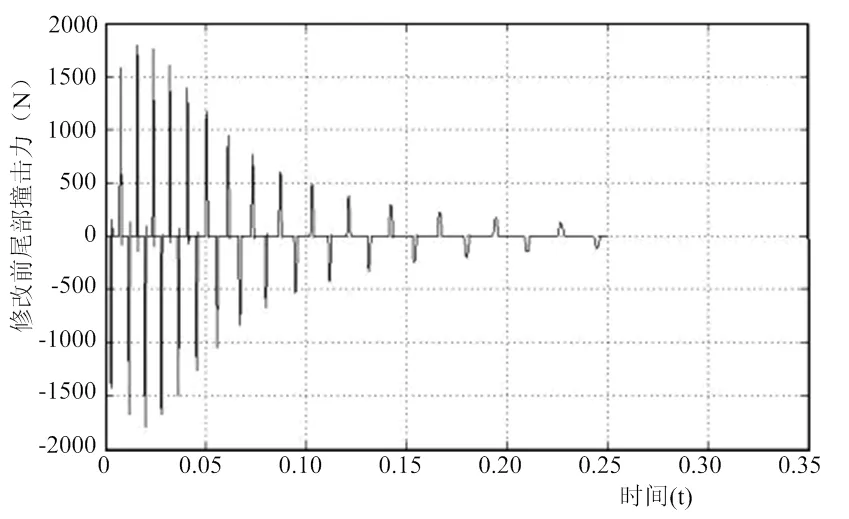
图5 改进前后各个物理量对比

图5中可以看出，改进后弹丸的衰减速度比原来更快，头部的空化器阻力刚开始没有发生变化，但是随后受到的力比改进前更小了；尾拍力比原来增大。造成这种不同的主要原因是由于改进前将空泡壁看成是一条直线，撞击点的空泡直径看成是弹丸尾部的对应的空泡处直径，且撞击点的纵坐标不再发生破坏，但是在真实的情况中，由于空泡壁时椭圆形的，弹丸与空泡壁相交地方纵坐标时发生变化的，随着撞击的深入，空泡壁是一个弧形，弹丸与空泡发生撞击的分界点处对应的空泡直径实际上是变小的，故实际的浸入长度比未改进前要大，所以弹丸发生撞击时将受到更大的撞击力（即尾拍力），弹丸速度衰减的更快，故空化器阻力也变小。

4 结束语

通过将平直的空泡壁变换成椭圆形，弹丸的浸湿长度变大了，使受到的尾拍力变大，弹丸速度衰减的更快，所以弹丸空化器上的阻力也减小了，仿真的结果更加符合实际情况，更加真实的反映弹丸在水中的运动情况。

[1] 麻震宇, 胡凡, 陈广南, 等. 超空化航行体双层壳结构动力稳定性分析[J]. 国防科技大学学报, 2011, 33(4): 43-47.

[2] 范辉, 张宇文. 超空化航行器稳定性分析及最优化控制设计[J]. 信息与控制, 2009, 38(4): 393-398.

[3] 范辉, 张宇文. 超空化航行器稳定性分析及其非线性切换控制[J]. 控制理论与应用, 2009, 26(11): 1211-1217.

[4] 易文俊, 张木, 陈志华, 等. 带尾翼高速射弹自然超空泡流特性硏究[J]. 南京理工大学学报, 2011(4): 178-186.

[5] Kulkarni S, Pratap R. Studies on the dynamics of a supercavitating projectile[J]. Applied Mathematical Modeling, 2000(24): 113-129.

[6] Maekey A M. A mathematical model of waterentry[R]. AUWE Technieal Note, 1979.

[7] Hassan S E. Analysis of hydrodynamic planing forces associated with cavity riding vehicles[J]. Private Communication, 2004, 7(4): 26-30.

[8] Milwitzky B. Generalized Theory for Seaplane Impact[R]. NACA-TR-1103, 1952.

[9] Kiceniuk T. An experimental study of the hydrodynamics Laboratory[C]. Calif-ornia Institute of Technology, 1954.

[10] Salil S, Kulkarni, Rudra P. Studies on the dynamics of a supercavitating projecttile[J]. Applied Mathematical Modelling, 2000, (24): 113-129.

[11] Salil S, Kulkarni, Rudra P. Studies on the dynamics of a supercavitating projectile[J]. Applied Mathematical Modelling, 2000, 24: 113－129.

An Improved Method to Solve Tail Shot Strive of Supercavitating Projectile

Zhang Dingxiong1, Hou Jian2

(Naval University of Engineering, Wuhan 430033, China)

TK05

A

1003-4862（2013）10-0047-04

2012-11-15

张丁雄(1988-)，男，硕士研究生。研究方向：武器系统仿真与试验技术。