导数有话说：物体是怎样运动的

毛金平

函数图像是函数的一种最形象、最直观的表示方法，而导数则是研究函数相关性质的一个有力工具。这里，我就从描述物体的运动状态、比较物体的运动状态、探究物体形状的设计三方面各举一例，带领大家通过观察函数图像，结合导数的几何意义，共同来探究事物的变化规律。

描述物体的运动状态

例1：“菊花”烟花是最壮观的烟花之一。制造时一般是期望在它达到最高点时爆裂。 如果烟花距地面的高度h（m）与时间t（s）之间的函数图像如图所示，试描述烟花升空后的运动状况。

【分析】要描述烟花升空后的运动状态，就得探究烟花升空后在不同时刻的瞬时速度的变化规律。结合导数的几何意义，就是要探究烟花距地面的高度h（m）与时间t（s）之间的函数图像上各点切线斜率的变化规律。

【解】由函数图像，结合导数的几何意义，我们可以看出：

在t=1.5s附近曲线比较平坦，也就是说此时烟花的瞬时速度几乎为0，达到最高点并爆裂；

在0～1.5s之间，曲线在任何点的切线斜率大于0且切线越来越“平缓”，也就是说烟花在达到最高点前，以越来越小的速率升空；

在1.5s后，曲线在任何点的切线斜率小于0且切线越来越“陡峭”，也就是说烟花达到最高点后，以越来越大的速率下降，直至落地。

比较物体的运动状态

例2： 两兄弟甲、乙同时从家里出发去游乐园，他们离家的距离s关于时间t的函数图像如右图所示，试根据图像比较他们在去游乐园途中运动状态的异同。

【分析】要看两兄弟在去游乐园途中的运动状态，直接分析他们离家的距离s关于时间t的函数图像在某点切线的斜率，即他们在任一时刻的瞬时速度即可。

【解】由函数图像，结合导数的几何意义，我们可以看出：

两兄弟从家里出发后，均以各自不同的速度前往游乐园；

对于甲来说，随着时间的推移，曲线切线的倾斜度先是不变，后是越来越“陡峭”，即甲先匀速前进，后以越来越快的速度向游乐园赶去；而对于乙来说，随着时间的推移，曲线切线越来越“平缓”，即乙是以越来越慢的速度向游乐园走去。

探究物体形状的设计

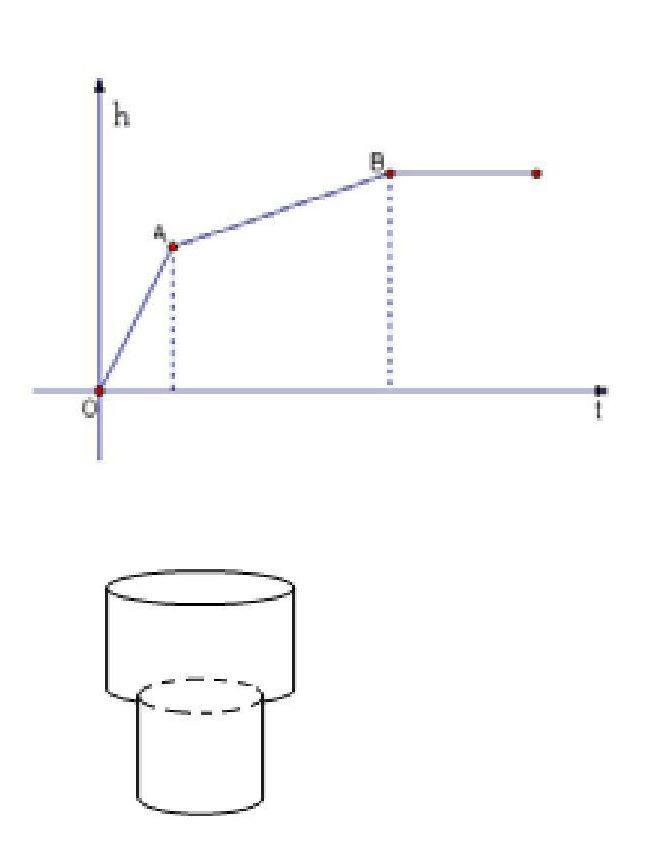
例3：设计一个杯子的形状，使得在向杯中匀速注水时，杯中水面的高度h随着时间t变化的图像与上面右图的图像相符合。

【分析】由图可以看出，无论是在OA段还是在AB段，水面的高度都在均匀增加，不同的是AB段比OA段要“平缓”，也就是说，在OA段的时候高度增加得快，而在AB段的时候高度增加得慢。

【解】由题意知，我们可以将杯设计成上粗下细，如下面右图所示：

小结：利用导数探究事物的变化规律，其关键就是抓住导数的几何意义，即函数f（x）在x=x0的导数就是曲线y=f（x）在点P（x0，f（x0））处的切线的斜率。当函数图像上曲线切线越来越“陡峭”且斜率大于0，或曲线切线越来越“平缓”且斜率小于0时，函数在此处的导数越来越大；反之，当函数图像上曲线切线越来越“陡峭”且斜率小于0，或曲线切线越来越“平缓”且斜率大于0时，函数在此处的导数越来越小。

封面镜头

上海交通大学老图书馆秘境

“不进徐家汇的门，不算交大人”，去上海交通大学徐汇校区，一定不能错过老图书馆。建于1919年的老图书馆座东朝西，是一幢三层的混合结构建筑，整个建筑由红砖砌成，带有英国伊丽莎白时代的建筑风格。大楼的平面设计为“山”字形，整体比例对称。立面楼体上的山墙醒目，底楼的门廊突出，门廊里有两对科林斯双柱支撑着二楼的露台。二楼的窗体采用弧拱形，西部有华丽的巴洛克式雕刻。整个建筑浑然一体，设计上摆脱了早期古典主义的拘谨，显得更为活泼轻松。

交大历来教学严谨，学生个个勤奋好学，老图书馆便是最好的“见证人”。除了作为藏书楼之外，老图书馆还曾扮演过宿舍的角色。抗战刚胜利时，交大校园遭到严重破坏，甚至没有专门的宿舍。正好图书馆是空的，所以学生就住在图书馆一楼，在整个大厅里一排排地放着单层床铺。那时虽然物质条件很差，但学生士气很高，读书都很用功。

今天的老图书馆也没有书了，放的都是卷宗，它已经成为上海交大的档案馆。在那里，能翻看到一张泛黄的工工整整的满分“水力学”考卷，署名是“钱学森”。仔细看，考卷右上角分数栏里填写的“100分”旁，又有一个“96分”。原来是钱学森在一处连续等式后将“Ns”简为“N”，老师未算错，钱老本人要求扣分，老师最后就给了他96分。还有在交大读书读到吐血的著名校友。比如邹韬奋，在交大读土木时由于交大理工科要求严格，读到半夜，一口鲜血喷在书本上，读不下去了，只好转学到圣约翰大学去学新闻。要是邹韬奋当时没有跑掉，不知道中国近代史上会不会少一位著名记者，而多一位科学家。