张力腿平台系泊系统特性研究＊

黄 佳 肖龙飞 谢文会 寇雨丰

（1.中海油研究总院； 2.上海交通大学海洋工程国家重点实验室）

张力腿平台（TLP）是目前深海油气开发常用的生产平台之一，其在六自由度上的固有频率避开了海洋波浪的主要频率，可以有效避免在波浪中的共振现象，减小在波浪中的运动响应，目前在国外已得到广泛运用，而在国内还没有运用到工程实际中。在当前我国将要对南海深水油气进行开发的形势下，对张力腿平台进行相关研究并做好充足的技术储备具有重要的现实意义。

TLP采用垂直张紧式系泊系统，相对于传统的悬链线、张紧式系泊系统有较明显的区别。对于张力腿本身而言，其需同时满足一阶及二阶可靠性条件。Federico［1］曾通过一种基于蒙特卡洛法的概率分析法对TLP系泊张力腿进行可靠性分析；由于长度及重量的增加，张紧索系统的自振频率降低，较大可能产生浮体与张紧索的耦合振动，Jayalekshmi［2］设计了一个对比试验来研究TLP的浮体与张紧索的耦合振动。另外，也有一些学者对TLP系泊系统做了一些前沿性的研究，比如Chan［3］通过数值模拟方法研究张力腿在平台运动时出现的瞬态脱离所带来的影响；Bian［4］提出一种适应极深水深的TLP系泊系统方案，在立柱内安装一充气式的振动吸收装置，通过相位补偿的原理减小了垂向振动，降低了张力腿垂向刚度的要求。

本文重点对TLP垂直张紧式系泊系统进行研究。一方面，由于通用的系泊静力分析软件（如Dynfloat等）不支持对垂直张紧式系泊系统进行分析，而耦合分析软件（如Sesam）则较为费时，因此，笔者提出一种较为简化的静力分析方法来分析TLP垂直张紧式系泊系统的静力特性，与模型试验结果吻合良好；另一方面，通过对比数值分析与模型试验的结果来研究TLP垂直张紧式系泊系统的动力特性。

1 TLP及系泊系统参数

TLP由8根张力腿垂直系泊，平台中央布置9根张紧式立管。立管对系泊系统特性产生直接影响，因此文中将立管与系泊系统一起考虑分析。TLP及系泊系统主要参数如表1、表2所示，作业水深1 500m，系泊点布置如图1所示。

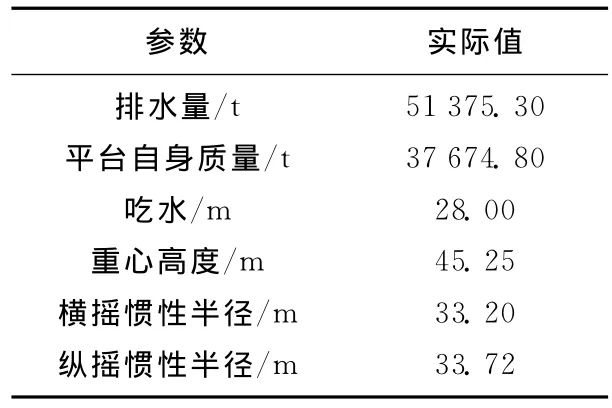
表1 TLP主要参数

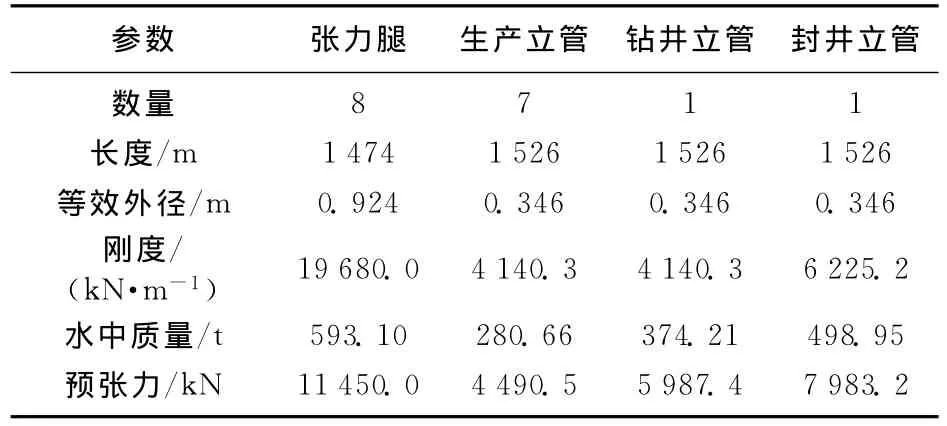
表2 TLP系泊系统及立管参数

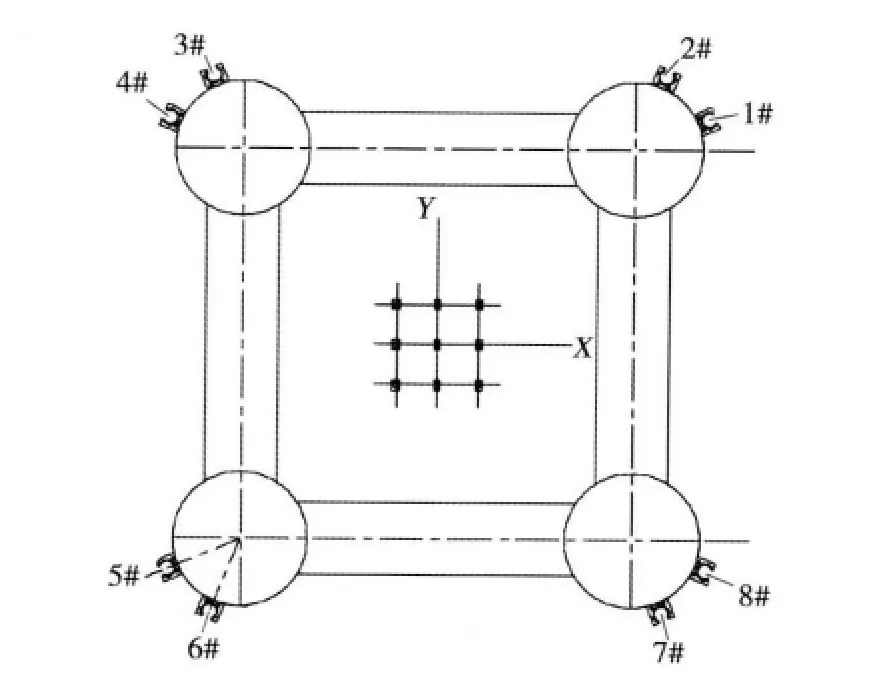
图1 TLP系泊点布置

2 静力特性分析

TLP采用垂直张紧式系泊系统，平台浮力值大于平台浮体重力，差值由张力腿及立管的预张力提供，系泊系统始终处于张紧状态。由于TLP系泊系统的特殊性，在平台发生水平偏移时，张力腿伸长，轴向力增加，继而使平台产生垂向位移。在计算其静力特性时，除了需考虑重力等引起的张力腿弯曲变形外，还需耦合考虑平台浮体的垂向位移。正是由于传统的系泊系统计算软件无法对垂直张紧式系泊系统进行计算，而综合水动力分析软件则较为耗时，因此提出了一种较为简化的方法计算垂直张紧式系泊系统的静力特性。

2.1 静力平衡方程

TLP系泊系统单位长度系泊缆的受力情况如图2所示，其静力平衡方程［5-6］为

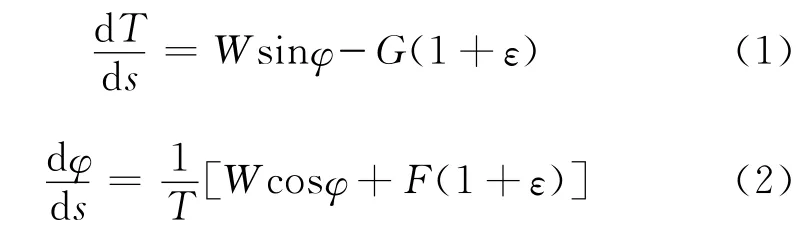
式（1）、（2）中：W为单位长度系泊缆重力；T为缆中张力；φ为倾角；ε为系泊缆单位长度的伸长量；G、F分别为单位长度切向及法向的流体作用力，G=CTρD（vccosφ）2／2，F=CNρD（vcsinφ）2／2，其中ρ为海水密度，D为系泊缆等效直径，vc为流速，CN、CT均为系数（对于圆形缆索，CN=1.2，CT=CN（d＋e／cosφ），d=-0.035，e=-0.035）。

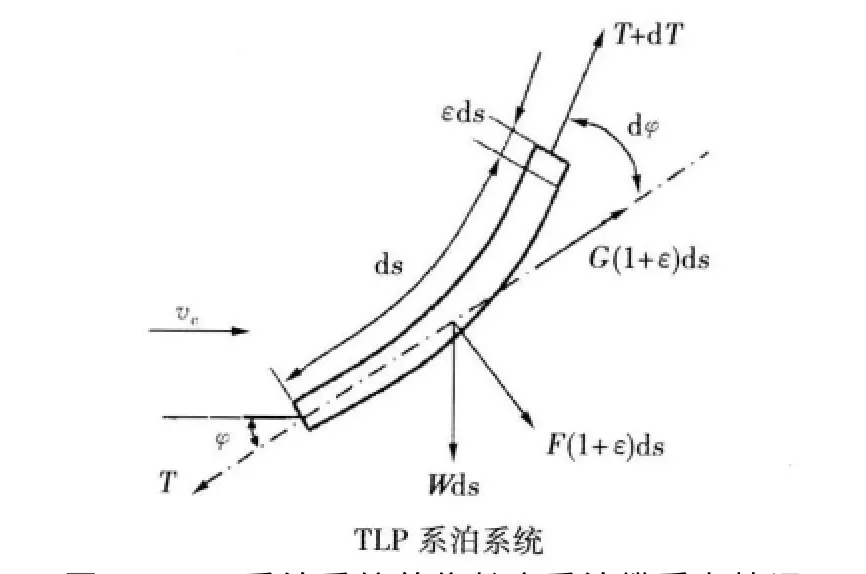
图2 TLP系泊系统单位长度系泊缆受力情况

从几何关系可以得到

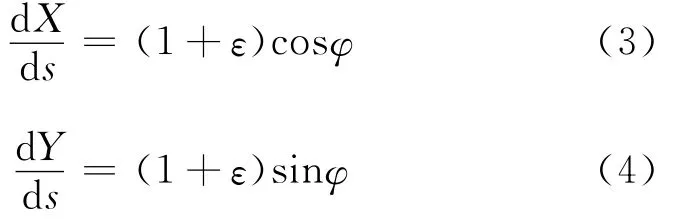
平台的静力平衡方程为

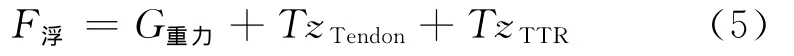
以平衡位置作为参考点

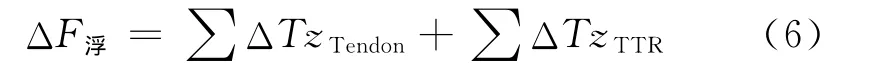
式（6）中：ΔF浮=ρAW·Δz，AW为平台水线面面积，Δz为吃水变化值；ΔTzTendon和ΔTzTTR分别为张力腿及立管中张力垂向分量相对于预张力的变化值。

2.2 求解方法

给定TLP的垂向位移，可通过式（6）计算得到张力腿及立管中张力垂向分量的增值。由于张力腿及立管初始倾角为90°，平台发生水平位移后其顶端倾角仍然接近垂直，因此可作如下近似假设：平台发生偏移后张力腿（立管）的轴向形变增量相同，张力腿（立管）的垂向刚度近似等于其轴向刚度，张力腿（立管）张力的垂向增量按其刚度比例分配。由此即可得到对应给定的垂向位移Δz时，每根张力腿及立管中张力的垂向分量值Tz。

再任意给定单根张力腿（立管）中顶端张力的横向分量值Tx，即可得到此根张力腿（立管）中的顶端张力及倾角。

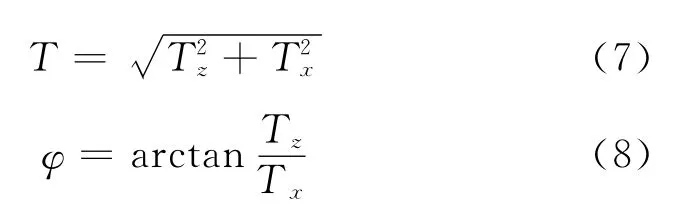
将式（7）、（8）代入式（1）～（4）进行积分，即可求得各项值。需要说明的是，积分中张力腿（立管）的总长度S为其不受力时的原长，而非处于初始平衡位置时的长度，即

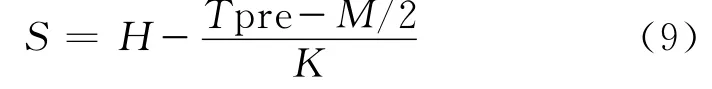
式（9）中：H为初始平衡位置时张力腿（立管）长度；Tpre为预张力；M为张力腿在水中重力；K为刚度。

控制条件为张力腿（立管）的垂向长度为其导缆孔距离海底的垂向距离，即Y=H-Δz。通过迭代，可求出符合条件的Tx值，继而求得对应的水平跨距X、顶端倾角φ、顶端张力T。

用上述方法对每根张力腿（立管）进行迭代计算，求得对应的Tx、X、φ、T。理论上，计算得到每根张力腿（立管）的跨距X应相等，可据此检验结果的正确性。由于近似的原因，计算结果表明张力腿与立管跨距X几乎相等，相对误差在1%之内。将所有张力腿与立管的Tx迭加即可求得此时的水平恢复力。

2.3 计算结果与分析

采用上述静力求解方法编程进行计算，得到张力腿平台水平恢复力与偏移的对应关系，并与用TLP模型刚度试验结果进行比较，以确定给出的系泊系统静力特性求解的准确性。

图3、4分别为TLP系泊系统水平恢复力和垂向偏移计算结果与模型试验测量结果对比图，可以看出静力计算结果与模型试验测量值吻合良好。TLP试验模型采用多根铝管与弹簧连接而成，虽然可准确模拟其水中外形、重力、轴向刚度等关键物理特性，但实际值与理论模型相比终究会存在一些差异，从而造成计算结果与试验测量结果之间的小量误差。经测算，水平位移80m内，水平恢复力的计算结果与模型试验测量结果的相对误差不超过5%。

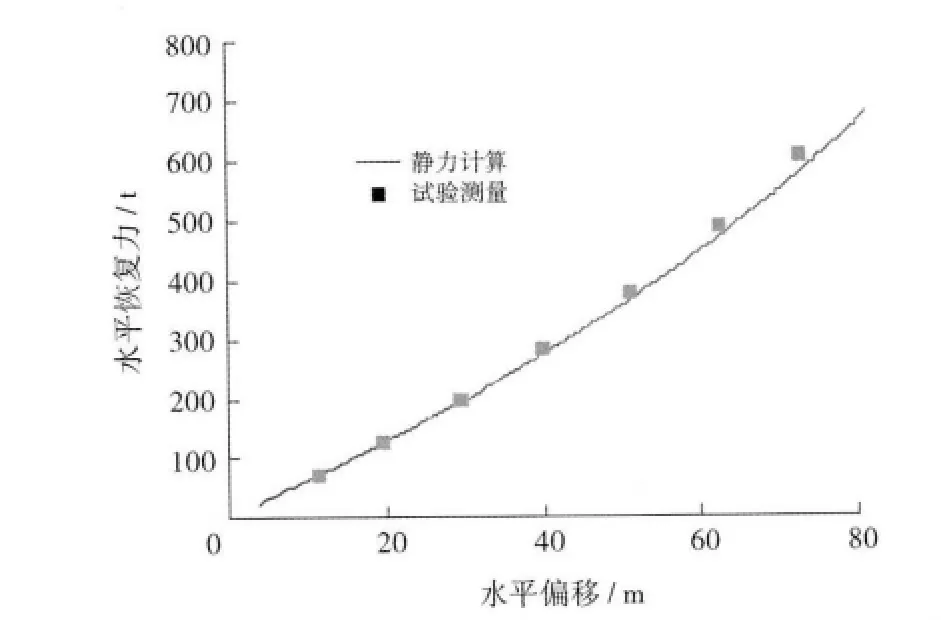
图3 TLP系泊系统水平恢复力计算与模型试验结果对比

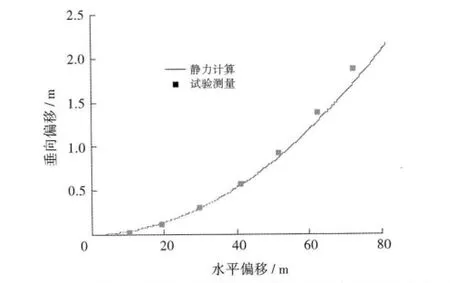
图4 TLP系泊系统平台垂向偏移计算与模型试验结果对比

3 动力特性分析

3.1 计算理论

TLP及张力腿（立管）的空间离散有限元模型动平衡方程［7］可表示为

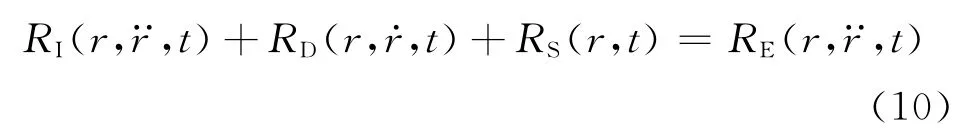
式（10）中：RI、RD和RS分别为惯性力、阻尼力和内部作用力；RE为外部激振力，包括重力、浮力、波浪激励力等；r··、r·、r分别为运动的加速度、速度和位移。

在进行耦合分析时，采用动态时域积分，将平台主体和系泊、立管系统看作整体的分析对象，在每一时间步中同时进行求解，每一步分析中都采用迭代求解的方法求出在该运动状态下的力学特征。耦合求解同时考虑平台主体对系泊、立管系统的影响，以及系泊、立管系统对平台主体的影响。

采用挪威船级社的Sesam软件进行分析。首先建立包含系泊系统的TLP三维模型（图5），在HydroD模块中对TLP进行频域计算，得到不同波频组合的平台运动及波浪激励力的传递函数，再将相关结果导入DeepC模块中进行时域耦合分析。所采用海况为南海一年一遇风浪流环境，如表3所示。

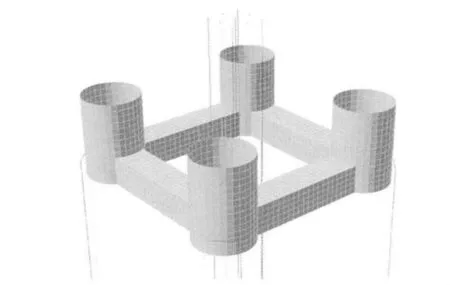
图5 TLP三维模型图

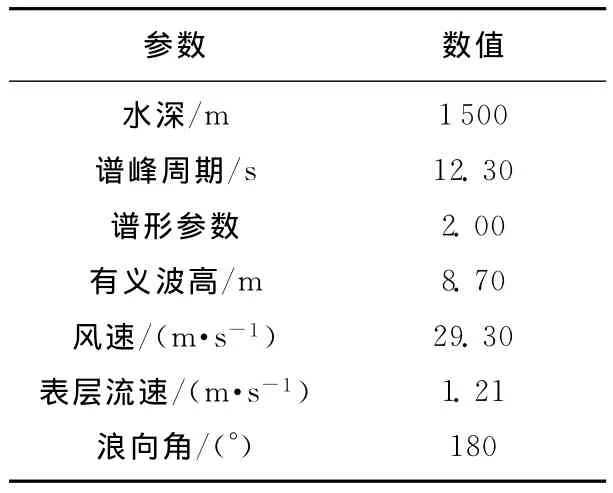
表3 南海一年一遇海况条件

3.2 计算结果与分析

TLP运动及张力腿张力的统计特性与试验值统计结果如表4所示。张力腿张力最大值出现在4＃张力腿，故对其进行分析。

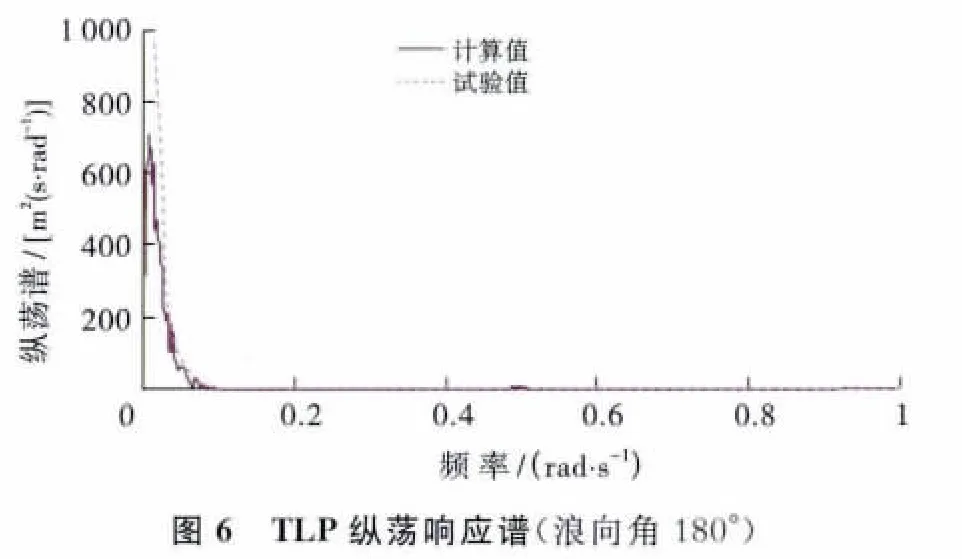
采用响应谱密度分析方法直观地显示出平台运动及张力腿动力响应的能量分布情况，并将计算结果与模型试验结果相对比，结果如图6～9所示。

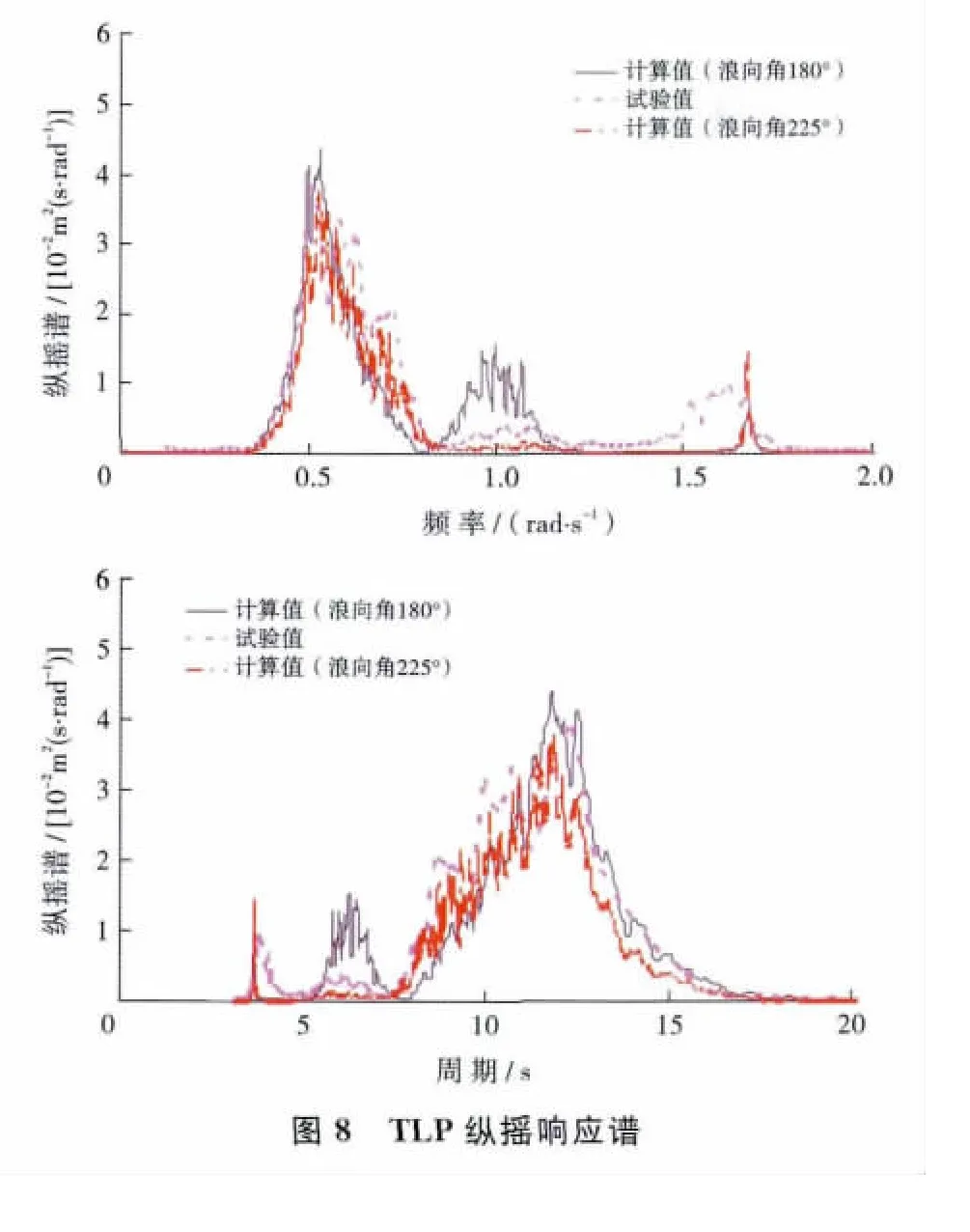
需要说明的是，试验测定条件为180°迎浪角，但由于张力腿刚度误差的不对称性，平台在发生较大水平位移之后的实际迎浪角存在小量的不确定性，而迎浪角对平台纵摇影响较大，故给出180°及225°迎浪角的纵摇计算值进行综合对比。

从图6～9可以看出：

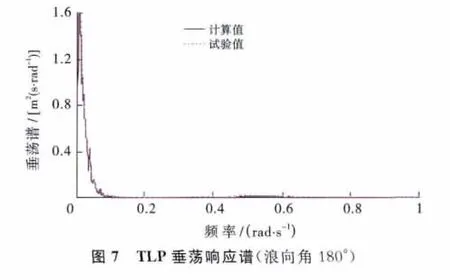
（1）TLP纵荡响应主要表现为低频响应，计算值与试验值相吻合。纵荡响应谱能量集中于0.1rad／s以下的低频区域，在0.5rad／s附近出现了一个较小的谱峰值，这是由于波谱在该频率下达到峰值所致。

（2）TLP垂荡响应受纵荡响应直接影响，故其谱形与纵荡谱形相似，表现为低频响应，计算值与试验值亦吻合。

（3）TLP纵摇响应主要表现为波频响应，其主峰值在0.5rad／s附近，对应谱峰周期为12.3s。在1.0rad／s附近出现第二个峰值，这主要由浪向角决定的，其对应纵摇RAO曲线的峰值在180°浪向角时其较为明显。在试验中由于张力腿刚度误差的不对称性，实际艏摇值大于计算值，因此实际浪向角介于180°与225°之间，试验值所测定的谱峰值介于180°与225°计算值之间，可认为其相吻合。在1.7rad／s附近出现的第三个峰值对应平台纵摇的固有频率，试验值相对计算值体现出更明显的高频响应。

表4 TLP运动及张力腿张力计算与试验统计结果

（4）TLP张力腿最大顶端张力出现在4＃张力腿，在全部时历中其最大值为20 100kN，平均值13 300kN，其主要谱形对应于纵摇谱形，主要表现为波频响应，亦有低频及高频成分，谱分析试验值与计算值基本吻合。

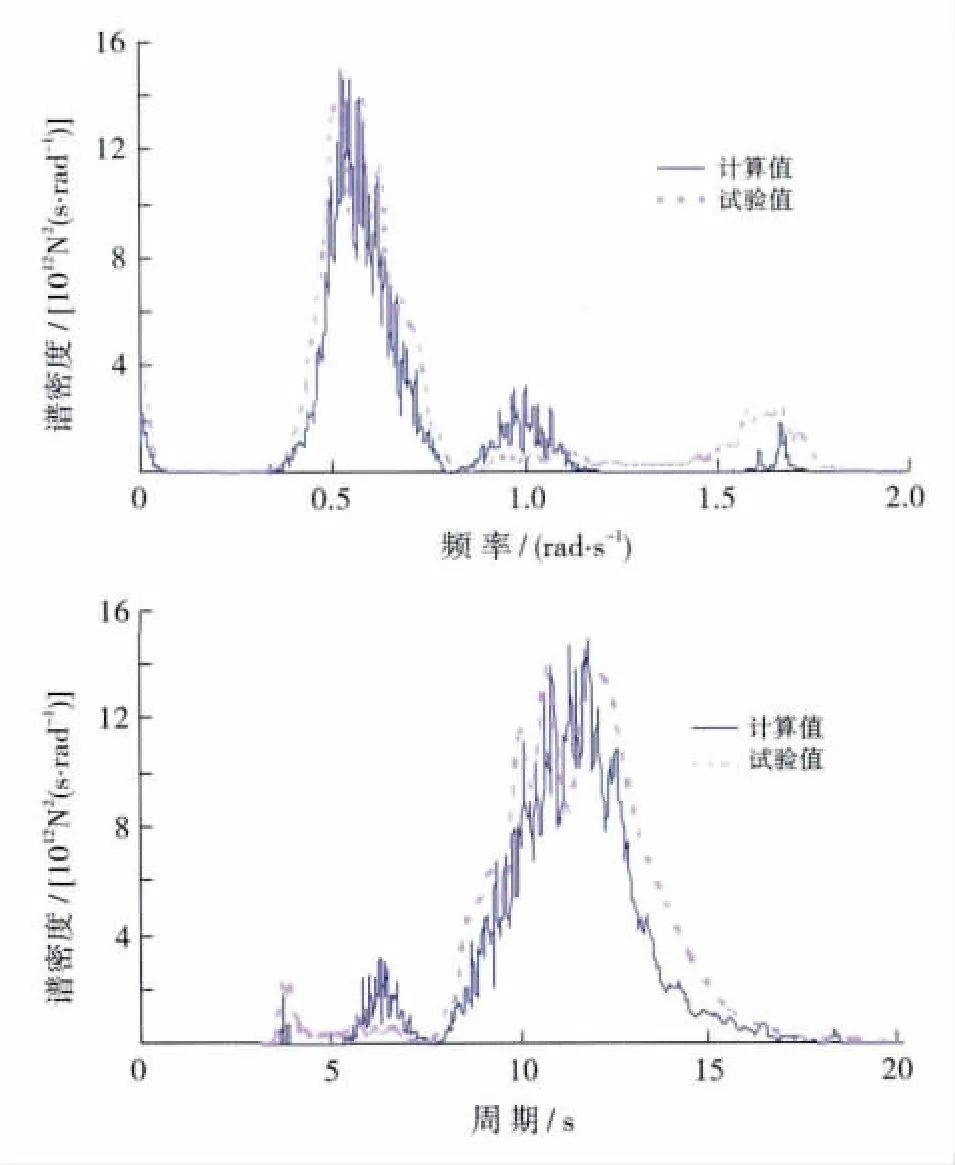
图9 TLP 4＃张力腿顶端张力谱（浪向角180°）

4 结论

（1）在静力方面，文中提出的TLP系泊系统简化分析方法计算结果与试验结果吻合较好，该方法可作为一种快速评估张力腿静力特性的手段，对平台设计前期方案筛选有较大帮助，可节省人力与时间。

（2）在动力方面，通过数值分析与模型试验的结果对比可以看出，由于TLP采用垂直张紧式系泊系统，其垂荡运动受水平运动的直接影响，张力腿张力平均值对应于平台水平方向的偏移，对应关系体现为静力特性；而从谱分析对比可以看出，180°浪向角时张力腿张力变化幅值主要由纵摇运动确定，主要体现为波频响应。

（3）由于试验所测得高频响应部分要比计算值更为明显，因此对于TLP张力腿高频响应部分的预报需要进一步探讨。

［1］ALBERTO F.Reliability of TLP tethers using evolutionary strategies［C］.Proceedings of the ASME 27th International Conference on Offshore Mechanics and Arctic Engineering，2008.

［2］JAYALEKSHMI R，IDICHANDY V G，SUNDARAVADIVELU R.Physical simulation of the hull-tether coupled dynamics of a deepwater TLP［C］.Proceedings of the 26th International Conference on Offshore Mechanics and Arctic Engineering，2007.

［3］CHAN K Y，KIM MH.Transient effects of tendon disconnection of a TLP by hull-tendon-riser coupled dynamic analysis［J］.Ocean Engineering，2010，37：667-677.

［4］XIAO Q B，LEVERETTE S J，RIJKEN O R.A TLP solution for 8000ft water depth［C］.Proceedings of the ASME 2010 29th International Conference on Ocean，2010.

［5］潘斌，高捷.浮标系泊系统静力计算［J］.重庆交通学院学报，1997，16（1）：68-73.

［6］张火明，范菊，杨建民.深水系泊系统静力特性快速计算方法研究［J］.船海工程，2007，36（2）：64-68.

［7］童波，杨建民，李欣.深水半潜平台系泊系统动力特性研究［J］.海洋工程，2009，27（1）：1-7.